Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Ta có $y' = \cos x \Rightarrow y' = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$
Do $x\in \left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ nên $k=-1$ hay $x=-\dfrac{\pi }{2}$
Suy ra $y\left( { - \dfrac{\pi }{2}} \right) = - 1;\;\;y\left( { - \dfrac{\pi }{3}} \right) = - \dfrac{{\sqrt 3 }}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{\mathop {\max}\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]}y = - \dfrac{{\sqrt 3 }}{2}}\\{{\rm{ \;}}}&{\mathop {\min }\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]} y = - 1}\end{array}} \right.$
Công ty sữa Vinamilk thiết kế các sản phẩm dạng hình hộp chữ nhật có đáy là hình chữ nhật có chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Sản phẩm chứa dung tích bằng \(180{\rm{ml}}\). Khi thiết kế công ty luôn đặt ra mục tiêu sao cho vật liệu làm vỏ hộp là tiết kiệm nhất. Để công ty tiết kiệm được vật liệu nhất thì chiều dài của đáy hộp gần bằng giá trị nào sau đây?
Bước 1: Gọi chiều dài của đáy hộp là \(x(\;{\rm{cm}}),x > 0\), chiều cao của hộp chữ nhật là \(h(\;{\rm{cm}}),h > 0\).
Ta có \(180ml = 180\;c{m^3}\).
Gọi chiều dài của đáy hộp là \(x(\;{\rm{cm}}),x > 0\), chiều cao của hộp chữ nhật là \(h(\;{\rm{cm}}),h > 0\).
Chiều rộng của đáy hộp là \(\dfrac{2}{3}x(\;{\rm{cm}})\).
Ta có thể tích của khối hộp chữ nhật là \(V = x \cdot \dfrac{2}{3}x.h = 180\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)\( \Rightarrow h = \dfrac{{270}}{{{x^2}}}(\;{\rm{cm}})\).
Bước 2: Tính giá trị nhỏ nhất của diện tích toàn phần của khối hộp chữ nhật theo x.
Diện tích toàn phần của khối hộp chữ nhật là
\(f(x) = {S_{TP}} = 2 \cdot x \cdot \dfrac{2}{3}x + 2 \cdot x \cdot \dfrac{{270}}{{{x^2}}}\)\( + 2 \cdot \dfrac{2}{3}x \cdot \dfrac{{270}}{{{x^2}}}\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\)\( = \dfrac{4}{3}{x^2} + \dfrac{{900}}{x}\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\)
Yêu cầu bài toán trở thành tìm \(x\) dương để hàm số \(f(x) = \dfrac{4}{3}{x^2} + \dfrac{{900}}{x}\) đạt giá trị nhỏ nhất.
Áp dụng bất đẳng thức Cô-si cho 3 số dương \(\dfrac{4}{3}{x^2},\dfrac{{450}}{x},\dfrac{{450}}{x}\) ta có
\(\mathop 3\limits^4 {x^2} + \dfrac{{450}}{x} + \dfrac{{450}}{x}\)\( \ge 3\sqrt[3]{{\dfrac{4}{3}{x^2} \cdot \dfrac{{450}}{x} \cdot \dfrac{{450}}{x}}}\)\( \Leftrightarrow f(x) \ge 3\sqrt[3]{{270000}},\forall x > 0\)
Dấu "=" xảy ra khi và chỉ khi \(\dfrac{4}{3}{x^2} = \dfrac{{450}}{x} = \dfrac{{450}}{x}\)\( \Leftrightarrow x = \dfrac{{\sqrt[3]{{2700}}}}{2} \approx 6,96(\;{\rm{cm}})\).
Gọi \(m\) và \(M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = x - \sqrt {4 - {x^2}} .\) Khi đó \(M + m\) bằng
Ta có: \(y = x - \sqrt {4 - {x^2}} \)
TXĐ: \(D = \left[ { - 2;\,\,2} \right].\)
\(\begin{array}{l} \Rightarrow y' = 1 + \dfrac{x}{{\sqrt {4 - {x^2}} }} \Rightarrow y' = 0\\ \Leftrightarrow x + \sqrt {4 - {x^2}} = 0 \Leftrightarrow \sqrt {4 - {x^2}} = - x\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\{x^2} = 4 - {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\{x^2} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\end{array} \right. \Leftrightarrow x = - \sqrt 2 \\ \Rightarrow \left\{ \begin{array}{l}y\left( 2 \right) = 2\\y\left( { - \sqrt 2 } \right) = - 2\sqrt 2 \\y\left( { - 2} \right) = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} y = y\left( 2 \right) = 2\\m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} y = y\left( { - \sqrt 2 } \right) = - 2\sqrt 2 \end{array} \right.\\ \Rightarrow M + m = 2 - 2\sqrt 2 .\end{array}\)
Cho hàm số \(f\left( x \right) = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\). Gọi \(M\) là giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 1;3} \right]\). Tổng các giá trị của tham số thực \(m\) để \(M = \dfrac{{71}}{2}.\)
Đặt \(h\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2} + m\) ta có:
\(h'\left( x \right) = 12{x^3} - 12{x^2} - 24x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
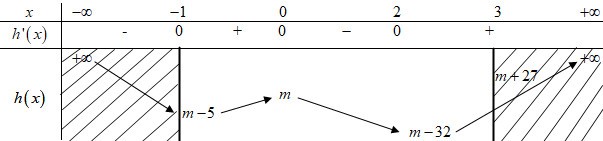
Ta thấy \(m - 32 < m - 5 < m < m + 27\).
TH1: \(m - 32 \ge 0 \Leftrightarrow m \ge 32\).
\( \Rightarrow M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\left( {ktm} \right)\).
TH2: \(m - 32 < 0 \le m - 5 \Leftrightarrow 5 \le m < 32\).
\( \Rightarrow M \in \left\{ {32 - m;m + 27} \right\}\).
Nếu \(m + 27 \ge 32 - m \Leftrightarrow 2m \ge 5 \Leftrightarrow m \ge \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow 5 \le m < 32\), khi đó \(M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\,\left( {tm} \right)\).
Nếu \(m + 27 < 32 - m \Leftrightarrow m < \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow m \in \emptyset \).
TH3: \(m - 5 < 0 \le m \Leftrightarrow 0 \le m < 5\).
\( \Rightarrow M \in \left\{ {32 - m;m + 27} \right\}\).
Nếu \(m + 27 \ge 32 - m \Leftrightarrow 2m \ge 5 \Leftrightarrow m \ge \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow \dfrac{5}{2} \le m < 5\), khi đó \(M = m + 27 = \dfrac{{71}}{2} \Leftrightarrow m = \dfrac{{17}}{2}\,\,\,\left( {ktm} \right)\).
Nếu \(m + 27 < 32 - m \Leftrightarrow m < \dfrac{5}{2}\), kết hợp điều kiện \( \Rightarrow 0 \le m < \dfrac{5}{2}\), khi đó \(M = 32 - m = \dfrac{{71}}{2} \Leftrightarrow m = - \dfrac{7}{2}\,\,\left( {ktm} \right)\).
TH4: \(m + 27 \le 0 \Leftrightarrow m \le - 27\), khi đó \(M = 32 - m = \dfrac{{71}}{2} \Leftrightarrow m = - \dfrac{7}{2}\,\,\,\left( {tm} \right)\).
Vậy có hai giá trị của \(m\) thỏa mãn yêu cầu bài toán là \(m \in \left\{ {\dfrac{{17}}{2}; - \dfrac{7}{2}} \right\}\), tổng các giá trị của \(m\) là \(\dfrac{{17}}{2} + \left( { - \dfrac{7}{2}} \right) = \dfrac{{10}}{2} = 5\).
Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán mỗi kg là \(40\;000\) đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng \(30\;{\rm{kg}}\). Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 4000 đồng thì số vải thiều bán được tăng thêm là \(40\;{\rm{kg}}\). Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kilôgam là 25000 đồng.
Bước 1:
Gọi \(x\) (đồng) là giá bán thực tế của mỗi kilôgam vải thiều \((25000 \le x \le 40000)\).
Bước 2: Biểu diễn số \({\rm{kg}}\) vải thiều bán được tương ứng với giá bán \(x\)
Theo bài ra số kilôgam bán thêm được là: \((40000 - x) \cdot \dfrac{{40}}{{4000}} = \dfrac{1}{{100}}(40000 - x)\).
Do đó số \({\rm{kg}}\) vải thiều bán được tương ứng với giá bán \(x\) :
\(30 + \dfrac{1}{{100}}(40000 - x)\)\( = - \dfrac{1}{{100}}x + 430\).
Gọi \(F(x)\) là hàm lợi nhuận thu được \((F(x)\) : đồng).
Ta có:
\(\begin{array}{l}F(x) = \left( { - \dfrac{1}{{100}}x + 430} \right) \cdot (x - 25000)\\ = - \dfrac{1}{{100}}{x^2} + 680x - 10750000\end{array}\).
Bước 3: Tìm giá trị lớn nhất của hàm lợi nhuận \(F(x)\) trên $[25000 ; 40000]$.
Bài toán trở thành tìm giá trị lớn nhất của
\(F(x) = - \dfrac{1}{{100}}{x^2} + 680x - 10750000\) trên $[25000 ; 40000]$.
Ta có: \({F^\prime }(x) = - \dfrac{1}{{50}}x + 680.\)
\({F^\prime }(x) = 0\)\( \Leftrightarrow - \dfrac{1}{{50}}x + 680 = 0 \Leftrightarrow x = 34000\).
Vì hàm \(F(x)\) liên tục trên đoạn $[25000 ; 40000]$ nên ta có:
\(F(25000) = 0;F(34000) = 810000;\)\(F(40000) = 450000.{\rm{ }}\)
Vậy với \(x = 34000\) thì \(F(x)\) đạt giá trị lớn nhất.
Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi kg vải thiều là 34000 đồng.
Trên đoạn [1 ; 5], hàm số \(y = x + \dfrac{4}{x}\) đạt giá trị nhỏ nhất tại điểm
Cách 1. Hàm số \(y = f(x) = x + \dfrac{4}{x}\) xác định trên đoạn [1 ; 5].
Ta có: \(y' = 1 - \dfrac{4}{{{x^2}}}\)
\({y^\prime } = 0 \Leftrightarrow 1 - \dfrac{4}{{{x^2}}} = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 \in [1;5]}\\{x = - 2 \notin [1;5]}\end{array}} \right.\)
\(f\left( 1 \right) = 5;\) \(f(5) = \dfrac{{29}}{5};f(2) = 4\)
Vậy GTNN của hàm số là 4 đạt tại \(x = 2\).
Cách 2. Áp dụng BĐT Cô si cho hai số dương \(x;\dfrac{4}{x}\) ta được:
\(x + \dfrac{4}{x} \ge 2\sqrt {x.\dfrac{4}{x}} = 4\)
Dấu “=” xảy ra khi và chỉ khi \(x = \dfrac{4}{x} \Leftrightarrow x = 2\)
Đề thi THPT QG 2019 – mã đề 104
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 3x\) trên đoạn \(\left[ { - 3;3} \right]\) bằng
Hàm số \(f\left( x \right) = {x^3} - 3x\) xác định trên \(\mathbb{R}\) nên xác định trên \(\left[ { - 3;3} \right]\).
Ta có \(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1 \in \left[ { - 3;3} \right]\).
\(f\left( { - 3} \right) = - 18;\,\,f\left( 3 \right) = 18;\,\,f\left( { - 1} \right) = 2;\,\,f\left( 1 \right) = - 2\).
Vậy \(\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = f\left( { - 3} \right) = - 18\).
Đề thi THPT QG - 2021 - mã 103
Trên đoạn \(\left[ {0;3} \right]\), hàm số \(y = {x^3} - 3x + 4\) đạt giá trị nhỏ nhất tại điểm
Khảo sát hàm số \(y = {x^3} - 3x + 4\) trên \(\left[ {0;3} \right]\).
+ \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = {\kern 1pt} \pm 1\).
+ BBT:
\( \Rightarrow \) Hàm số đạt giá trị nhỏ nhất tại \(x = 1\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị bên. Gọi \(M,m\) lần lượt là giá trị lớn nhất và nhỏ nhất của đồ thị hàm số đã cho trên đoạn \(\left[ { - 2;2} \right]\). Giá trị của \(M + m\) bằng
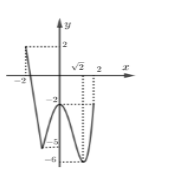
Từ đồ thị hàm số, xét trên đoạn \(\left[ { - 2;2} \right]\) ta thấy giá trị lớn nhất của hàm số là \(y = 2 \Leftrightarrow x = - 2\) và giá trị nhỏ nhất của hàm số là \(y = - 6 \Leftrightarrow x = \sqrt 2 \).
Suy ra \(M = 2;\,\,m = - 6\) nên \(M + m = 2 + \left( { - 6} \right) = - 4\).
Có bao nhiêu giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \dfrac{{x - {m^2} - 2}}{{x - m}}\) trên đoạn \(\left[ {0;\,4} \right]\) bằng \( - 1.\)
ĐK : \(x \ne m\)
Ta có \(y' = \dfrac{{{m^2} - m + 2}}{{{{\left( {x - m} \right)}^2}}}\) nhận thấy\({m^2} - m + 2 = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{7}{4} > 0;\,\forall m\) nên \(y' > 0;\,\forall m\)
Hay hàm số đồng biến trên từng khoảng xác định.
Để hàm số đạt GTLN trên \(\left[ {0;4} \right]\) thì \(m \notin \left[ {0;4} \right] \Leftrightarrow \left[ \begin{array}{l}m < 0\\m > 4\end{array} \right.\)
Suy ra \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y\left( 4 \right) = \dfrac{{4 - {m^2} - 2}}{{4 - m}}\,\) . Theo bài ra ta có
\(\dfrac{{4 - {m^2} - 2}}{{4 - m}} = - 1 \) \(\Rightarrow - {m^2} + 2 = m - 4 \Leftrightarrow {m^2} + m - 6 = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\left( {ktm} \right)\\m = - 3\,\,\left( {tm} \right)\end{array} \right.\)
Vậy có một giá trị của \(m\) thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;3} \right]\). Giá trị của \(M - m\) bằng
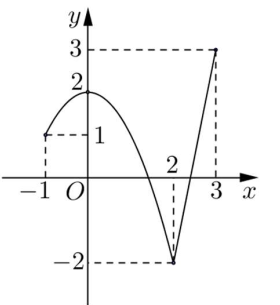
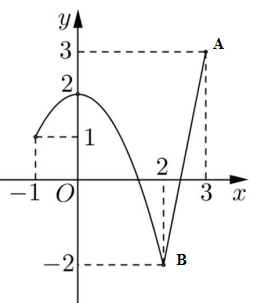
Từ đồ thị hàm số ta thấy trên đoạn \(\left[ { - 1;3} \right]\) thì điểm cao nhất của đồ thị là điểm \(A\left( {3;3} \right)\) và điểm thấp nhất của đồ thị là \(B\left( {2; - 2} \right)\) nên GTLN của hàm số là \(M = 3\) và GTNN của hàm số là \(m = - 2.\)
Từ đó \(M - m = 3 - \left( { - 2} \right) = 5.\)
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Nếu $M = - 2$ là GTLN của hàm số $y = f\left( x \right)$ trên $\left[ {1;3} \right]$ thì $f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$.
Đề thi THPT QG – 2021 lần 1– mã 104
Trên đoạn \(\left[ { - 1;2} \right],\) hàm số \(y = {x^3} + 3{x^2} + 1\) đạt giá trị nhỏ nhất tại điểm
Ta có: \(y' = 3{x^2} + 6x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\, \in \left[ { - 1;2} \right]\\x = -2\, \notin \left[ { - 1;2} \right]\end{array} \right.\)
\(y\left( { - 1} \right) = 3;\,\,y\left( 0 \right) = 1\,\,;\,y\left( 2 \right) = 21\)
Hàm số đạt giá trị nhỏ nhất tại điểm \(x = 0\).
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
TXĐ: $x \ne 0$.
$f'\left( x \right) = \dfrac{{x\cos x - \sin x}}{{{x^2}}} < 0 \forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$
Thật vậy,
Xét hàm \(g\left( x \right) = x\cos x - \sin x\) trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\) có:
\(g'\left( x \right) = \cos x - x\sin x - \cos x\) \( = - x\sin x < 0,\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
Do đó hàm số \(g\left( x \right)\) nghịch biến trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\).
Suy ra \(g\left( x \right) \le g\left( {\dfrac{\pi }{6}} \right)\) \( = \dfrac{\pi }{6}.\cos \dfrac{\pi }{6} - \sin \dfrac{\pi }{6} < 0\) hay \(x\cos x - \sin x < 0\) với \(\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
$ \Rightarrow \mathop {\max }\limits_{\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]} f\left( x \right) = f\left( {\dfrac{\pi }{6}} \right) = \dfrac{3}{\pi }$.
Cho hàm số \(y = {x^2}\), biết \({x^2} \ge 0,\forall x \in R\) và \({x^2} = 0 \Leftrightarrow x = 0 \Rightarrow y = 0\). Khi đó \(y = 0\) là:
\(y = 0\) là GTNN của hàm số
Cho hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - 3;7} \right)\) và xác định tại hai điểm \(x = - 3;x = 7\). Chọn kết luận đúng:
Vì hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - 3;7} \right)\) và tồn tại \(f\left( { - 3} \right),f\left( 7 \right)\) nên \(f\left( { - 3} \right) < f\left( x \right) < f\left( 7 \right),\forall x \in \left[ { - 3;7} \right]\).
Vậy \(f\left( { - 3} \right)\) là GTNN của \(f\left( x \right)\) trên \(\left[ { - 3;7} \right]\).
Gọi $M,{\rm{ }}m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $f\left( x \right) = \dfrac{{x + 1}}{{x - 1}}$ trên $\left[ {3;5} \right]$. Khi đó $M - m$ bằng
Xét hàm số $f\left( x \right) = \dfrac{{x + 1}}{{x - 1}}$ trên $\left[ {3;5} \right],$ có $f'\left( x \right) = - \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} < 0;{\mkern 1mu} {\mkern 1mu} \forall x \in \left[ {3;5} \right].$
Suy ra $f\left( x \right)$ là hàm số nghịch biến trên [3;5]
=>\(M=f(3)=2,m=f(5)=\dfrac{3}{2}\)
=>\(M-m=\dfrac{1}{2}\)
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = + \infty \). Khi đó:
Vì \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = + \infty \) nên không tồn tại số \(M\) để \(f\left( x \right) \le M,\forall x \in \left( {a;b} \right)\), do đó hàm số không có GTLN trên \(\left( {a;b} \right)\)
Để giá trị nhỏ nhất của hàm số $y = x + \dfrac{1}{x} - m$ trên khoảng $\left( {0; + \infty {\rm{\;}}} \right)$ bằng $ - 3$ thì giá trị của tham số $m$ là:
$x + \dfrac{1}{x} - m\mathop \ge \limits^{Cauchy} {\mkern 1mu} 2\sqrt {x.\dfrac{1}{x}} - m = 2 - m$$ \Rightarrow \mathop {\min }\limits_{\left( {0; + \infty {\rm{\;}}} \right)} {\mkern 1mu} y = 2 - m = - 3 \Leftrightarrow m = 5$
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
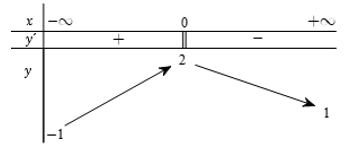
Khẳng định nào sau đây là đúng?
Dựa vào bảng biến thiên nhận thấy:
+) \(f\left( x \right) \le 2,\,\,\forall x \in \mathbb{R}\) và \(f\left( 0 \right) = 2\) nên GTLN của hàm số bằng \(2.\)
+) \(f\left( x \right) \ge - 1,{\rm{ }}\forall x \in \mathbb{R}\) và vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) nên không tồn tại \({x_0} \in \mathbb{R}\) sao cho \(f\left( {{x_0}} \right) = 1\), do đó hàm số không có GTNN.

