Cho tứ diện $ABCD $ và $G$ là trọng tâm tam giác $ACD.$ Mặt phẳng $(P)$ qua $BG$ và song song với $CD$ chia khối tứ diện thành hai phần. Tính tỉ số thể tích (số bé chia số lớn) của hai phần đó là:
Gọi $H$ là trung điểm của $CD.$ Ta có $G$ là trọng tâm tam giác $ACD$ \( \Rightarrow \dfrac{{AG}}{{AH}} = \dfrac{2}{3}.\)
Trong mặt phẳng $ACD,$ qua $G$ kẻ đường thẳng song song với $CD,$ cắt $AC$ tại $M$ và cắt $AD$ tại $N.$
Khi đó ta có mặt phẳng (P) là mặt phẳng (BMN).
Mặt phẳng (BMN) chia tứ diện ABCD thành hai phần là ABMN có thể tích
\({V_1}\) và BMNDC có thể tích \({V_2}.\)
\( \Rightarrow V = {V_{ABCD}} = {V_1} + {V_2}.\)
Ta có MN//CD theo cách dựng \( \Rightarrow \dfrac{{AM}}{{AC}} = \dfrac{{AN}}{{AD}} = \dfrac{{AG}}{{AH}} = \dfrac{2}{3}\) (định lý Ta-lét).
Theo công thức tỉ lệ thể tích ta có: \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \dfrac{{{V_1}}}{V} = \dfrac{{AB}}{{AB}}.\dfrac{{AM}}{{AC}}.\dfrac{{AN}}{{AD}} = \dfrac{2}{3}.\dfrac{2}{3} = \dfrac{4}{9}.\)
\(\begin{array}{l} \Rightarrow {V_1} = \dfrac{4}{9}V \Rightarrow {V_2} = V - {V_1} = \dfrac{5}{9}V.\\ \Rightarrow {V_1} < {V_2} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{4}{9}.\dfrac{9}{5} = \dfrac{4}{5}.\end{array}\)
Cho hình chóp $S.ABC$ có $AB = 5cm,\;BC = 6cm,\;CA = 7cm$. Hình chiếu vuông góc của $S$ xuống mặt phẳng $\left( {ABC} \right)$ nằm bên trong tam giác $ABC$. Các mặt phẳng $\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)$ đều tạo với đáy một góc $60^\circ $. Gọi $AD,\;BE,\;CF$ là các đường phân giác của tam giác $ABC$ với $D \in BC,E \in AC,F \in AB$ .Thể tích $S.DEF$ gần nhất với số nào sau đây?
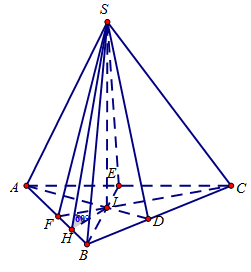
Vì các mặt phẳng $\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)$ đều tạo với đáy một góc $60^\circ $ và hình chiếu vuông góc của $S$ xuống mặt phẳng $\left( {ABC} \right)$ nằm bên trong tam giác $ABC$ nên ta có hình chiếu của $S$ xuống mặt phẳng $\left( {ABC} \right)$ là tâm đường tròn nội tiếp $I$ của tam giác $ABC$.
Gọi $p$ là nửa chu vi tam giác $ABC$ thì $p = \dfrac{{5 + 6 + 7}}{2} = 9$.
Ta có ${S_{ABC}} = \sqrt {9\left( {9 - 5} \right)\left( {9 - 6} \right)\left( {9 - 7} \right)} = 6\sqrt 6 $ và $r = \dfrac{S}{p} = \dfrac{{6\sqrt 6 }}{9} = \dfrac{{2\sqrt 6 }}{3}$
Chiều cao của hình chóp là: $h = r.\tan 60^\circ = 2\sqrt 2 $
Kí hiệu $BC = a,AC = b,AB = c$. Ta có:
Vì $BE$ là phân giác của góc $B$ nên ta có: $\dfrac{{AE}}{{CE}} = \dfrac{{BA}}{{BC}}$. Tương tự $\dfrac{{FA}}{{FB}} = \dfrac{{CA}}{{CB}},\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}$
Khi đó $\dfrac{{{S_{AEF}}}}{{{S_{ABC}}}} = \dfrac{{AE}}{{AC}}.\dfrac{{AF}}{{AB}} = \dfrac{{AB}}{{AB + BC}}.\dfrac{{AC}}{{AC + BC}}$, tương tự: $\dfrac{{{S_{CED}}}}{{{S_{ABC}}}} = \dfrac{{CA}}{{CA + AB}}.\dfrac{{CB}}{{CB + AB}}$,
$\dfrac{{{S_{BFD}}}}{{{S_{ABC}}}} = \dfrac{{BC}}{{BC + CA}}.\dfrac{{BA}}{{BA + CA}}$
Do đó
${S_{DEF}} = {S_{ABC}}.\left( {1 - \dfrac{{ab}}{{\left( {a + c} \right)\left( {b + c} \right)}} - \dfrac{{bc}}{{\left( {b + a} \right)\left( {c + a} \right)}} - \dfrac{{ac}}{{\left( {a + b} \right)\left( {c + b} \right)}}} \right) = \dfrac{{2abc}}{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}.{S_{ABC}} = \dfrac{{210\sqrt 6 }}{{143}}$
Suy ra: ${V_{S.DEF}} = \dfrac{1}{3}.\dfrac{{210\sqrt 6 }}{{143}}.2\sqrt 2 = \dfrac{{280\sqrt 3 }}{{143}}\,\left( {c{m^3}} \right) \approx 3,4\left( {c{m^3}} \right)$
Khối chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $SA = SB = SC = a$, cạnh $SD$ thay đổi. Thể tích khối chóp $S.ABCD$ lớn nhất khi độ dài cạnh $SD$ là:
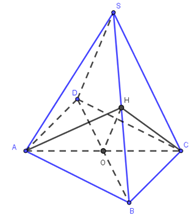
Khối chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $SA = SB = SC = a$
$ \Rightarrow $ Khối chóp $S.ABC$ có: $SA = SB = SC = BA = BC = a$ và có thể tích bằng $\dfrac{1}{2}$ thể tích khối chóp $S.ABCD.$
Như vậy, để thể tích khối chóp $S.ABCD$ lớn nhất thì thể tích khối chóp $S.ABC$ lớn nhất khi $SD $ thay đổi.
Gọi $H$ là trung điểm của $SB.$
$\Delta SAB,\,\,\Delta SBC$ là $2$ tam giác đều, cạnh $a$ $ \Rightarrow AH = CH = \dfrac{{a\sqrt 3 }}{2}$
Và $AH \bot SB,\,\,CH \bot SB \Rightarrow SB \bot (AHC) \Rightarrow BH \bot \left( {AHC} \right)$
\( \Rightarrow {V_{S.ABC}} = 2{V_{B.AHC}}\) \( = 2.\dfrac{1}{3}BH.{S_{AHC}}\) \( = 2.\dfrac{1}{3}.\dfrac{1}{2}SB.{S_{AHC}} = \dfrac{1}{3}a.{S_{AHC}}\)
Mặt khác ${S_{AHC}} = \dfrac{1}{2}.AH.CH.\sin \widehat {AHC} = \dfrac{1}{2}.{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2}\sin \widehat {AHC}$
$ \Rightarrow {V_{S.ABC}}$ lớn nhất khi và chỉ khi $\widehat {AHC} = {90^0} \Leftrightarrow AH \bot HC $ $\Rightarrow \Delta AHC$ vuông cân tại $H$ $ \Rightarrow HO = \dfrac{{AH}}{{\sqrt 2 }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt 2 }} = \dfrac{{a\sqrt 3 }}{{2\sqrt 2 }}$
$OH$ là đường trung bình của $\Delta SBD$ $ \Rightarrow SD = 2.OH = 2.\dfrac{{a\sqrt 3 }}{{2\sqrt 2 }} = \dfrac{{a\sqrt 3 }}{{\sqrt 2 }} = \dfrac{{a\sqrt 6 }}{2}$
Vậy, để thể tích khối chóp $S.ABCD$ lớn nhất khi độ dài cạnh $SD$ là: $\dfrac{{a\sqrt 6 }}{2}$.
Cho khối lăng trụ \(ABC.A'B'C',\) khoảng cách từ \(C\) đến đường thẳng \(BB'\) bằng \(\sqrt 5 ,\) khoảng cách từ \(A\) đến các đường thẳng \(BB'\) và \(CC'\) lần lượt bằng \(1\) và \(2,\) hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {A'B'C'} \right)\) là trung điểm \(M\) của \(B'C'\) và \(A'M = \sqrt 5 .\) Thể tích của khối lăng trụ đã cho bằng:
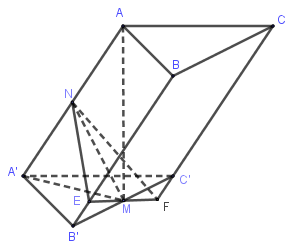
Qua \(M\) dựng mặt phẳng \(\left( P \right)\) vuông góc với \(AA'\) cắt các cạnh \(AA',\;BB',\;CC'\) lần lượt tại \(N,\;E,\;F.\)
Ta có: \(\left\{ \begin{array}{l}AA' \bot NE \Rightarrow NE = d\left( {E,\;AA'} \right) = d\left( {N,\;BB'} \right) = d\left( {A,\;BB'} \right) = 1.\\AA' \bot NF \Rightarrow NF = d\left( {F,\;AA'} \right) = d\left( {N,\;CC'} \right) = d\left( {A,\;CC'} \right) = 2\\AA' \bot \left( P \right) \Rightarrow CC' \bot \left( P \right) \Rightarrow CC' \bot EF \Rightarrow EF = d\left( {E,\;CC'} \right) = d\left( {F,\;BB'} \right) = d\left( {C,\;BB'} \right) = \sqrt 5 .\end{array} \right.\)
Có: \(N{E^2} + N{F^2} = EF{'^2} \Rightarrow \Delta NEF\) vuông tại \(N.\) (định lý Pi-ta-go đảo)
Mà: \(\dfrac{{ME}}{{MF}} = \dfrac{{MB'}}{{MC'}} = 1 \Rightarrow ME = MF\) (định lý Ta-lét)\( \Rightarrow M\) là trung điểm của \(EF.\)
\( \Rightarrow MN = \dfrac{1}{2}EF = \dfrac{{\sqrt 5 }}{2}.\)
Xét tam giác \(AA'M\) vuông tại \(M\) ta có:
\(\dfrac{1}{{M{N^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{A'{M^2}}} \Leftrightarrow \dfrac{4}{5} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{5} \Leftrightarrow AM = \dfrac{{\sqrt {15} }}{3}.\)
Ta có: \(\left\{ \begin{array}{l}\left( P \right) \bot AA'\\\left( {A'B'C'} \right) \bot AM\end{array} \right.\)\( \Rightarrow \widehat {\left( {\left( P \right),\;\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AA',\;AM} \right)} = \widehat {A'MA}\)
\( \Rightarrow \cos \widehat {A'AM} = \dfrac{{AM}}{{AA'}} = \dfrac{{\dfrac{{\sqrt {15} }}{3}}}{{\sqrt {5 + \dfrac{5}{3}} }} = \dfrac{1}{2}.\)
Ta thấy \(\Delta NEF\) là hình chiếu vuông góc của \(\Delta A'B'C'\) lên mặt phẳng \(\left( P \right).\)
\(\begin{array}{l} \Rightarrow {S_{A'B'C'}} = \dfrac{{{S_{NEF}}}}{{\cos \widehat {A'AM}}} = \dfrac{{\dfrac{1}{2}NE.NF}}{{\dfrac{1}{2}}} = 1.2 = 2.\\ \Rightarrow {V_{ABC.A'B'C'}} = {S_{A'B'C'}}.AM = 2.\dfrac{{\sqrt {15} }}{3} = \dfrac{{2\sqrt {15} }}{3}.\end{array}\)
Cho tứ diện đều $ABCD $ có cạnh bằng $3.$ Gọi $M, N$ là hai điểm thay đổi lần lượt thuộc cạnh $BC, BD$ sao cho mặt phẳng $(AMN)$ luôn vuông góc với mặt phẳng $(BCD).$ Gọi $V_1, V_2$ lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện $ABMN.$ Tính $V_1 +V_2$?
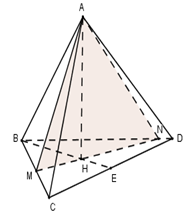
Tứ diện $ABCD$ đều, gọi $H$ là tâm tam giác đều $BCD$ \( \Rightarrow AH \bot \left( {BCD} \right)\)
Có \(\left( {AMN} \right) \bot \left( {BCD} \right) \Rightarrow \left( {AMN} \right) \supset AH \Rightarrow H \in MN\)
\( \Rightarrow {V_{ABMN}} = \dfrac{1}{3}AH.{S_{BMN}}\), với $AH$ không đổi.
Dễ thấy diện tích tam giác $BMN$ nhỏ nhất khi và chỉ khi tam giác $BMN$ đều, khi đó $MN // CD$
\(\dfrac{{BM}}{{BC}} = \dfrac{{BH}}{{BE}} = \dfrac{2}{3} \Rightarrow BM = \dfrac{2}{3}BC = 2 \Rightarrow {S_{BM{N_{\min }}}} = \dfrac{{{2^2}\sqrt 3 }}{4} = \sqrt 3 \)
Diện tích tam giác $BMN $ lớn nhất khi và chỉ khi \(N \equiv D\) hoặc \(M \equiv C\) , khi đó \({S_{BM{N_{\max }}}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}\dfrac{{{3^2}\sqrt 3 }}{4} = \dfrac{{9\sqrt 3 }}{8}\)
Có \(BH = \dfrac{2}{3}BE = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{3^2} - {{\left( {\sqrt 3 } \right)}^2}} = \sqrt 6 \)
\(\begin{array}{l} \Rightarrow {V_1} = \dfrac{1}{3}AH.{S_{BM{N_{{\rm{max}}}}}} = \dfrac{1}{3}\sqrt 6 .\dfrac{{9\sqrt 3 }}{8} = \dfrac{{9\sqrt 2 }}{8}\\\,\,\,\,\,\,{V_2} = \dfrac{1}{3}AH.{S_{BM{N_{{\rm{min}}}}}} = \dfrac{1}{3}\sqrt 6 .\sqrt 3 = \sqrt 2 \\ \Rightarrow {V_1} + {V_2} = \dfrac{{17\sqrt 2 }}{8}\end{array}\)
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là $a,\,\,2a,\,\,3a$ có thể tích lớn nhất bằng
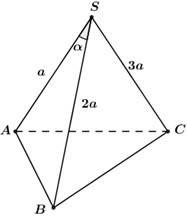
Xét khối chóp tam giác $S.ABC,$ có $\left\{ \begin{array}{l}SA = a,\,\,SB = 2a\\SC = 3a,\,\,\widehat {ASB} = \alpha \end{array} \right.$ và $h$ là khoảng cách từ $C$ đến $(SAB)$
Khi đó, thể tích khối chóp $S.ABC$ là $V = \dfrac{1}{3}.d\left( {C;\left( {SAB} \right)} \right).{S_{\Delta \,SAB}}$ $\left( 1 \right).$
Diện tích tam giác $SAB$ là ${S_{\Delta \,SAB}} = \dfrac{1}{2}.SA.SB.\sin \widehat {ASB} = {a^2}.\sin \alpha $ $\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $V = \dfrac{1}{3}.h.{a^2}.\sin \alpha $ mà $\left\{ \begin{array}{l}\sin \alpha \le 1\\h \le SC = 3a\end{array} \right.$$ \Rightarrow V \le \dfrac{1}{3}.3a.{a^2} = {a^3}.$
Dấu "=" xảy ra khi $\sin \alpha =1$ và $h=SC=3a$ hay hình chóp $S.ABC$ là tứ diện vuông đỉnh $S$.
Cho lăng trụ tam giác đều $ABC.A’B’C’.$ Trên $A’B'$ kéo dài lấy điểm $M$ sao cho \(B'M = \dfrac{1}{2}A'B'\). Gọi $N, P$ lần lượt là trung điểm của $A’C’$ và $B’B.$ Mặt phẳng $(MNP)$ chia khối lăng trụ $ABC.A’B’C’ $ thành hai khối đa diện trong đó khối đa diện chứa đỉnh $A’$ có thể tích \({V_1}\) và khối đa diện chứa đỉnh $C’$ có thể tích \({V_2}\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}\).
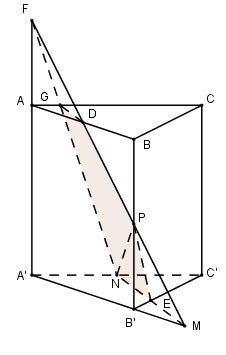
Gọi \(E = MN \cap B'C'\)
Kéo dài $MP$ cắt $AB$ tại $D,$ cắt $AA'$ tại $F.$
Nối $NF,$ cắt $AC$ tại $G.$
Do đó thiết diện của lăng trụ khi cắt bởi mặt phẳng $(MNP)$ là $NEPDG.$
Gọi \({V_1}\) là thể tích khối đa diện chứa đỉnh $A’$ ta có :
\({V_1} = {V_{F.A'MN}} - {V_{F.ADG}} - {V_{P.B'EM}}\)
Ta có:
\({S_{A'MN}} = \dfrac{1}{2}d\left( {N;A'M} \right).A'M = \dfrac{1}{2}.\dfrac{1}{2}d\left( {C';A'B'} \right).\dfrac{3}{2}A'B' = \dfrac{3}{4}{S_{A'B'C'}}\)
\(\Delta BDP = \Delta B'MP \Rightarrow BD = B'M = \dfrac{1}{2}AB \Rightarrow D\) là trung điểm của AB.
\( \Rightarrow \dfrac{{FA}}{{FA'}} = \dfrac{{AD}}{{A'M}} = \dfrac{1}{3} \Rightarrow \dfrac{{FA'}}{{AA'}} = \dfrac{3}{2}\)
\( \Rightarrow \dfrac{{{V_{F.A'MN}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.FA'.{S_{A'MN}}}}{{AA'.{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{3}{2}.\dfrac{3}{4} = \dfrac{3}{8} \Rightarrow {V_{F.A'MN}} = \dfrac{3}{8}{V_{ABC.A'B'C'}} = \dfrac{{3V}}{8}\)
Dễ dàng chứng minh được \(\Delta ADG\) đồng dạng \(\Delta A'MN\) theo tỉ số \(\dfrac{1}{3} \Rightarrow {S_{ADG}} = \dfrac{1}{9}{S_{A'MN}} = \dfrac{1}{{12}}{S_{A'B'C'}}\)
\( \Rightarrow \dfrac{{{V_{F.ADG}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.FA.{S_{ADG}}}}{{AA'.{S_{A'B'C'}}}} = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{{12}} = \dfrac{1}{{72}} \Rightarrow {V_{F.ADG}} = \dfrac{1}{{72}}{V_{ABC.A'B'C'}} = \dfrac{V}{{72}}\)
Áp dụng định lí Menelaus trong tam giác $A’B’C’$ ta có :
\(\dfrac{{MA'}}{{MB'}}.\dfrac{{EB'}}{{EC'}}.\dfrac{{NC'}}{{NA'}} = 1 \Leftrightarrow 3.\dfrac{{EB'}}{{EC'}}.1 = 1 \Leftrightarrow \dfrac{{EB'}}{{EC'}} = \dfrac{1}{3}\)
Áp dụng định lí Menelaus trong tam giác $A’MN$ ta có :
\(\dfrac{{C'N}}{{C'A'}}.\dfrac{{B'A'}}{{B'M}}.\dfrac{{EM}}{{EN}} = 1 \Leftrightarrow \dfrac{1}{2}.2.\dfrac{{EM}}{{EN}} = 1 \Leftrightarrow \dfrac{{EM}}{{EN}} \Rightarrow \dfrac{{ME}}{{MN}} = \dfrac{1}{2}\)
\( \Rightarrow \dfrac{{{S_{B'EM}}}}{{{S_{A'NM}}}} = \dfrac{{MB'}}{{MA'}}.\dfrac{{ME}}{{MN}} = \dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6} \Rightarrow {S_{B'EM}} = \dfrac{1}{6}{S_{A'NM}} = \dfrac{1}{8}{S_{A'B'C'}}\)
\( \Rightarrow \dfrac{{{V_{P.B'EM}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.PB'.{S_{B'EM}}}}{{BB'.{S_{A'B'C'}}}} = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{8} = \dfrac{1}{{48}} \Rightarrow {V_{P.B'EM}} = \dfrac{1}{{48}}V\)
Vậy \({V_1} = \dfrac{{49}}{{144}}V \Rightarrow {V_2} = \dfrac{{95}}{{144}}V \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{49}}{{95}}\)
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(2a,\) gọi \(M\) là trung điểm của $BB'$ và \(P\) thuộc cạnh $DD'$ sao cho $DP\, = \,\dfrac{1}{4}DD'.$ Mặt phẳng $(AMP)$ cắt $CC'$ tại$N.$ Thể tích khối đa diện $AMNPBCD$ bằng
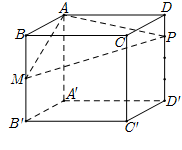
Áp dụng công thức tính nhanh, ta có:
$\dfrac{{{V_{AMNPBCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{BM}}{{BB'}} + \dfrac{{DP}}{{DD'}}} \right) = \dfrac{3}{8} \Rightarrow \,\,{V_{AMNPBCD}} = 3{a^3}.$
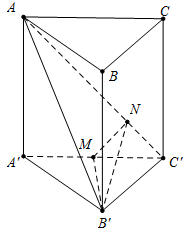
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông, \(AB = BC = a.\) Biết rằng góc giữa hai mặt phẳng \((ACC')\) và \((AB'C')\) bằng \({60^0}\) (tham khảo hình vẽ bên). Thể tích của khối chóp \(B'.ACC'A'\) bằng
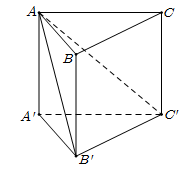
Dựng $B'M \bot A'C' \Rightarrow B'M \bot \left( {ACC'A'} \right)$
Dựng $MN \bot AC' \Rightarrow AC' \bot \left( {MNB'} \right)$
Khi đó $\widehat {\left( {\left( {AB'C'} \right);\left( {AC'A'} \right)} \right)} = \widehat {MNB'} = {60^0}$
Ta có: $B'M = \dfrac{{a\sqrt 2 }}{2} \Rightarrow MN = \dfrac{{B'M}}{{\tan \widehat {MNB'}}} = \dfrac{{a\sqrt 6 }}{6}$
Mặt khác $\tan \widehat {AC'A'} = \dfrac{{MN}}{{C'N}} = \dfrac{{AA'}}{{A'C'}}$
Trong đó $MN = \dfrac{{a\sqrt 6 }}{6};MC' = \dfrac{{a\sqrt 2 }}{2} \Rightarrow C'N = \sqrt {C'{M^2} - M{N^2}} = \dfrac{{a\sqrt 3 }}{3}$
Suy ra $AA' = a$
Thể tích lăng trụ $V = \dfrac{{A{B^2}}}{2}.AA' = \dfrac{{{a^3}}}{2}$$ \Rightarrow {V_{B'.ACC'A'}} = V - {V_{B'.BAC}} = V - \dfrac{V}{3} = \dfrac{2}{3}V = \dfrac{{{a^3}}}{3}.$
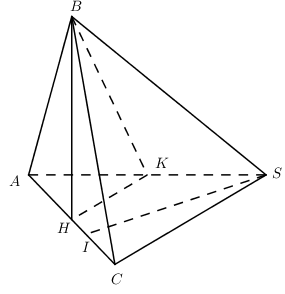
Cho hình chóp \(SABC\) có mặt phẳng \(\left( {SAC} \right)\) vuông góc với mặt phẳng \(\left( {ABC} \right),\;SAB\) là tam giác đều cạnh \(a\sqrt 3 ,\;BC = a\sqrt 3 ,\) đường thẳng \(SC\) tạo với mặt phẳng \(\left( {ABC} \right)\) góc \({60^0}.\) Thể tích của khối chóp \(SABC\) bằng:
Có \(AB = BC = a\sqrt 3 \Rightarrow \Delta ABC\) cân tại $B.$
Gọi $H $ là trung điểm của $AC$ ta có \(BH \bot AC\)
\(\left\{ \begin{array}{l}\left( {ABC} \right) \bot \left( {SAC} \right)\\\left( {ABC} \right) \cap \left( {SAC} \right) = AC\\\left( {ABC} \right) \supset BH \bot AC\end{array} \right. \Rightarrow BH \bot \left( {SAC} \right) \Rightarrow BH \bot SA\,\,\,\left( 1 \right)\)
Gọi $K$ là trung điểm của $SA,$ do tam giác $SAB$ đều \( \Rightarrow BK \bot SA\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow SA \bot \left( {BHK} \right) \Rightarrow SA \bot HK\).
Lại có $HK $ là đường trung bình của tam giác $SAC$ \( \Rightarrow HK//SC \Rightarrow SA \bot SC \Rightarrow \Delta SAC\) vuông tại $S.$
Trong $(SAC)$ kẻ \(SI \bot AC\), tương tự ta có
\(SI \bot \left( {ABC} \right) \Rightarrow \widehat {\left( {SC;\left( {ABC} \right)} \right)} = \widehat {\left( {SC;IC} \right)} = \widehat {SCI} = {60^0}\)
Xét tam giác vuông $SAC$ có \(SC = SA.\cot 60 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a \) \(\Rightarrow AC = \sqrt {{a^2} + 3{a^2}} = 2a\)
\( \Rightarrow {S_{SAC}} = \dfrac{1}{2}SA.SC = \dfrac{1}{2}a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Có $H$ là trung điểm của $AC $ \( \Rightarrow AH = \dfrac{1}{2}AC = a \Rightarrow BH = \sqrt {B{A^2} - A{H^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}BH.{S_{SAC}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 6 }}{6}\)
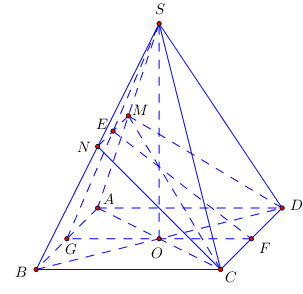
Cho hình chóp đều $S.ABCD $ có đáy là hình vuông cạnh $a,$ $M$ là trung điểm của $SA.$ Biết mặt phẳng $(MCD)$ vuông góc với mặt phẳng $(SAB).$ Thể tích khối chóp $S.ABCD$ là:
Gọi $N$ là trung điểm của $SB$ ta có \(\left( {MCD} \right) \equiv \left( {MNCD} \right)\).
\( \Rightarrow \left( {MNCD} \right) \bot \left( {SAB} \right)\)
Dễ thấy \(\Delta BCN = \Delta ADM\,\,\left( {c.g.c} \right) \Rightarrow CN = DM\)
\( \Rightarrow MNCD\) là hình thang cân. Gọi $E, F$ lần lượt là trung điểm của $MN$ và $CD$ ta có \(EF \bot MN\)
\( \Rightarrow EF \bot \left( {SAB} \right)\)
Gọi $G$ là trung điểm $AB$ ta có $S, E, G$ thẳng hàng.
Đặt \(SA = SB = SC = SD = x\) ta có \(CN = \dfrac{{\sqrt {{x^2} + 2{a^2}} }}{2}\)
Dễ dàng tính được \(EF = \dfrac{{\sqrt {4{x^2} + 7{a^2}} }}{4}\)
Ta có \(EG = \dfrac{1}{2}SG = \dfrac{1}{2}\sqrt {{x^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{\sqrt {4{x^2} - {a^2}} }}{4}\)
\(\Delta EFG\) vuông tại $E$ \( \Rightarrow E{F^2} + E{G^2} = G{F^2} \Leftrightarrow \dfrac{{4{x^2} + 7{a^2}}}{{16}} + \dfrac{{4{x^2} - {a^2}}}{{16}} = {a^2}\)
\( \Leftrightarrow 4{x^2} + 7{a^2} + 4{x^2} - {a^2} = 16{a^2} \Leftrightarrow 8{x^2} = 10{a^2} \Leftrightarrow {x^2} = \dfrac{{5{a^2}}}{4}\)
Xét tam giác vuông $SOB:$ \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {\dfrac{{5{a^2}}}{4} - \dfrac{{{a^2}}}{2}} = \dfrac{{\sqrt 3 a}}{2}\)
Vậy thể tích khối chóp là \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 3 a}}{2}.{a^2} = \dfrac{{\sqrt 3 {a^3}}}{6}\)
