Khối chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $SA = SB = SC = a$, cạnh $SD$ thay đổi. Thể tích khối chóp $S.ABCD$ lớn nhất khi độ dài cạnh $SD$ là:
Trả lời bởi giáo viên
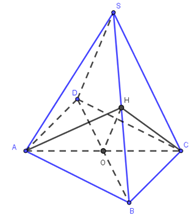
Khối chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $SA = SB = SC = a$
$ \Rightarrow $ Khối chóp $S.ABC$ có: $SA = SB = SC = BA = BC = a$ và có thể tích bằng $\dfrac{1}{2}$ thể tích khối chóp $S.ABCD.$
Như vậy, để thể tích khối chóp $S.ABCD$ lớn nhất thì thể tích khối chóp $S.ABC$ lớn nhất khi $SD $ thay đổi.
Gọi $H$ là trung điểm của $SB.$
$\Delta SAB,\,\,\Delta SBC$ là $2$ tam giác đều, cạnh $a$ $ \Rightarrow AH = CH = \dfrac{{a\sqrt 3 }}{2}$
Và $AH \bot SB,\,\,CH \bot SB \Rightarrow SB \bot (AHC) \Rightarrow BH \bot \left( {AHC} \right)$
\( \Rightarrow {V_{S.ABC}} = 2{V_{B.AHC}}\) \( = 2.\dfrac{1}{3}BH.{S_{AHC}}\) \( = 2.\dfrac{1}{3}.\dfrac{1}{2}SB.{S_{AHC}} = \dfrac{1}{3}a.{S_{AHC}}\)
Mặt khác ${S_{AHC}} = \dfrac{1}{2}.AH.CH.\sin \widehat {AHC} = \dfrac{1}{2}.{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2}\sin \widehat {AHC}$
$ \Rightarrow {V_{S.ABC}}$ lớn nhất khi và chỉ khi $\widehat {AHC} = {90^0} \Leftrightarrow AH \bot HC $ $\Rightarrow \Delta AHC$ vuông cân tại $H$ $ \Rightarrow HO = \dfrac{{AH}}{{\sqrt 2 }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt 2 }} = \dfrac{{a\sqrt 3 }}{{2\sqrt 2 }}$
$OH$ là đường trung bình của $\Delta SBD$ $ \Rightarrow SD = 2.OH = 2.\dfrac{{a\sqrt 3 }}{{2\sqrt 2 }} = \dfrac{{a\sqrt 3 }}{{\sqrt 2 }} = \dfrac{{a\sqrt 6 }}{2}$
Vậy, để thể tích khối chóp $S.ABCD$ lớn nhất khi độ dài cạnh $SD$ là: $\dfrac{{a\sqrt 6 }}{2}$.
Hướng dẫn giải:
- Thể tích $V_{S.ABCD}$ đạt $\max$ nếu $V_{S.ABC}$ đạt $\max $.
- Gọi $H$ là trung điểm của $SB$, tìm $V_{S.ABC}$ và đánh giá tìm $GTLN$ của $V_{S.ABC}$
- Từ đó tính được $SD$

