Câu hỏi:
2 năm trước
Cho tứ diện đều $ABCD $ có cạnh bằng $3.$ Gọi $M, N$ là hai điểm thay đổi lần lượt thuộc cạnh $BC, BD$ sao cho mặt phẳng $(AMN)$ luôn vuông góc với mặt phẳng $(BCD).$ Gọi $V_1, V_2$ lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện $ABMN.$ Tính $V_1 +V_2$?
Trả lời bởi giáo viên
Đáp án đúng: a
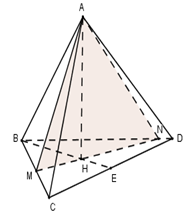
Tứ diện $ABCD$ đều, gọi $H$ là tâm tam giác đều $BCD$ \( \Rightarrow AH \bot \left( {BCD} \right)\)
Có \(\left( {AMN} \right) \bot \left( {BCD} \right) \Rightarrow \left( {AMN} \right) \supset AH \Rightarrow H \in MN\)
\( \Rightarrow {V_{ABMN}} = \dfrac{1}{3}AH.{S_{BMN}}\), với $AH$ không đổi.
Dễ thấy diện tích tam giác $BMN$ nhỏ nhất khi và chỉ khi tam giác $BMN$ đều, khi đó $MN // CD$
\(\dfrac{{BM}}{{BC}} = \dfrac{{BH}}{{BE}} = \dfrac{2}{3} \Rightarrow BM = \dfrac{2}{3}BC = 2 \Rightarrow {S_{BM{N_{\min }}}} = \dfrac{{{2^2}\sqrt 3 }}{4} = \sqrt 3 \)
Diện tích tam giác $BMN $ lớn nhất khi và chỉ khi \(N \equiv D\) hoặc \(M \equiv C\) , khi đó \({S_{BM{N_{\max }}}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}\dfrac{{{3^2}\sqrt 3 }}{4} = \dfrac{{9\sqrt 3 }}{8}\)
Có \(BH = \dfrac{2}{3}BE = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{3^2} - {{\left( {\sqrt 3 } \right)}^2}} = \sqrt 6 \)
\(\begin{array}{l} \Rightarrow {V_1} = \dfrac{1}{3}AH.{S_{BM{N_{{\rm{max}}}}}} = \dfrac{1}{3}\sqrt 6 .\dfrac{{9\sqrt 3 }}{8} = \dfrac{{9\sqrt 2 }}{8}\\\,\,\,\,\,\,{V_2} = \dfrac{1}{3}AH.{S_{BM{N_{{\rm{min}}}}}} = \dfrac{1}{3}\sqrt 6 .\sqrt 3 = \sqrt 2 \\ \Rightarrow {V_1} + {V_2} = \dfrac{{17\sqrt 2 }}{8}\end{array}\)
Hướng dẫn giải:
Công thức tính thể tích khối chóp: \(V = \dfrac{1}{3}h{S_d}.\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
