Khái niệm về khối đa diện

Khối chóp có đáy là đa giác $n$ cạnh thì có $n + 1$ đỉnh (gồm đỉnh $S$ và $n$ đỉnh của đa giác đáy),

$n + 1$ mặt ($1$ mặt đáy và $n$ mặt bên) và $2n$  cạnh ($n$ cạnh bên và $n$ cạnh đáy)

Do đó chỉ có ý A đúng. 

Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt (ví dụ các đỉnh của hình tứ diện)

Không tồn tại 1 đỉnh nào đó của đa diện nào đó là đỉnh chung của ít hơn 3 mặt

Hình tứ diện có \(6\) cạnh và \(4\) mặt nên số cạnh của tứ diện lớn hơn số đỉnh của nó.

Hình tứ diện có \(6\) cạnh và \(4\) đỉnh nên số cạnh của tứ diện lớn hơn số mặt của nó.

Hình đa diện luôn có số đỉnh và số mặt nhỏ hơn số cạnh

Không phải hình đa diện nào cũng có số đỉnh bằng số mặt, ví dụ hình lập phương có 8 đỉnh và 6 mặt

Hình tứ diện có số đỉnh bằng số mặt (bằng 4).

Tứ diện là hình đa diện đơn giản nhất có cạnh bằng \(6\) nên số cạnh của hình đa diện luôn lớn hơn hoặc bằng \(6\).

- Khối lăng trụ tam giác, khối hộp là các khối đa diện.

- Khối tứ diện là một khối đa diện lồi.

- Không phải khi nào lắp ghép 2 khối đa diện ta cũng được khối đa diện lồi.

Các khẳng định A, C, D đúng

Khẳng định B sai vì hai mặt của khối đa diện có thể có điểm chung hoặc không có điểm chung, chẳng hạn hai mặt đối nhau của hình hộp chữ nhật.

Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác. Hình đa diện nhỏ nhất là hình chóp tam giác.

B sai vì hình chóp tam giác có $4$  đỉnh

C sai vì số đỉnh của hình đa diện luôn nhỏ hơn số cạnh

D sai vì số mặt của hình đa diện luôn nhỏ hơn số cạnh

Quan sát bốn hình, có hình C có cạnh là cạnh chung của 4 đa giác, vậy hình này không phải khối đa diện.

Hình đa diện lồi cũng là hình đa diện nên mỗi cạnh của nó là cạnh chung của đúng \(2\) mặt.

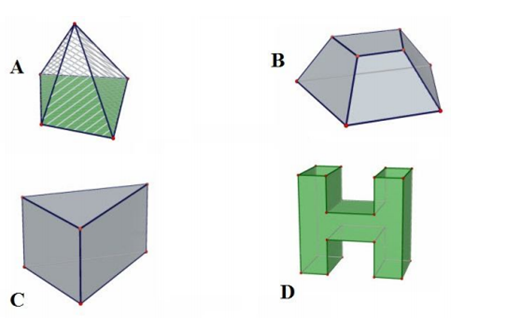
Khối đa diện A là khối chóp tứ giác.

Khối đa diện D không phải là khối đa diện lồi

Khối đa diện B, C là khối đa diện lồi

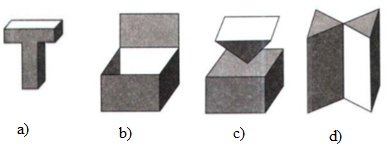
Trong các hình đã cho chỉ có hình a) là khối đa diện.

Hình b) có 3 cạnh ở trên không phải cạnh chung của 2 mặt, hình c) và d) có 1 cạnh là không là cạnh chung của 2 mặt.

Các khối tứ diện, khối hộp, khối lăng trụ tam giác đều là khối đa diện lồi.

Lắp ghép 2 khối hộp chưa chắc được một khối đa diện lồi.      

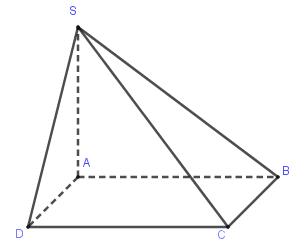
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD,SA \bot AB \Rightarrow \Delta SAB,\Delta SAD\) vuông tại \(A\).

Lại có \(CD \bot SA,CD \bot AD \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại $D.$

\(CB \bot SA,CB \bot AB \Rightarrow CB \bot \left( {SAB} \right) \Rightarrow CB \bot SB \Rightarrow \Delta SCB\) vuông tại \(B\).

Vậy có tất cả $4$ mặt là các tam giác vuông.

Vì mỗi mặt là tam giác nên mỗi mặt có \(3\) cạnh

Do đó M mặt sẽ có \(3M\) cạnh hay đa diện có 3M cạnh.

Tuy nhiên, mỗi cạnh lại là cạnh chung của \(2\) mặt nên mỗi cạnh trên đã được đếm 2 lần.

Số cạnh thực tế của đa diện chỉ là \(C = \frac{{3M}}{2}\) hay \(2C = 3M\).

Vì mỗi đỉnh là đỉnh chung của \(3\) cạnh nên \(D\) đỉnh có \(3D\) cạnh.

Tuy nhiên mỗi cạnh lại là cạnh chung của \(2\) đỉnh nên \(2C = 3D\).

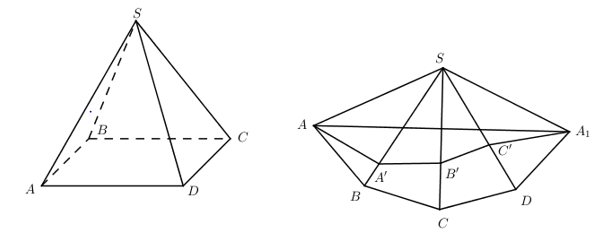
Trải hình chóp S.ABCD trên cùng một mặt phẳng \(\left( {{A_1} \equiv A} \right)\).

Giả sử quãng đường của con kiến đi từ A đến A₁ là AA’B’C’A₁ , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn AA₁.

Xét tam giác SAB có:

\(\begin{array}{l}\cos \angle ASB = \dfrac{{S{A^2} + S{B^2} - A{B^2}}}{{2SA.SB}} = \dfrac{{{6^2} + {6^2} - {4^2}}}{{{{2.6}^2}}} = \dfrac{7}{9}\\ \Rightarrow \angle ASB \approx 38,{9^0}\\ \Rightarrow \angle AS{A_1} = 4\angle ASB \approx 155,{8^0}\end{array}\)

Xét tam giác ASA₁ có :

\(A{A_1}^2 = S{A^2} + SA_1^2 - 2SA.S{A_1}.\cos \angle AS{A_1} \approx 11,73\,\,\left( {cm} \right)\)

Thể tích là \(V = \dfrac{1}{3}Bh = \dfrac{1}{3}.7.6 = 14\)