Cho 2 số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} + 3} \right| + \left| {{z_1} - 3} \right|\)\( = \left| {{z_2} + 4} \right| + \left| {{z_2} - 4} \right| = 10\). Tính giá trị lớn nhất của biểu thức \(\left| {{z_1} - {z_2}} \right|\)
Bước 1: Tìm quỹ tích điểm biểu diễn \({z_1},{z_2}\)
Ta có:
\( + )\left| {{z_1} + 3} \right| + \left| {{z_1} - 3} \right| = 10\)
\( \Rightarrow c = 3,a = 5\)\( \Rightarrow b = \sqrt {{a^2} - {c^2}} = 4\)
\( \Rightarrow \) tập hợp biểu diễn số phức \({z_1}\) là elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\left( {{E_1}} \right)\).
+) \(\left| {{z_2} + 4} \right| + \left| {{z_2} - 4} \right| = 10\)
\( \Rightarrow a = 5,c = 4 \Rightarrow b = 3\)
\( \Rightarrow \) Tập hợp biểu diễn số phức \({z_2}\) là Elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\left( {{E_1}} \right)\).
Bước 2: Gọi \(M\) là điểm biểu diễn \({z_1},N\) là điểm biểu diễn số phức \({z_2}\). Gọi \(P = MN \cap \left( {{E_1}} \right)\). Tìm \(\max \left| {{z_1} - {z_2}} \right|\)
Đồ thị của \(\left( {{E_1}} \right)\) và \(\left( {{E_2}} \right)\):
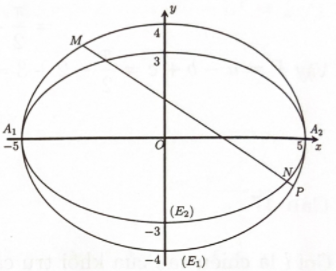
Gọi \(M\) là điểm biểu diễn \({z_1},N\) là điểm biểu diễn số phức \({z_2}\).
Khi đó \(\left| {{z_1} - {z_2}} \right| = MN\).
Gọi \(P = MN \cap \left( {{E_1}} \right)\)
\( \Rightarrow MN \le MP \le {A_1}{A_2} = 10\) (không đổi).
\( \Rightarrow \max \left| {{z_1} - {z_2}} \right| = \max MN = 10\).
Cho số phức \(z\) thỏa mãn \(2\left| z \right| = \left| {{z^2} + 4} \right|\). Tìm giá trị lớn nhất của \(\left| z \right|\).
Ta có: \(\left| {{z^2} + 4} \right| \ge \left| {{z^2}} \right| - \left| 4 \right| = {\left| z \right|^2} - 4 \Rightarrow 2\left| z \right| \ge {\left| z \right|^2} - 4 \Leftrightarrow {\left| z \right|^2} - 2\left| z \right| - 4 \le 0 \Leftrightarrow 1 - \sqrt 5 \le \left| z \right| \le 1 + \sqrt 5 \)
\( \Rightarrow {\left| z \right|_{\max }} = 1 + \sqrt 5 \) .
Biết số phức thỏa mãn \(\left| {iz - 3} \right| = \left| {z - 2 - i} \right|\)và \(\left| z \right|\) có giá trị nhỏ nhất. Phần thực của số phức z bằng
Đặt \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\)
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {iz - 3} \right| = \left| {z - 2 - i} \right|\\ \Leftrightarrow \left| {i\left( {a + bi} \right) - 3} \right| = \left| {a + bi - 2 - i} \right|\\ \Leftrightarrow \left| {\left( { - 3 - b} \right) + ai} \right| = \left| {\left( {a - 2} \right) + \left( {b - 1} \right)i} \right|\\ \Leftrightarrow {\left( {b + 3} \right)^2} + {a^2} = {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {b^2} + 6b + 9 + {a^2} = {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 4a + 8b + 4 = 0\\ \Leftrightarrow a + 2b + 1 = 0\\ \Leftrightarrow a = - 2b - 1\end{array}\)
Ta có:
\(\begin{array}{l}\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt {{{\left( {2b + 1} \right)}^2} + {b^2}} \\\,\,\,\,\,\, = \sqrt {5{b^2} + 4b + 1} = \sqrt {5\left( {{b^2} + \dfrac{4}{5}b} \right) + 1} \\\,\,\,\,\,\, = \sqrt {5\left( {{b^2} + 2.b.\dfrac{2}{5} + \dfrac{4}{{25}}} \right) - \dfrac{4}{5} + 1} \\\,\,\,\,\,\, = \sqrt {5{{\left( {b + \dfrac{2}{5}} \right)}^2} + \dfrac{1}{5}} \ge \dfrac{{\sqrt 5 }}{5}\end{array}\)
Dấu bằng xảy ra khi và chỉ khi \(b = - \dfrac{2}{5} \Rightarrow a = - \dfrac{1}{5}.\)
Vậy \({\mathop{\rm Re}\nolimits} z = a = - \dfrac{1}{5}\).
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| z \right| = 1\) và \(\left| w \right| = 2\). Khi \(\left| {z + i\overline w - 6 + 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - w} \right|\) bằng:
Dùng phương pháp hình học \( \to \) Kỹ năng dồn số phức.
* \(P = \left| {z + i\,\overline w - 6 + 8i} \right| = \left| {\left( {z - 6 + 8i} \right) - \left( { - i\overline w } \right)} \right| = \left| {u - v} \right|\).
Trong đó: \(\left\{ \begin{array}{l}u = z - 6 + 8i\\v = - i\overline w \end{array} \right.\), \(u\) có điểm biểu diễn là \(A\), \(v\) có điểm biểu diễn là \(B\).
\( \Rightarrow P = \left| {u - v} \right| = AB \Rightarrow \) Cần đạt Min.
* \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z - 6 + 8i} \right) + 6 - 8i} \right| = 1 \Leftrightarrow \left| {u + 6 - 8i} \right| = 1\).
\( \Rightarrow \) Tập hợp điểm \(A\) biểu diễn số phức \(u\) là đường tròn: \(\left( {{C_1}} \right)\): \(\left\{ \begin{array}{l}I\left( { - 6;8} \right)\\{R_1} = 1\end{array} \right.\).
* \(\left| w \right| = 2 \Leftrightarrow \left| {\overline w } \right| = 2 \Leftrightarrow \left| { - i} \right|.\left| {\overline w } \right| = \left| { - i} \right|.2\) \( \Rightarrow \left| { - i\overline w } \right| = 2 \Leftrightarrow \left| v \right| = 2\).
\( \Rightarrow \) Tập hợp điểm \(B\) biểu diễn số phức \(v\) là đường tròn \(\left( {{C_2}} \right):\,\,\left\{ \begin{array}{l}O\left( {0;0} \right)\\{R_2} = 2\end{array} \right.\).
Có \(\left\{ \begin{array}{l}IA = {R_1} = 1\\OB = {R_2} = 2\\OI = 10\end{array} \right.\)
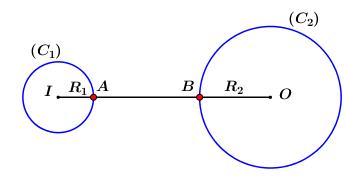
\( \Rightarrow A{B_{\min }} = IO - {R_1} - {R_2} = 10 - 1 - 2 = 7\).
Min đạt được khi: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \dfrac{9}{{10}}\overrightarrow {OI} \Rightarrow A\left( {\dfrac{{ - 27}}{5};\dfrac{{36}}{5}} \right) \Rightarrow u = - \dfrac{{27}}{5} + \dfrac{{36}}{5}i\\\overrightarrow {OB} = \dfrac{1}{5}\overrightarrow {OI} \Rightarrow B\left( {\dfrac{{ - 6}}{5};\dfrac{8}{5}} \right) \Rightarrow v = - \dfrac{6}{5} + \dfrac{8}{5}i\end{array} \right.\).
\( \Rightarrow \left\{ \begin{array}{l}z = u + 6 - 8i = \dfrac{3}{5} - \dfrac{4}{5}i\\ - i\overline w = v \Rightarrow \overline w = \dfrac{v}{{ - i}} = \dfrac{{ - \dfrac{6}{5} + \dfrac{8}{5}i}}{{ - i}} = - \dfrac{8}{5} - \dfrac{6}{5}i \Rightarrow w = - \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
\( \Rightarrow \left| {z - w} \right| = \left| {\left( {\dfrac{3}{5} - \dfrac{4}{5}i} \right) - \left( { - \dfrac{8}{5} + \dfrac{6}{5}i} \right)} \right| = \dfrac{{\sqrt {221} }}{5}\).
Cho số phức \(z\) thỏa mãn \(|z - 3 - 4i| = 1\). Môđun lớn nhất của số phức \(z\) là:
Theo bất đẳng thức chứa dấu giá trị tuyệt đối ta có
\(1 = |z - 3 - 4i| \ge |z| - |3 + 4i| = |z| - 5 \Rightarrow |z| \le 6\)
Cho số phức \(z\) thỏa mãn \(|z - 2 - 3i| = 1\). Tìm giá trị lớn nhất của \(|z|\).
Theo bất đẳng thức chứa dấu giá trị tuyệt đối ta có
\(|z| = |(z - 2 - 3i) + (2 + 3i)| \le |z - 2 - 3i| + |2 + 3i| = 1 + \sqrt {13} \)
- Xét các số phức \(z\) thỏa mãn \(|z - 1 + 2i| = \sqrt 5 \). Tìm số phức \(w\) có mô đun lớn nhất, biết rằng \(w = z + 1 + i\).
- Mô đun của một số phức là khoảng cách từ điểm O đến điểm biểu diễn số phức đó.
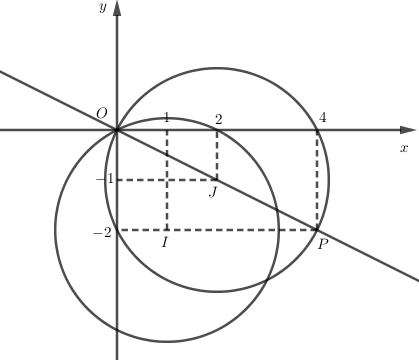
Các điểm $M\left( {x;y} \right)$ biểu diễn số phức \(z\) thỏa mãn \(|z - (1 - 2i)| = \sqrt 5 \) thuộc đường tròn tâm $I(1;-2)$ (biểu diễn số phức \(z_2=1-2i\)) bán kính bằng \(\sqrt 5 \).
Ta có \(w = z + 1 + i\) nên \(z=w-1-i\). Thay vào \(|z - 1 + 2i| = \sqrt 5 \) ta được:
\(|(w-1-i )- 1 + 2i| = \sqrt 5 \) hay \(|w-(2-i)|=\sqrt 5\)
Từ đó các điểm biểu diễn $w$ thuộc đường tròn tâm J(2;-1) (điểm biểu diễn số phức 2-i) bán kính \(\sqrt 5 \)
Thay tọa độ điểm O vào \(|w-(2-i)|=\sqrt 5\) ta thấy \(\left| {2 - i} \right| = \sqrt 5 \) nên đường tròn này đi qua gốc $O$.
Quan sát hình vẽ trên ta thấy để w có mô đun lớn nhất thì khoảng cách từ O đến điểm trên đường tròn tâm J bán kính \(\sqrt 5 \) lớn nhất hay $OP$ là đường kính của đường tròn đó, tức P đối xứng với O qua J, vậy $w = 2\left( {2 - i} \right) = 4 - 2i$
Trong các số phức $z$ thỏa mãn \(|z - 2 - 4i| = |z - 2i|\). Tìm số phức \(z\) có mô đun nhỏ nhất.
Giả sử \(z = a + bi\), ta có
\(|a + bi - 2 - 4i| = |a + bi - 2i| \Leftrightarrow {(a - 2)^2} + {(b - 4)^2} = {a^2} + {(b - 2)^2}\)
\( \Leftrightarrow - 4a + 4 - 8b + 16 = - 4b + 4 \Leftrightarrow - 4a - 4b + 16 = 0 \Leftrightarrow a + b = 4 \Rightarrow b = 4 - a\)
Ta có
\(|z| = \sqrt {{a^2} + {b^2}} = \sqrt {{a^2} + {{(4 - a)}^2}} = \sqrt {2{a^2} - 8a + 16} = \sqrt {2({a^2} - 4a + 4) + 8} = \sqrt {2{{(a - 2)}^2} + 8} \ge 2\sqrt 2 \)
\( \Rightarrow \min \left| z \right| = 2\sqrt 2 \Rightarrow a = 2,b = 2 \Rightarrow z = 2 + 2i\).
Cho số phức \(z\) thỏa mãn \(\left| {\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1} \right| = 2\). Giá trị lớn nhất của mođun phức \(z\) là
Bước 1: Đặt \(z = x + yi(x,y \in \mathbb{R})\). Tìm tập hợp điểm biểu diễn z.
Đặt \(z = x + yi(x,y \in \mathbb{R})\).
Ta có \(\left| {\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1} \right| = 2 \Leftrightarrow | - iz + 1| = 2 \Leftrightarrow |z + i| = 2\) \( \Leftrightarrow {x^2} + {(y + 1)^2} = 4\).
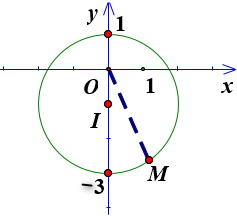
Vậy tập hợp điểm \(M\) biểu diễn số phức \(z\) nằm trên đường tròn tâm \(I(0; - 1)\) và bán kính \(R = 2\).
Bước 2: Tìm max|z|.
Ta có \(|z| = OM\).
Do đó, |z| lớn nhất khi OM lớn nhất.
Dựa vào hình vẽ ta thấy OM lớn nhất khi và chỉ khi O, M, I thẳng hàng \( \Rightarrow \max |z| = 3\).
Biết số phức $z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)$ thỏa mãn điều kiện $\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right|$ đồng thời có môđun nhỏ nhất. Tính giá trị biểu thức \(M = {x^2} + {y^2}.\)
Ta có $\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right| \Rightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 4} \right)}^2}} = \sqrt {{x^2} + {{\left( {y - 2} \right)}^2}} $
$ \Leftrightarrow {x^2} + {y^2} - 4x - 8y + 20 = {x^2} + {y^2} - 4y + 4 \Rightarrow y = 4 - x.$
Khi đó $\left| z \right| = \sqrt {{x^2} + {y^2}} = \sqrt {{x^2} + {{\left( {4 - x} \right)}^2}} = \sqrt {2{x^2} - 8x + 16} = \sqrt {2{{\left( {x - 2} \right)}^2} + 8} \ge 2\sqrt 2 .$
Vậy môđun nhỏ nhất của $z$ là $2\sqrt 2 .$ Xảy ra $ \Leftrightarrow \,\,x = y = 2 \Rightarrow M = 8.$
Cho các số phức \(z,{\rm{ }}w\) thỏa mãn \(\left| {z + 2 - 2i} \right| = \left| {z - 4i} \right|\) và $w = iz + 1$. Giá trị nhỏ nhất của biểu thức \(P = \left| w \right|\) là:
Đặt $z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)$.
Ta có \(\left| {z + 2 - 2i} \right| = \left| {z - 4i} \right| \Rightarrow \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 2} \right)}^2}} = \sqrt {{x^2} + {{\left( {y - 4} \right)}^2}} \)
\( \Leftrightarrow {\left( {x + 2} \right)^2} + {\left( {y - 2} \right)^2} = {x^2} + {\left( {y - 4} \right)^2} \Rightarrow y = 2 - x.\)
Khi đó $w = iz + 1 = i\left( {x + yi} \right) + 1 = ix - y + 1 = ix - \left( {2 - x} \right) + 1 = \left( {x - 1} \right) + xi.$
Suy ra $\left| w \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {x^2}} = \sqrt {2{{\left( {x - \dfrac{1}{2}} \right)}^2} + \dfrac{1}{2}} \ge \dfrac{{\sqrt 2 }}{2}$.
Dấu “=” xảy ra khi \(x = \dfrac{1}{2} \Rightarrow y = \dfrac{3}{2} \Rightarrow z = \dfrac{1}{2} + \dfrac{3}{2}i\).
Cho số phức \(z\) thỏa mãn \(\left| {{z^2} - 2z + 5} \right| = \left| {\left( {z - 1 + 2i} \right)\left( {z + 3i - 1} \right)} \right|\). Tìm giá trị nhỏ nhất của \(P = \left| w \right|\), với \(w = z - 2 + 2i\).
Ta có $\left| {{z^2} - 2z + 5} \right| = \left| {\left( {z - 1 + 2i} \right)\left( {z + 3i - 1} \right)} \right|$
$ \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} + 4} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} - {{\left( {2i} \right)}^2}} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right|$
\( \Leftrightarrow \left| {\left( {z - 1 + 2i} \right)\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow \left[ \begin{array}{l}z - 1 + 2i = 0{\rm{ }}(1)\\\left| {\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z + 3i - 1} \right)} \right|{\rm{ }}(2)\end{array} \right..\)
Từ $\left( 1 \right) \Rightarrow z = 1 - 2i \Rightarrow w = - 1 \Rightarrow P = \left| w \right| = 1.$
Xét $\left( 2 \right)$. Gọi \(z = x + yi{\rm{ }}\left( {x;y \in \mathbb{R}} \right)\).
Ta có $\left| {\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z + 3i - 1} \right)} \right| $ $ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} $ $\Leftrightarrow y = - \dfrac{1}{2}.$
Khi đó $w = x - \dfrac{1}{2}i - 2 + 2i = \left( {x - 2} \right) + \dfrac{3}{2}i$ $ \Rightarrow P = \left| w \right| = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2}} \ge \dfrac{3}{2}$
Vậy \({P_{\min }} =1.\)
Cho số phức \(z\) thỏa mãn \(\left| {z + 1 - i} \right| = \left| {z - 3i} \right|\). Tính môđun lớn nhất \({\left| w \right|_{\max }}\) của số phức \(w = \dfrac{1}{z}.\)
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\).
Ta có \(\left| {z + 1 - i} \right| = \left| {z - 3i} \right|\), suy ra \(\sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 1} \right)}^2}} = \sqrt {{x^2} + {{\left( {y - 3} \right)}^2}} \Leftrightarrow 2x + 4y - 7 = 0\)
Suy ra tập hợp điểm biểu diễn các số phức \(z\) là đường thẳng \(\Delta :2x + 4y - 7 = 0.\)
Ta có \({\left| z \right|_{\min }} = d\left( {O;\Delta } \right) = \dfrac{{\left| { - 7} \right|}}{{\sqrt {{2^2} + {4^2}} }} = \dfrac{{7\sqrt 5 }}{{10}} \Rightarrow {\left| w \right|_{\max }} = \dfrac{1}{{{{\left| z \right|}_{\min }}}} = \dfrac{{2\sqrt 5 }}{7}.\)
Cho hai số phức ${z_1},{\rm{ }}\,{z_2}$ thỏa mãn \(\left| {{z_1} - 2i} \right| = 3\) và \(\left| {{z_2} + 2 + 2i} \right| = \left| {{z_2} + 2 + 4i} \right|\). Giá trị nhỏ nhất của biểu thức \(P = \left| {{z_1} - {z_2}} \right|\) bằng:
Đặt ${z_1} = {x_1} + {y_1}i$ và ${z_2} = {x_2} + {y_2}i$ với ${x_1},{\rm{ }}{x_2},{\rm{ }}{y_1},{\rm{ }}{y_2} \in \mathbb{R}.$
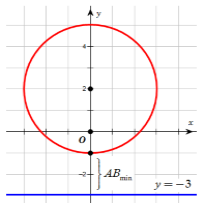
\(\left| {{z_1} - 2i} \right| = 3 \to {x_1}^2 + {\left( {{y_1} - 2} \right)^2} = 9\) suy ra tập hợp các số phức \({z_1}\) là đường tròn \(\left( C \right):{x^2} + {\left( {y - 2} \right)^2} = 9\).
\(\left| {{z_2} + 2 + 2i} \right| = \left| {{z_2} + 2 + 4i} \right|\)
\( \to {\left( {{x_2} + 2} \right)^2} + {\left( {{y_2} + 2} \right)^2} = {\left( {{x_2} + 2} \right)^2} + {\left( {{y_2} + 4} \right)^2}\)
\( \Leftrightarrow {y_2} + 3 = 0\) suy ra tập hợp các số phức \({z_2}\) là đường thẳng \(d:y = - 3\).
Ta có \(P = \left| {{z_1} - {z_2}} \right| = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \). Đây chính là khoảng cách từ điểm $B\left( {{x_2};{y_2}} \right) \in d$ đến điểm $A\left( {{x_1};{y_1}} \right) \in \left( C \right)$.
Do đó ${\left| {{z_2} - {z_1}} \right|_{\min }} \Leftrightarrow A{B_{\min }}.$
Dựa vào hình vẽ ta tìm được $A{B_{\min }} = 2$ khi \(A\left( {0; - 1} \right),{\rm{ }}B\left( {0; - 3} \right)\).
Cho số phức \({z_1}\) thỏa mãn \({\left| {{z_1} - 2} \right|^2} - {\left| {{z_1} + i} \right|^2} = 1\) và số phức \({z_2}\) thỏa mãn \(\left| {{z_2} - 4 - i} \right| = \sqrt 5 \). Tìm giá trị nhỏ nhất của \(P = \left| {{z_1} - {z_2}} \right|\).
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\). Ta có
${{\left| z-2 \right|}^{2}}-{{\left| z+i \right|}^{2}}=1$ $\to {{\left( x-2 \right)}^{2}}+{{y}^{2}}-{{x}^{2}}-{{\left( y+1 \right)}^{2}}=1$ $\xrightarrow{{}}2x+y-1=0$.
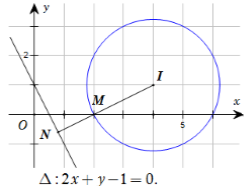
Suy ra tập hợp các số phức \({z_1}\) là đường thẳng $\Delta :2x + y - 1 = 0.$
$\left| z-4-i \right|=\sqrt{5}\xrightarrow{{}}\left| \left( x-4 \right)+\left( y-1 \right)i \right|=\sqrt{5}$
$\Leftrightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=5$
Suy ra tập hợp các số phức \({z_2}\) là đường tròn $\left( C \right):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 5$ có tâm \(I\left( {4;1} \right)\) và bán kính \(R = \sqrt 5 .\)
Khi đó biểu thức \(P = \left| {{z_1} - {z_2}} \right|\) là khoảng cách từ một điểm thuộc \(\Delta \) đến một điểm thuộc \(\left( C \right)\).
Từ đó suy ra \({P_{\min }} = MN = \left| {d\left[ {I,\Delta } \right] - R} \right| \) \(= \left| {\dfrac{8}{{\sqrt 5 }} - \sqrt 5 } \right| = \dfrac{{3\sqrt 5 }}{5}.\)
Biết số phức $z = x + yi{\rm{ }}\left( {x;y \in \mathbb{R}} \right)$ thỏa mãn đồng thời các điều kiện $\left| {z - \left( {3 + 4i} \right)} \right| = \sqrt 5 $ và biểu thức $P = {\left| {z + 2} \right|^2} - {\left| {z - i} \right|^2}$ đạt giá trị lớn nhất. Tính $\left| z \right|$.
Vì $\left| {z - \left( {3 + 4i} \right)} \right| = \sqrt 5 \Rightarrow {\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 5.$
Suy ra tập hợp các điểm biểu diễn số phức \(z\) là đường tròn $\left( C \right)$ có tâm $I\left( {3;4} \right)$ và bán kính $R = \sqrt 5 $.
Ta có $P = {\left| {\left( {x + 2} \right) + yi} \right|^2} - {\left| {x + \left( {y - 1} \right)i} \right|^2} = {\left( {x + 2} \right)^2} + {y^2} - \left[ {{x^2} + {{\left( {y - 1} \right)}^2}} \right]$.
$ = 4x + 2y + 3 \Leftrightarrow 4x + 2y + 3 - P = 0.$
Ta tìm $P$ sao cho đường thẳng $\Delta :4x + 2y + 3 - P = 0$ và đường tròn $\left( C \right)$ có điểm chung $ \Leftrightarrow d\left[ {I,\Delta } \right] \le R \Leftrightarrow \dfrac{{\left| {12 + 8 + 3 - P} \right|}}{{\sqrt {20} }} \le \sqrt 5 \Leftrightarrow \left| {23 - P} \right| \le 10 \Leftrightarrow 13 \le P \le 33.$
Do đó ${P_{\max }} = 33$. Dấu $'' = ''$ xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}4x + 2y - 30 = 0\\{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = \,5\end{array} \right.$.
Vậy $\left| z \right| = \sqrt {{5^2} + {{\left( { - 5} \right)}^2}} = 5\sqrt 2 $.
Trong mặt phẳng phức Oxy, các số phức \(z\) thỏa mãn \(|z + 2i - 1| = |z + i|\). Tìm số phức \(z\) được biểu diễn bởi điểm \(M\) sao cho MA ngắn nhất với \(A(1,3)\).
Bước 1: Gọi \(M(x,y)\) là điểm biểu diễn số phức \(z = x + yi(x,y \in \mathbb{R})\). Các điểm biểu diễn số phức \(1 - 2i\) và \( - i\).
Gọi \(M(x,y)\) là điểm biểu diễn số phức \(z = x + yi(x,y \in \mathbb{R})\).
Gọi \(E(1, - 2)\) là điểm biểu diễn số phức \(1 - 2i\).
Gọi \(F(0, - 1)\) là điểm biểu diễn số phức \( - i\).
\(\overrightarrow {EF} = \left( { - 1;1} \right)\)
Đường thẳng EF qua E và nhận \(\overrightarrow n \left( {1;1} \right)\) làm vectơ pháp tuyến có phương trình là
\(EF:x - y - 2 = 0\)
Bước 2: Tìm tập hợp điểm biểu diễn số phức z và tìm z để MA ngắn nhất
Ta có \(|z + 2i - 1| = |z + i| \Leftrightarrow ME = MF \Rightarrow \) Tập hợp điểm biểu diễn số phức \(z\) là đường trung trực của \(EF:x - y - 2 = 0\).
Để MA ngắn nhất thì \(MA \bot EF\) tại \(M \Leftrightarrow M(3,1) \Rightarrow z = 3 + i\).
Đề thi THPT QG – 2021 lần 1– mã 104
Xét các số phức \(z,{\rm{w}}\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {\rm{w}} \right| = 2.\) Khi \(\left| {z + i\overline {\rm{w}} + 6 + 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng
Gọi \(M\) và \(N\) lần lượt là các điểm biểu diễn số phức \(z + 6 + 8i\) và \(i\overline {\rm{w}} \).
Ta có: \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z + 6 + 8i} \right) + \left( { - 6 - 8i} \right)} \right| = 1 \Leftrightarrow MI = 1\) với \(I\left( { - 6; - 8} \right).\)
Suy ra tập hợp điểm \(M\) là đường tròn \(\left( {{T_1}} \right)\) tâm \(I\left( {6;8} \right)\) và bán kính \({R_1} = 1\).
Ta có: \(\left| {i\overline {\rm{w}} } \right| = \left| i \right|.\left| {\overline {\rm{w}} } \right| = 2.\)
Suy ra tập hợp điểm \(N\) là đường tròn \(\left( {{T_2}} \right)\) tâm \(O\) và bán kính \({R_2} = 2\).
Ta có: \(P = \left| {z + \overline {iw} + 6 + 8i} \right| = MN\)
\( \Rightarrow \min P = OI - {R_1} - {R_2} = 10 - 1 - 2 = 7\) (do \(\left( {{T_1}} \right)\) và \(\left( {{T_2}} \right)\) rời nhau).
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {OM} = \dfrac{9}{{10}}\overrightarrow {OI} \\\overrightarrow {ON} = \dfrac{1}{5}\overrightarrow {OI} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}M\left( { - \dfrac{{27}}{5}; - \dfrac{{36}}{5}} \right)\\N\left( { - \dfrac{6}{5}; - \dfrac{8}{5}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = \dfrac{3}{5} + \dfrac{4}{5}i\\{\rm{w}} = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
Vậy \(\left| {z - {\rm{w}}} \right| = \left| {\dfrac{3}{5} + \dfrac{4}{5}i - \dfrac{8}{5} - \dfrac{6}{5}i} \right| = \dfrac{{\sqrt {29} }}{5}\)
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| {w - i} \right| = 2,\,\,z + 2 = iw\). Gọi \({z_1},\,\,{z_2}\) lần lượt là các số phức mà tại đó \(\left| z \right|\) đạt giá trị nhỏ nhất và giá trị lớn nhất. Môđun \(\left| {{z_1} + {z_2}} \right|\) bằng:
Theo bài ra ta có:
\(\begin{array}{l}z + 2 = iw \Rightarrow w = \dfrac{{z + 2}}{i}\\\left| {w - i} \right| = 2 \Rightarrow \left| {\dfrac{{z + 2}}{i} - i} \right| = 2 \Leftrightarrow \left| {z + 2 + 1} \right| = 2 \Leftrightarrow \left| {z + 3} \right| = 2\end{array}\)
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(I\left( { - 3;0} \right)\) bán kính \(R = 2\).
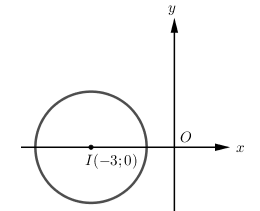
Gọi \(M\) là điểm biểu diễn số phức \(z\), dựa vào hình vẽ ta có:
\(\left\{ \begin{array}{l}{\left| z \right|_{\min }} \Leftrightarrow O{M_{\min }} \Leftrightarrow M\left( { - 1;0} \right) \Rightarrow {z_1} = - 1\\{\left| z \right|_{\max }} \Leftrightarrow O{M_{\max }} \Leftrightarrow M\left( { - 5;0} \right) \Rightarrow {z_2} = - 5\end{array} \right. \Rightarrow \left| {{z_1} + {z_2}} \right| = 6\).
Với hai số phức \({z_1}\) và \({z_2}\) thỏa mãn \({z_1} + {z_2} = 8 + 6i\) và \(\left| {{z_1} - {z_2}} \right| = 2\), tìm giá trị lớn nhất của \(P = \left| {{z_1}} \right| + \left| {{z_2}} \right|\).
Bước 1: Tính \(2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)\)
Ta có \(\left| {{z_1} + {z_2}} \right| = |8 + 6i| = 10\).
Suy ra \(2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right) = {\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2}\)\( = 100 + 4 = 104\).
Bước 2: Tìm P max
Ta có \(P = \left| {{z_1}} \right| + \left| {{z_2}} \right| \le \sqrt {2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)} = \sqrt {104} = 2\sqrt {26} \).
Đẳng thức xảy ra khi và chỉ khi \(\left\{ {\begin{array}{*{20}{l}}{\left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt {26} }\\{{z_1} + {z_2} = 8 + 6i}\\{\left| {{z_1} - {z_2}} \right| = 2}\end{array}} \right.\)
Vậy \(\max P = 2\sqrt {26} \).

