Cho số phức \(z\) thỏa mãn \(\left| {\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1} \right| = 2\). Giá trị lớn nhất của mođun phức \(z\) là
Trả lời bởi giáo viên
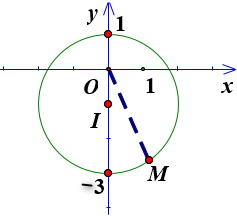
Bước 1: Đặt \(z = x + yi(x,y \in \mathbb{R})\). Tìm tập hợp điểm biểu diễn z.
Đặt \(z = x + yi(x,y \in \mathbb{R})\).
Ta có \(\left| {\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1} \right| = 2 \Leftrightarrow | - iz + 1| = 2 \Leftrightarrow |z + i| = 2\) \( \Leftrightarrow {x^2} + {(y + 1)^2} = 4\).
Vậy tập hợp điểm \(M\) biểu diễn số phức \(z\) nằm trên đường tròn tâm \(I(0; - 1)\) và bán kính \(R = 2\).
Bước 2: Tìm max|z|.
Ta có \(|z| = OM\).
Do đó, |z| lớn nhất khi OM lớn nhất.
Dựa vào hình vẽ ta thấy OM lớn nhất khi và chỉ khi O, M, I thẳng hàng \( \Rightarrow \max |z| = 3\).
Hướng dẫn giải:
Bước 1: Đặt \(z = x + yi(x,y \in \mathbb{R})\). Tìm tập hợp điểm biểu diễn z.
Bước 2: Tìm max|z|.

