Số phức và các phép toán cộng, trừ, nhân, chia số phức

Phần thực của số phức \(z\) là \(a\).

Số phức \(z = \sqrt 2 i - 1 =  - 1 + \sqrt 2 i\) có phần thực là \( - 1\).

Hai số phức \(z = a + bi,z' = a + b'i\) bằng nhau nếu \(b = b'\)

Số phức liên hợp của số phức \(z = a - bi\) là \(\overline z  = a + bi\).

Ta có:

\(\begin{array}{l}\,\,\,\,\left( {a + bi} \right) - 2\left( {a - bi} \right) =  - 1 + 6i\\ \Leftrightarrow  - a + 3bi =  - 1 + 6i\\ \Leftrightarrow \left\{ \begin{array}{l} - a =  - 1\\3b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\end{array}\)

Vậy \(a + b = 1 + 2 = 3\).

Ta có:

\(\begin{array}{l}w = 2z + \left( {1 + i} \right)\bar z\\w = 2\left( {2 - 3i} \right) + \left( {1 + i} \right)\left( {2 + 3i} \right)\\w = 4 - 6i + 2 + 3i + 2i - 3\\w = 3 - i\\ \Rightarrow \left| w \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}}  = \sqrt {10} .\end{array}\)

Áp dụng công thức tổng của cấp số nhân với số hạng đầu \({u_1} = 1 + i\) và công bội \(q = 1 + i\) ta có:

\(\overline z  = 2 + i + {(1 + i)^2} + {(1 + i)^3}\)\( +  \ldots  + {(1 + i)^{2019}}\)\( = 1 + \left( {1 + i} \right) + {(1 + i)^2} + {(1 + i)^3}\)\( +  \ldots  + {(1 + i)^{2019}}\)

\( = \dfrac{{1 - {{(1 + i)}^{2020}}}}{{1 - (1 + i)}} = \dfrac{{1 - {{\left( {1 + i} \right)}^{2020}}}}{{ - i}}\)\( = \dfrac{{i\left[ {1 - {{\left( {1 + i} \right)}^{2020}}} \right]}}{{ - {i^2}}} = i\left[ {1 - {{\left( {1 + i} \right)}^{2020}}} \right]\)\(\begin{array}{l} = i - i{\left[ {{{\left( {1 + i} \right)}^2}} \right]^{1010}} = i - i{\left( {2i} \right)^{1010}}\\ = i - {2^{1010}}.{i^{1011}} = i - {2^{1010}}.{i^3}.{i^{1008}}\\ = i + {2^{1010}}i = i\left( {1 + {2^{1010}}} \right)\end{array}\)

\( \Rightarrow z =  - i\left( {1 + {2^{1010}}} \right)\)

Phần ảo của số phức \(z\) là \( - \left( {{2^{1010}} + 1} \right)\)

\(\begin{array}{l}z = \left( {2 - 3i} \right){\left( {1 + i} \right)^4}\\z = \left( {2 - 3i} \right){\left[ {{{\left( {1 + i} \right)}^2}} \right]^2}\\z = \left( {2 - 3i} \right){\left( {1 + 2i + {i^2}} \right)^2}\\z = \left( {2 - 3i} \right).{\left( {2i} \right)^2}\\z = \left( {2 - 3i} \right).\left( { - 4} \right)\\z =  - 8 + 12i\end{array}\)

Vậy \(\left| z \right| = \sqrt {{{\left( { - 8} \right)}^2} + {{12}^2}}  = \sqrt {208}  = 4\sqrt {13} \).

\(|z| = \sqrt {{3^2} + {{( - 1)}^2}}  = \sqrt {10} \)

Ta có \(z = \left( {3 - 2i} \right){\left( {1 + i} \right)^2} = 4 + 6i\)

Khi đó ta có:

\(\begin{array}{l}w = iz + \overline z  = i\left( {4 + 6i} \right) + \left( {4 - 6i} \right) =  - 2 - 2i\\ \Rightarrow \left| w \right| = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2 .\end{array}\)

Ta có:

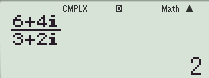
\(\begin{array}{l}\,\,\,\,\,\,\,\left( {3 + 2i} \right)z - \left( {4 + 9i} \right) = 2 - 5i\\ \Leftrightarrow \left( {3 + 2i} \right)z = 2 - 5i + 4 + 9i\\ \Leftrightarrow \left( {3 + 2i} \right)z = 6 + 4i\\ \Leftrightarrow z = \dfrac{{6 + 4i}}{{3 + 2i}} = 2\end{array}\)

Sử dụng MTCT:

MODE=>2 để chuyển sang chế độ số phức.

Cách ấn đơn vị ảo: nút ENG

Ta có \(z = m + 1 + mi \Rightarrow z - 2i = m + 1 + \left( {m - 2} \right)i.\)

\( \Rightarrow \left| {z - 2i} \right| = \sqrt {{{\left( {m + 1} \right)}^2} + {{\left( {m - 2} \right)}^2}} \).

Theo bài ra ta có: \(\left| {z - 2i} \right| > 1 \Rightarrow {\left( {m + 1} \right)^2} + {\left( {m - 2} \right)^2} > 1\)

\( \Leftrightarrow {m^2} + 2m + 1 + {m^2} - 4m + 4 > 1\) \( \Leftrightarrow 2{m^2} - 2m + 4 > 0\) (luôn đúng)

\( \Rightarrow m \in \mathbb{R}\).

Kết hợp điều kiện bài toán, ta có \(m \in \left( { - 5;5} \right),\,\,m \in \mathbb{Z}\)\( \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;0;1;2;3;4} \right\}.\)

Vậy có 9 giá trị của m thỏa mãn yêu cầu bài toán.

Ta có \(z = a + bi \Rightarrow \overline z  = a - bi\)

Khi đó

\(\begin{array}{l}\left( {1 + 2i} \right)z + \left( {3 - 4i} \right)\overline z  =  - 42 - 54i\\ \Leftrightarrow \left( {1 + 2i} \right)\left( {a + bi} \right) + \left( {3 - 4i} \right)\left( {a - bi} \right) =  - 42 - 54i\\ \Leftrightarrow \left( {4a - 6b} \right) + \left( { - 2a - 2b} \right)i =  - 42 - 54i\\ \Rightarrow \left\{ \begin{array}{l}4a - 6b =  - 42\\ - 2a - 2b =  - 54\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 12\\b = 15\end{array} \right.\\ \Rightarrow a + b = 27\end{array}\)

Số phức liên hợp của số phức \(3 - 2i\) là \(3 + 2i\).

\(z + w = \left( {1 + 2i} \right) + \left( {3 - 4i} \right) = \left( {1 + 3} \right) + \left( {2 - 4} \right)i = 4 - 2i\).

Ta có: \(z = \dfrac{i}{{1 + i}} = \dfrac{{i\left( {1 - i} \right)}}{{\left( {1 + i} \right)\left( {1 - i} \right)}}\)\( = \dfrac{{i - {i^2}}}{2} = \dfrac{{1 + i}}{2}\)

\( \Rightarrow \) Số phức liên hợp với số phức đã cho là: \(\overline z  = \dfrac{{1 - i}}{2}.\)

Phần thực của số phức \(z = 3 - 2i\)  bằng \(3\).

Ta có: \(z + {\rm{w}} = 3 + 2i + 1 - 4i = 4 - 2i\)

Sử dụng MTCT ta có:

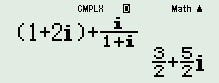
\( \Rightarrow z = \dfrac{3}{2} + \dfrac{5}{2}i\).

Vậy số phức \(z\) có phần thực bằng \(\dfrac{3}{2}\).

\(\dfrac{1}{z} = \dfrac{1}{{1 + \sqrt 3 i}} = \dfrac{1}{4} - \dfrac{{\sqrt 3 }}{4}i.\)