Số phức và các phép toán cộng, trừ, nhân, chia số phức

\(\begin{array}{l}\,\,\,\,\,\left( {3 + i} \right)z + \left( {4 - 5i} \right) = 6 - 3i\\ \Leftrightarrow \left( {3 + i} \right)z = 6 - 3i - \left( {4 - 5i} \right)\\ \Leftrightarrow \left( {3 + i} \right)z = 2 + 2i\\ \Leftrightarrow z = \dfrac{{2 + 2i}}{{3 + i}} = \dfrac{4}{5} + \dfrac{2}{5}i\end{array}\)

\(\begin{array}{l}\,\,\,\,\,\,\left( {1 + 3i} \right)z - 5 = 7i\\ \Leftrightarrow z = \dfrac{{7i + 5}}{{1 + 3i}} = \dfrac{{13}}{5} - \dfrac{4}{5}i\\ \Rightarrow \overline z  = \dfrac{{13}}{5} + \dfrac{4}{5}i\end{array}\)

Ta có \(iz = 3 + 2i \Rightarrow z = \dfrac{{3 + 2i}}{i} = 2 - 3i\)

Vậy \(z = 2 - 3i\) có số phức liên hợp là \(\overline z  = 2 + 3i\).

Ta có \(\dfrac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i \Rightarrow z = \dfrac{{\left( {2 + 3i} \right)\left( {1 - 2i} \right) - 2}}{{ - 1 + i}} =  - \dfrac{7}{2} - \dfrac{5}{2}i\)

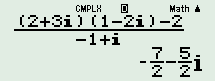
\(\begin{array}{l} \Rightarrow \overline z  =  - \dfrac{7}{2} + \dfrac{5}{2}i\\ \Rightarrow a =  - \dfrac{7}{2};\,\,b = \dfrac{5}{2}\end{array}\)

Vậy \(a + b =  - \dfrac{7}{2} + \dfrac{5}{2} =  - 1.\)

\({\rm{i}}{\rm{. }}\bar z = 5 + 2i \Leftrightarrow \bar z = \dfrac{{5 + 2i}}{i} = 2-5i\)\( \Rightarrow z = 2 + 5i\)

Phần ảo của z là 5.

Đặt \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi\).

Theo bài ra ta có: \(\left( {2 - i} \right)z + 3 + 16i = 2\left( {\overline z  + i} \right).\)

\(\begin{array}{l} \Leftrightarrow \left( {2 - i} \right)\left( {a + bi} \right) + 3 + 16i = 2\left( {a - bi + i} \right)\\ \Leftrightarrow 2a + 2bi - ai + b + 3 + 16i = 2a - 2bi + 2i\\ \Leftrightarrow \left\{ \begin{array}{l}2a + b + 3 = 2a\\2b - a + 16 =  - 2b + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 3\\4b - a =  - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 3\\a = 2\end{array} \right.\\ \Rightarrow z = 2 - 3i \Rightarrow \left| z \right| = \sqrt {{2^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {13} \end{array}\)

Ta có:

\(\begin{array}{l}z = {\left( {2i - 1} \right)^2} - {\left( {3 + i} \right)^2} = 4{i^2} - 4i + 1 - \left( {9 + 6i + {i^2}} \right)\\ =  - 4 - 4i + 1 - 9 - 6i - \left( { - 1} \right) =  - 11 - 10i\end{array}\) 

\( \Rightarrow z =  - 11 - 10i\) nên phần thực của \(z\) bằng \( - 11\) và phần ảo bằng \( - 10\).

Tổng phần thực và phần ảo là \(\left( { - 11} \right) + \left( { - 10} \right) =  - 21\).

Ta có \(3z - \left( {4 + 5i} \right)\overline z  =  - 17 + 11i\)\( \Leftrightarrow 3\left( {a + bi} \right) - \left( {4 + 5i} \right)\left( {a - bi} \right) =  - 17 + 11i\)

\(\begin{array}{l} \Leftrightarrow 3a + 3bi - 4a + 4bi - 5ai - 5b =  - 17 + 11i\\ \Leftrightarrow \left( { - a - 5b} \right) + \left( {7b - 5a} \right)i =  - 17 + 11i\\ \Leftrightarrow \left\{ \begin{array}{l} - a - 5b =  - 17\\7b - 5a = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\end{array}\)

Suy ra \(ab = 2.3 = 6\).

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\).

Xét đáp án A: \(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| {\overline z } \right| = \sqrt {{a^2} + {{\left( { - b} \right)}^2}} \) \( \Rightarrow \left| z \right| = \left| {\overline z } \right|\).

Xét đáp án B:

\(\begin{array}{l}z.\overline z  = \left( {a + bi} \right)\left( {a - bi} \right) = {a^2} - {\left( {bi} \right)^2} = {a^2} + {b^2}\\{\left| z \right|^2} = {a^2} + {b^2}\end{array}\)

\( \Rightarrow z.\overline z  = {\left| z \right|^2}\).

Xét đáp án C:

\(\dfrac{{z - \overline z }}{i} = \dfrac{{i\left( {z - \overline z } \right)}}{{{i^2}}} =  - i\left( {z - \overline z } \right)\) \( =  - i\left( {a + bi - a + bi} \right) =  - 2b{i^2} = 2b\) là số thực, không phải số thuần ảo.

Xét đáp án D: \(z + \overline z  = a + bi + a - bi = 2a\) là số thực.

Vậy chỉ có đáp án C sai.

Ta có \(\left( {3 - 2i} \right)\left( {x - yi} \right) - 4\left( {1 - i} \right) = \left( {2 + i} \right)\left( {x + yi} \right)\)

\(\begin{array}{l} \Leftrightarrow 3x - 3yi - 2xi - 2y - 4 + 4i = 2x + 2yi + xi - y\\ \Leftrightarrow \left( {3x - 2y - 4} \right) - \left( {3y + 2x - 4} \right)i = \left( {2x - y} \right) + \left( {2y + x} \right)i\\ \Leftrightarrow \left\{ \begin{array}{l}3x - 2y - 4 = 2x - y\\ - \left( {3y + 2x - 4} \right) = 2y + x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 4\\5y + 3x = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 1\end{array} \right.\end{array}\)

\(\begin{array}{l}\left( {2i - {i^2}} \right)z + 10i = 5\\ \Leftrightarrow z = \dfrac{{5 - 10i}}{{2i - {i^2}}}\\ \Leftrightarrow z =  - 3 - 4i.\end{array}\)

Số phức \(z =  - 3 - 4i\) có \({\mathop{\rm Re}\nolimits} z =  - 3,\,\,{\mathop{\rm Im}\nolimits} z =  - 4\), \(\left| z \right| = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 4} \right)}^2}}  = 4\) và \(\overline z  =  - 3 + 4i\).

Do đó chỉ có đáp án C sai.

Ta có:

\(\begin{array}{l}\dfrac{{\left( {1 - 3i} \right)\overline z }}{{{{\left| z \right|}^2}}} - 5i = \dfrac{{2 + i}}{z},\,\,\left( {z \ne 0} \right) \Leftrightarrow \dfrac{{\left( {1 - 3i} \right)\overline z }}{{\overline z .z}} - 5i = \dfrac{{2 + i}}{z}\\ \Leftrightarrow \left( {1 - 3i} \right) - 5iz = 2 + i \Leftrightarrow z =  - \dfrac{{1 + 4i}}{{5i}} \Leftrightarrow z =  - \dfrac{4}{5} + \dfrac{1}{5}i\end{array}\)

Suy ra phần ảo của số phức \(z\) là \(\dfrac{1}{5}\).

Phần thực của số phức \(z = 4 - 2i\) bằng \(4.\)

Phần thực của số phức \(z = 5 - 2i\)  bằng \(5\).

Ta có \(2a + \left( {b + i} \right)i = 1 + 2i \Leftrightarrow 2a + bi + {i^2} = 1 + 2i\)\( \Leftrightarrow 2a + b\) \( \Leftrightarrow 2a - 1 + bi = 1 + 2i \Leftrightarrow \left\{ \begin{array}{l}2a - 1 = 1\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\end{array} \right.\)

\(z + w = \left( {4 + 2i} \right) + \left( {3 - 4i} \right) = \left( {4 + 3} \right) + \left( {2 - 4} \right)i = 7 - 2i\).

Ta có: \(iz = 4 + 3i \Rightarrow z = 3 - 4i\)

Số phức liên hợp của \(z\) là \(\overline z  = 3 + 4i\)

Điểm \(M\left( {3; - 1} \right)\) là điểm biểu diễn số phức \(z = 3 - i.\)

Ta có:\(z = 3 + 2i \Rightarrow \overline z  = 3 - 2i.\)

Ta có: \(z = 4 - 3i\) có phần thực là \(4\) và phần ảo là \( - 3.\)