Phương trình \({7^{2{x^2} + 5x + 4}} = 49\) có tổng tất cả các nghiệm bằng
Ta có \({7^{2{x^2} + 5x + 4}} = 49 = {7^2} \Leftrightarrow 2{x^2} + 5x + 4 = 2 \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = - 2\end{array} \right.\).
Vậy tổng các nghiệm của phương trình là \( - \dfrac{1}{2} - 2 = \dfrac{{ - 5}}{2}\).
Đề thi THPT QG 2019 – mã đề 104
Nghiệm của phương trình \({2^{2x - 1}} = 32\) là
\({2^{2x - 1}} = 32 \Leftrightarrow 2x - 1 = {\log _2}32 = 5 \Leftrightarrow 2x = 6 \Leftrightarrow x = 3\).
Vậy nghiệm của phương trình là \(x = 3\).
Biết rằng tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \({(2 + \sqrt 3 )^x} + m{(2 - \sqrt 3 )^x} = 1\) có hai nghiệm phân biệt là khoảng \((a;b)\). Tính \(T = \) \(3a + 8b\).
Đặt \(t = {(2 + \sqrt 3 )^x},t > 0\)\( \Rightarrow {(2 - \sqrt 3 )^x} = \dfrac{1}{t}\).
Khi đó phương trình trở thành \(t + m \cdot \dfrac{1}{t} = 1\)\( \Leftrightarrow {t^2} + m = t \Leftrightarrow m = - {t^2} + t\)\( \Leftrightarrow m = f(t)\).
Bài toán tương đương: Tìm \(m\) để phương trình \(m = f(t)\) có hai nghiệm dương phân biệt.
Ta có \(f(t) = - {t^2} + t\)\( \Rightarrow {f^\prime }(t) = - 2t + 1;\)
\({f^\prime }(t) = 0 \Leftrightarrow t = \dfrac{1}{2} > 0\).
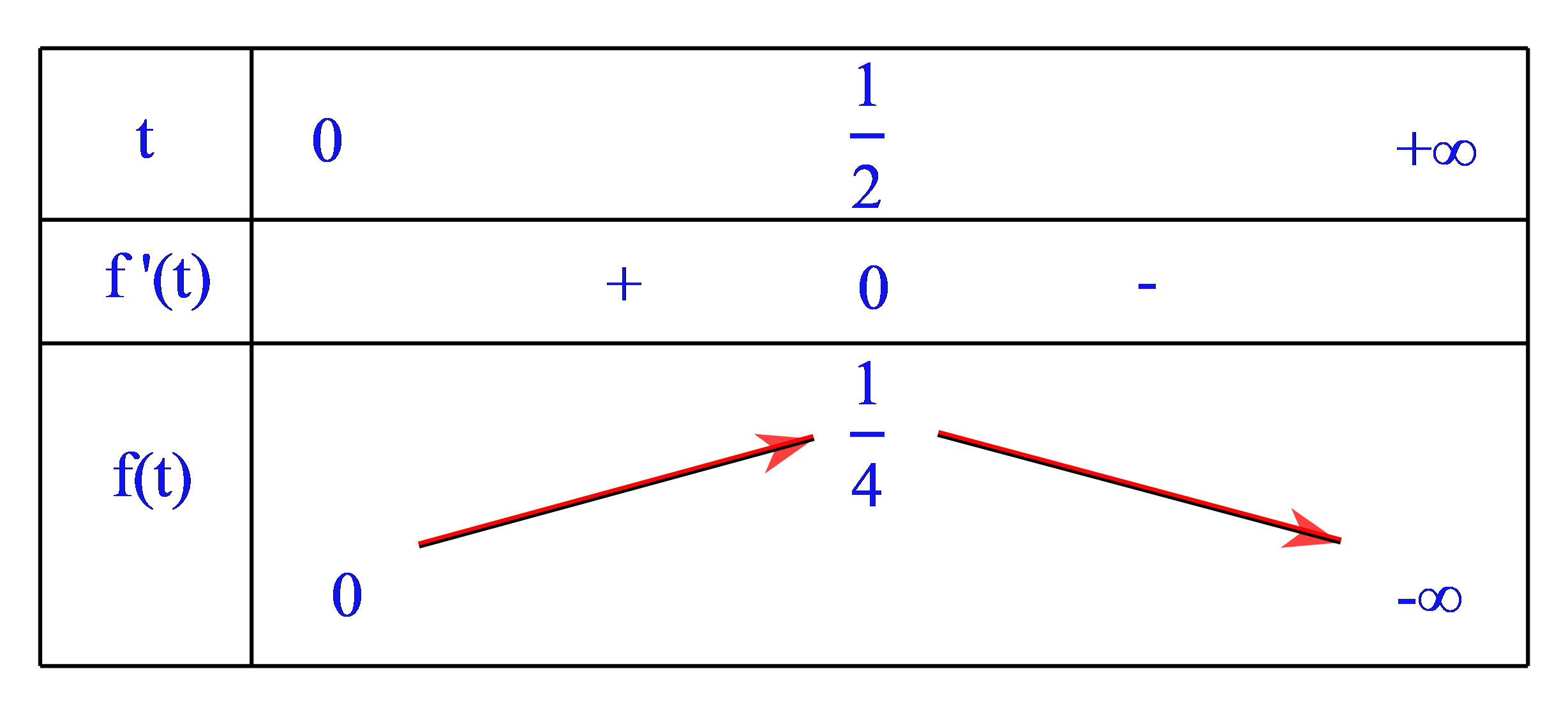
Dựa vào bảng biến thiên ta thấy phương trình có 2 nghiệm khi \(0 < m < \dfrac{1}{4}\).
Vậy \(m \in \left( {0;\dfrac{1}{4}} \right)\) từ đó ta có \(a = 0,b = \dfrac{1}{4}\)
\( \Rightarrow T = 3a + 8b = 2\).
Có bao nhiêu số nguyên \(y\) sao cho tồn tại \(x \in \left( {\dfrac{1}{3};5} \right)\) thỏa mãn \({27^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{15x}}\)
* pt \( \Leftrightarrow 27{\,^{3{x^2} + xy - 15x}} = xy + 1\).
\( \Rightarrow xy + 1 > 0 \Leftrightarrow y > - \dfrac{1}{x}\), khi \(x \in \left( {\dfrac{1}{3};5} \right)\) \( \Rightarrow y > - 3\) thì mới tồn tại \(x \in \left( {\dfrac{1}{3};5} \right)\).
\( \Rightarrow \) Ta chặn được \(y > - 3\) => \(y \ge - 2\).
* \(pt \Leftrightarrow {27^{3{x^2} + xy - 15x}} - xy - 1 = 0\).
Đặt \(f\left( x \right) = g\left( y \right) = {27^{3{x^2} + xy - 15x}} - xy - 1\) ta có \(\left\{ \begin{array}{l}f\left( {\dfrac{1}{3}} \right) = {3^{y - 14}} - \dfrac{y}{3} - 1\\f\left( 5 \right) = {27^{5y}} - 5y - 1\end{array} \right.\).
Nhận thấy ngay \(f\left( 5 \right) \ge 0\,\,\forall y \in \mathbb{Z}\), chỉ bằng 0 tại \(y = 0\).
+ Xét \(y = 0 \Rightarrow \) thay vào phương trình ban đầu \( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 5\end{array} \right.\), loại vì không có nghiệm thuộc \(\left( {\dfrac{1}{3};5} \right)\).
+ Xét \(y \ne 0 \Rightarrow f\left( 5 \right) > 0\,\,\forall x \in {\mathbb{Z}^*}\).
1) Ta Table khảo sát \(f\left( {\dfrac{1}{3}} \right)\) với \(\left\{ \begin{array}{l}Start:\,\,y = - 2\\End:\,\,y = 17\\Step:\,\,\, = 1\end{array} \right.\)
\( \Rightarrow f\left( {\dfrac{1}{3}} \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;15} \right\}\).
\( \Rightarrow f\left( {\dfrac{1}{3}} \right).f\left( 5 \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;15} \right\}\)
\( \Rightarrow \) Có 17 giá trị của \(y\) để tồn tại nghiệm \(x \in \left( {\dfrac{1}{3};5} \right)\).
2) Từ bảng Table ta nhận thấy khi \(y \ge 16\) thì \(f\left( {\dfrac{1}{3}} \right) > 0\) và đồng biến.
Ta đi chứng minh khi \(y \ge 16\) thì phương trình vô nghiệm.
\(g'\left( y \right) = x\left( {{{27}^{3{x^2} + x\left( {y - 15} \right)}}.\ln 27 - 1} \right) > 0\,\,\left\{ \begin{array}{l}\forall y \ge 16\\x \in \left( {\dfrac{1}{3};5} \right)\end{array} \right.\)
\( \Rightarrow g\left( y \right) \ge g\left( {16} \right) = {27^{3{x^2} + x}} - 16x - 1 = h\left( x \right)\).
Ta có \(h'\left( x \right) = {27^{3{x^2} + x}}\left( {6x + 1} \right)\ln 27 - 16 > 0\,\,\forall x \in \left( {\dfrac{1}{3};5} \right)\).
\( \Rightarrow h\left( x \right) > h\left( {\dfrac{1}{3}} \right) = \dfrac{8}{3} > 0\).
\( \Rightarrow \) Phương trình vô nghiệm với \(x \in \left( {\dfrac{1}{3};5} \right)\).
Vậy đáp số có 17 giá trị nguyên của \(y\).
Nếu \(a > 0,b > 0\) thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {a + b} \right)\) thì \(\dfrac{a}{b}\) bằng:
Ta có: \({\log _4}a = {\log _6}b = {\log _9}(a + b) = t\) suy ra \(\left\{ \begin{array}{l}a = {4^t}\\b = {6^t}\\a + b = {9^t}\end{array} \right.\)
\( \Rightarrow {4^t} + {6^t} = {9^t}\)\( \Leftrightarrow {\left( {\dfrac{2}{3}} \right)^{2t}} + {\left( {\dfrac{2}{3}} \right)^t} - 1 = 0\)
Đặt \({\left( {\dfrac{2}{3}} \right)^t} = u > 0 \Rightarrow {u^2} + u - 1 = 0\) \( \Rightarrow \left[ \begin{array}{l}u = \dfrac{{ - 1 + \sqrt 5 }}{2}\left( {tm} \right)\\u = \dfrac{{ - 1 - \sqrt 5 }}{2}\left( {ktm} \right)\end{array} \right.\)
Nên \({\left( {\dfrac{2}{3}} \right)^t} = \dfrac{{ - 1 + \sqrt 5 }}{2}\)
Mà \(\dfrac{a}{b} = \dfrac{{{4^t}}}{{{6^t}}} = {\left( {\dfrac{2}{3}} \right)^t}\) nên \(\dfrac{a}{b} = \dfrac{{ - 1 + \sqrt 5 }}{2}\)
Tổng bình phương các nghiệm của phương trình \({5^{3x - 2}} = {\left( {\dfrac{1}{5}} \right)^{ - {x^2}}}\) bằng
Ta có: \({5^{3x - 2}} = {\left( {\dfrac{1}{5}} \right)^{ - {x^2}}} \Leftrightarrow {5^{3x - 2}} = {5^{{x^2}}} \Leftrightarrow 3x - 2 = {x^2} \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Tổng bình phương các nghiệm của phương trình là \({1^2} + {2^2} = 5\).
Khi đặt \({3^x} = t\) thì phương trình \({9^{x + 1}} - {3^{x + 1}} - 30 = 0\) trở thành:
Ta có: \({9^{x + 1}} - {3^{x + 1}} - 30 = 0 \Leftrightarrow {9.9^x} - {3.3^x} - 30 = 0 \Leftrightarrow 3.{\left( {{3^x}} \right)^2} - {3^x} - 10 = 0\,\,\,\left( * \right)\)
Đặt \({3^x} = t\) ta có phương trình \(\left( * \right) \Leftrightarrow 3{t^2} - t - 10 = 0.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Có bao nhiêu số nguyên \(y\) sao cho tồn tại \(x \in \left( {\dfrac{1}{3};6} \right)\) thỏa mãn \({27^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{18x}}\)
Ta có: \({27^{3{x^2} + xy - 18x}} = xy + 1\)
ĐK: \(xy + 1 > 0 \Leftrightarrow y > - \dfrac{1}{x}\) khi \(x \in \left( {\dfrac{1}{3};6} \right)\)\( \Rightarrow y > - 3\) thì mới tồn tại \(x \in \left( {\dfrac{1}{3};6} \right)\).
Xét \({27^{3{x^2} + xy - 18x}} - xy - 1 = 0\)
Đặt \(f\left( x \right) = g\left( y \right) = {27^{3{x^2} + xy - 18x}} - xy - 1\) ta có: \(\left\{ \begin{array}{l}f\left( {\dfrac{1}{3}} \right) = {3^{y - 17}} - \dfrac{y}{3} - 1\\f\left( 6 \right) = {27^{6y}} - 6y - 1\end{array} \right.\)
Nhận thấy \(f\left( 6 \right) \ge 0\,\forall \,y \in \mathbb{Z}\). Dấu bằng xảy ra khi \(y = 0\).
Xét \(y = 0\) thay vào phương trình ban đầu \( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 6\end{array} \right.\) loại vì \(x \in \left( {\dfrac{1}{3};6} \right)\)
Xét \(y \ne 0 \Rightarrow f\left( 6 \right) > 0\,\forall \,x \in \mathbb{Z}*\)
Ta table khảo sát \(f\left( {\dfrac{1}{3}} \right)\) ta rút ra được \(f\left( {\dfrac{1}{3}} \right) < 0,\,\forall y \in \left\{ { - 2; - 1;1;2;...;17;18} \right\}\).
Ta có: \(f\left( {\dfrac{1}{3}} \right).f\left( 6 \right) < 0\,\forall \,y \in \left\{ { - 2; - 1;1;2;...;18} \right\}\)
Có \(20\) giá trị của \(y\) để tồn tại nghiệm \(x \in \left( {\dfrac{1}{3};6} \right)\)
Từ bảng Table ta nhận thấy khi \(y \ge 19\) thì phương trình vô nghiệm.
\(g'\left( y \right) = x\left( {{{27}^{3{x^2} + x\left( {y - 18} \right)}}.\ln 27 - 1} \right) > 0 \Rightarrow \left\{ \begin{array}{l}\forall y \ge 19\\x \in \left( {\dfrac{1}{3};6} \right)\end{array} \right.\)
Vậy có \(20\) giá trị nguyên của \(y\) thỏa mãn.
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \({2^{{{\sin }^2}x}} + {3^{{{\cos }^2}x}} = m \cdot {3^{{{\sin }^2}x}}\) có nghiệm?
Bước 1: Biến đổi \({\cos ^2}x = 1 - {\sin ^2}x\) và thay vào phương trình.
Ta có \({2^{{{\sin }^2}x}} + {3^{{{\cos }^2}x}} = m \cdot {3^{{{\sin }^2}x}} \Leftrightarrow {2^{{{\sin }^2}x}} + {3^{1 - {{\sin }^2}x}} = m \cdot {3^{{{\sin }^2}x}}\).
Bước 2: Đặt \(t = {\sin ^2}x,t \in [0;1]\). Chia cả 2 vế cho \({3^t}\)
Đặt \(t = {\sin ^2}x,t \in [0;1]\). Phương trình đã cho trở thành
\({2^t} + {3^{1 - t}} = m{.3^t} \Leftrightarrow {\left( {\dfrac{2}{3}} \right)^t} + {3^{1 - 2t}} = m\)
Bước 3: Xét hàm số \(f(t) = {\left( {\dfrac{2}{3}} \right)^t} + {3^{1 - 2t}}\), với \(t \in [0;1]\). Tìm m.
Xét hàm số \(f(t) = {\left( {\dfrac{2}{3}} \right)^t} + {3^{1 - 2t}}\), với \(t \in [0;1]\). Ta có \(f'(t) = {\left( {\dfrac{2}{3}} \right)^t}.\ln \dfrac{2}{3} - {2.3^{1 - 2t}}.\ln 3\) \(f''(t) = {\left( {\dfrac{2}{3}} \right)^t} \cdot {\left( {\ln \dfrac{2}{3}} \right)^2} + {4.3^{1 - 2t}} \cdot {(\ln 3)^2} > 0\)\(\forall t \in \left[ {0;1} \right]\)
\( \Rightarrow {f^\prime }(t)\) liên tục và đồng biến trên [0 ; 1] nên \({f^\prime }(t) \le {f^\prime }(1) = \dfrac{2}{3}\ln \dfrac{2}{9} < 0,\forall t \in [0;1]\).
\( \Rightarrow {f^\prime }(t)<0\forall t \in [0;1]\)
\( \Rightarrow f(t)\) liên tục và nghịch biến trên [0 ; 1] nên \(f(1) \le f(t) \le f(0),\forall t \in [0;1]\)
Suy ra \(1 \le m \le 4\).
Vậy có 4 giá trị m thỏa mãn.
Tính tích các nghiệm của phương trình \({9^x} - {3^{x + 1}} + 2 = 0\)
Ta có \({9^x} - {3^{x + 1}} + 2 = 0 \Leftrightarrow {3^{2x}} - {3.3^x} + 2 = 0\)
Đặt \({3^x} = t > 0\) ta có phương trình \({t^2} - 3t + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}{3^x} = 1\\{3^x} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = {\log _3}2\end{array} \right.\)
Nên tích các nghiệm của phương trình là \(0.{\log _3}2 = 0\)
Tính tổng tất cả các nghiệm của phương trình \({8^{2x + \dfrac{1}{3}}} - {5.8^x} + 2 = 0\).
Bước 1: Sử dụng công thức \({a^{m + n}} = {a^m}.{a^n}\)
\(\begin{array}{l}{8^{2x + \dfrac{1}{3}}} - {5.8^x} + 2 = 0\\ \Leftrightarrow {8^{2x}}{.8^{\dfrac{1}{3}}} - {5.8^x} + 2 = 0\end{array}\)
Bước 2: Giải phương trình và tính tổng nghiệm
\(\begin{array}{l} \Leftrightarrow 2.{\left( {{8^x}} \right)^2} - {5.8^x} + 2 = 0\\ \Leftrightarrow 2.{\left( {{8^x}} \right)^2} - {4.8^x} - {8^x} + 2 = 0\\ \Leftrightarrow {2.8^x}.\left( {{8^x} - 2} \right) - \left( {{8^x} - 2} \right) = 0\\ \Leftrightarrow \left( {{8^x} - 2} \right)\left( {{{2.8}^x} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{8^x} = 2\\{8^x} = \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{3}\\x = - \dfrac{1}{3}\end{array} \right.\end{array}\)
Tổng nghiệm bằng 0
Giải phương trình \({9^{\left| {x + 1} \right|}} = {27^{2x - 2}}.\) Ta có tập nghiệm bằng:
\(\begin{array}{l}{9^{\left| {x + 1} \right|}} = {27^{2x - 2}} \Leftrightarrow {3^{2\left| {x + 1} \right|}} = {3^{3\left( {2x - 2} \right)}} \Leftrightarrow 2\left| {x + 1} \right| = 6x - 6\\ \Leftrightarrow \left[ \begin{array}{l}2x + 2 = 6x - 6\,\,khi\,x \ge - 1\\2x + 2 = - 6x + 6\,\,khi\,x < - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = \dfrac{1}{2}\,\,\left( {ktm} \right)\end{array} \right..\end{array}\)
Số nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) là:
\({2^{2{x^2} - 7x + 5}} = 1 \Leftrightarrow {2^{2{x^2} - 7x + 5}} = {2^0} \Leftrightarrow 2{x^2} - 7x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{5}{2}\end{array} \right..\)
Vậy phương trình đã cho có 2 nghiệm
Nghiệm của phương trình \({\left( {\dfrac{1}{{25}}} \right)^{x + 1}} = {125^{2x}}\) là:
\({\left( {\dfrac{1}{{25}}} \right)^{x + 1}} = {125^{2x}}\) \( \Leftrightarrow {\left( {{5^{ - 2}}} \right)^{x + 1}} = {\left( {{5^3}} \right)^{2x}} \) \(\Leftrightarrow {5^{ - 2x - 2}} = {5^{6x}}\) \( \Leftrightarrow - 2x - 2 = 6x \Leftrightarrow x = - \dfrac{1}{4}.\)
Tích các nghiệm của phương trình \({\left( {2 + \sqrt 3 } \right)^x} + {\left( {2 - \sqrt 3 } \right)^x} = 14\) là:
Ta có: \(\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right) = {2^2} - {\left( {\sqrt 3 } \right)^2} = 1 \) \(\Leftrightarrow {\left( {2 + \sqrt 3 } \right)^x}{\left( {2 - \sqrt 3 } \right)^x} = 1\) \( \Leftrightarrow {\left( {2 - \sqrt 3 } \right)^x} = \dfrac{1}{{{{\left( {2 + \sqrt 3 } \right)}^x}}} = {\left( {2 + \sqrt 3 } \right)^{ - x}},\)
Khi đó phương trình có dạng \({\left( {2 + \sqrt 3 } \right)^x} + {\left( {2 + \sqrt 3 } \right)^{ - x}} = 14.\)
Đặt \({\left( {2 + \sqrt 3 } \right)^x} = t\,\,\left( {t > 0} \right),\) phương trình trở thành \(\begin{array}{l}t + {t^{ - 1}} = 14 \Leftrightarrow t + \dfrac{1}{t} = 14 \Leftrightarrow {t^2} - 14t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}{t_1} = 7 + 4\sqrt 3 = {\left( {2 + \sqrt 3 } \right)^2}\\{t_2} = 7 - 4\sqrt 3 = {\left( {2 - \sqrt 3 } \right)^2} = {\left( {2 + \sqrt 3 } \right)^{ - 2}}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\left( {2 + \sqrt 3 } \right)^x} = {\left( {2 + \sqrt 3 } \right)^2}\\{\left( {2 + \sqrt 3 } \right)^x} = {\left( {2 + \sqrt 3 } \right)^{ - 2}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} = 2\\{x_2} = - 2\end{array} \right. \Rightarrow {x_1}{x_2} = - 4.\end{array}\)
Biết rằng tập hợp các giá trị của \(m\) để phương trình \({\left( {\dfrac{1}{4}} \right)^{{x^2}}} - \left( {m + 1} \right).{\left( {\dfrac{1}{2}} \right)^{{x^2}}} - 2m = 0\) có nghiệm, là \(\left[ { - a + 2\sqrt b ;0} \right]\) với \(a,b\) là các số nguyên dương. Tính \(b - a\).
Đặt \(t = {\left( {\dfrac{1}{2}} \right)^{{x^2}}} \Rightarrow 0 < t \le 1\) thì phương trình trở thành \({t^2} - \left( {m + 1} \right)t - 2m = 0 \Leftrightarrow {t^2} - t = mt + 2m \Leftrightarrow \dfrac{{{t^2} - t}}{{t + 2}} = m\)
Để phương trình đã cho có nghiệm thì đường thẳng \(y = m\) phải cắt đồ thị hàm số \(y = f\left( t \right) = \dfrac{{{t^2} - t}}{{t + 2}}\) tại ít nhất một điểm \(t \in \left( {0;1} \right]\).
Xét \(f\left( t \right) = \dfrac{{{t^2} - t}}{{t + 2}}\) trên \(\left( {0;1} \right]\) có \(f'\left( t \right) = \dfrac{{{t^2} + 4t - 2}}{{{{\left( {t + 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 2 + \sqrt 6 \in \left( {0;1} \right]\\t = - 2 - \sqrt 6 \notin \left( {0;1} \right]\end{array} \right.\)
Ta có : \(f\left( 0 \right) = 0,f\left( 1 \right) = 0,f\left( { - 2 + \sqrt 6 } \right) = - 5 + 2\sqrt 6 \) \( \Rightarrow \mathop {\max }\limits_{\left( {0;1} \right]} f\left( t \right) = 0,\mathop {\min }\limits_{\left( {0;1} \right]} f\left( t \right) = - 5 + 2\sqrt 6 \).
Vậy phương trình có nghiệm nếu \( - 5 + 2\sqrt 6 \le m \le 0 \Rightarrow m \in \left[ { - 5 + 2\sqrt 6 ;0} \right]\) hay \(a = 5,b = 6 \Rightarrow b - a = 1\).
Có bao nhiêu số nguyên \(m\) thuộc \(\left[ { - 2020;2020} \right]\) sao cho phương trình \({4^{{{\left( {x - 1} \right)}^2}}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\) có bốn nghiệm phân biệt?
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,{4^{{{\left( {x - 1} \right)}^2}}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\\ \Leftrightarrow {4^{{x^2} - 2x + 1}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\\ \Leftrightarrow {4.4^{{x^2} - 2x}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\end{array}\)
Đặt \(t = {2^{{x^2} - 2x}}\). Ta có: \({x^2} - 2x = {\left( {x - 1} \right)^2} - 1 \ge - 1\) \( \Rightarrow t \ge {2^{ - 1}} = \dfrac{1}{2}\).
Khi đó phương trình trở thành \(4{t^2} - 4m.t + 3m - 2 = 0\,\,\,\left( * \right)\) với \(t \ge \dfrac{1}{2}\).
Để phương trình ban đầu có 4 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm \(t\) phân biệt thỏa mãn \(t > \dfrac{1}{2}\).
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{t_1} + {t_2} > 1\\\left( {{t_1} - \dfrac{1}{2}} \right)\left( {{t_2} - \dfrac{1}{2}} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 4\left( {3m - 2} \right) > 0\\m > 0\\\dfrac{{3m - 2}}{4} - \dfrac{1}{2}.m + \dfrac{1}{4} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 8 > 0\\m > 0\\3m - 2 - 2m + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\\m > 0\\m > 1\end{array} \right. \Leftrightarrow m > 2\end{array}\)
Kết hợp điều kiện đề bài ta có \(m \in \left( {2;2020} \right]\).
Vậy có \(2020 - 3 + 1 = 2018\) giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Tích các nghiệm của phương trình \({\left( {3 + \sqrt 5 } \right)^x} + {\left( {3 - \sqrt 5 } \right)^x} = {3.2^x}\) là:
\({\left( {3 + \sqrt 5 } \right)^x} + {\left( {3 - \sqrt 5 } \right)^x} = {3.2^x} \Leftrightarrow \dfrac{{{{\left( {3 + \sqrt 5 } \right)}^x}}}{{{2^x}}} + \dfrac{{{{\left( {3 - \sqrt 5 } \right)}^x}}}{{{2^x}}} = 3 \Leftrightarrow {\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^x} + {\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right)^x} = 3.\)
Ta có $\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right) = \dfrac{{{3^2} - {{\left( {\sqrt 5 } \right)}^2}}}{4} = 1 \Rightarrow {\left( {\dfrac{{3 - \sqrt 5 }}{2}} \right)^x} = \dfrac{1}{{{{\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)}^x}}} = {\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{ - x}}.$khi đó phương trình tương đương với \({\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^x} + {\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{ - x}} = 3.\)
Đặt \({\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^x} = t\,\,\left( {t > 0} \right)\), khi đó phương trình trở thành \(t + \dfrac{1}{t} = 3 \Leftrightarrow {t^2} - 3t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}{t_1} = \dfrac{{3 + \sqrt 5 }}{2}\\{t_2} = \dfrac{{3 - \sqrt 5 }}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^x} = \dfrac{{3 + \sqrt 5 }}{2}\\{\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^x} = \dfrac{{3 - \sqrt 5 }}{2} = {\left( {\dfrac{{3 + \sqrt 5 }}{2}} \right)^{ - 1}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 1\end{array} \right. \Rightarrow {x_1}{x_2} = - 1.\)
Có bao nhiêu số nguyên \(m\) thuộc \(\left[ { - 2020;2020} \right]\) sao cho phương trình \({4^{{{\left( {x - 1} \right)}^2}}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\) có bốn nghiệm phân biệt?
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,{4^{{{\left( {x - 1} \right)}^2}}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\\ \Leftrightarrow {4^{{x^2} - 2x + 1}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\\ \Leftrightarrow {4.4^{{x^2} - 2x}} - 4m{.2^{{x^2} - 2x}} + 3m - 2 = 0\end{array}\)
Đặt \(t = {2^{{x^2} - 2x}}\). Ta có: \({x^2} - 2x = {\left( {x - 1} \right)^2} - 1 \ge - 1\) \( \Rightarrow t \ge {2^{ - 1}} = \dfrac{1}{2}\).
Khi đó phương trình trở thành \(4{t^2} - 4m.t + 3m - 2 = 0\,\,\,\left( * \right)\) với \(t \ge \dfrac{1}{2}\).
Để phương trình ban đầu có 4 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm \(t\) phân biệt thỏa mãn \(t > \dfrac{1}{2}\).
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{t_1} + {t_2} > 1\\\left( {{t_1} - \dfrac{1}{2}} \right)\left( {{t_2} - \dfrac{1}{2}} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 4\left( {3m - 2} \right) > 0\\m > 0\\\dfrac{{3m - 2}}{4} - \dfrac{1}{2}.m + \dfrac{1}{4} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 8 > 0\\m > 0\\3m - 2 - 2m + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\\m > 0\\m > 1\end{array} \right. \Leftrightarrow m > 2\end{array}\)
Kết hợp điều kiện đề bài ta có \(m \in \left( {2;2020} \right]\).
Vậy có \(2020 - 3 + 1 = 2018\) giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Tìm m để phương trình \({4^{\sqrt {x + 1} + \sqrt {3 - x} }} - {14.2^{\sqrt {x + 1} + \sqrt {3 - x} }} + 8 = m\) có nghiệm
Điều kiện: \(\left\{ \begin{array}{l}x + 1 \ge 0\\3 - x \ge 0\end{array} \right. \Leftrightarrow - 1 \le x \le 3.\)
Đặt \(t = {2^{\sqrt {x + 1} + \sqrt {3 - x} }} = t(x)\,\,\left( {t\left( x \right) > 0} \right)\).Ta có \(t'\left( x \right) = \left( {\dfrac{1}{{2\sqrt {x + 1} }} - \dfrac{1}{{2\sqrt {3 - x} }}} \right){.2^{\sqrt {x + 1} + \sqrt {3 - x} }}\ln 2.\)
$ \Rightarrow t'(x) = 0 \Leftrightarrow \dfrac{1}{{2\sqrt {x + 1} }} - \dfrac{1}{{2\sqrt {3 - x} }} \Leftrightarrow \sqrt {x + 1} = \sqrt {3 - x} \Leftrightarrow x = 1.$
Bảng biến thiên
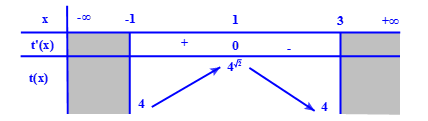
Do đó $t \in \left[ {4;{4^{\sqrt 2 }}} \right]$.
Yêu cầu bài toán trở thành: Tìm m để phương trình \({t^2} - 14t + 8 = m\,\,(*)\) có nghiệm với $t \in \left[ {4;{4^{\sqrt 2 }}} \right]$.
Xét hàm số \(g(t) = {t^2} - 14t + 8,\,\,t \in \left[ {4;{4^{\sqrt 2 }}} \right].\)
Ta có \(g'(t) = 2t - 14,\,\,g'(t) = 0 \Leftrightarrow 2t - 14 = 0 \Leftrightarrow t = 7\)
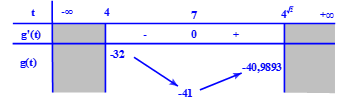
Dựa vào bảng biến thiên ta được giá trị m cần tìm là \( - 41 \le m \le - 32.\)

