Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 2,\,\,\left| {{z_2}} \right| = \sqrt 3 \). Gọi M, N là các điểm biểu diễn cho \({z_1}\) và \(i{z_2}\). Biết \(\widehat {MON} = {30^0}\). Tính \(S = \left| {z_1^2 + 4z_2^2} \right|\) ?
Đặt \({z_3} = i{z_2} \Rightarrow z_3^2 = - z_2^2 \Rightarrow S = \left| {z_1^2 + 4z_2^2} \right| = \left| {z_1^2 - 4z_3^2} \right| = \left| {{z_1} - 2{z_3}} \right|\left| {{z_1} + 2{z_3}} \right|\)
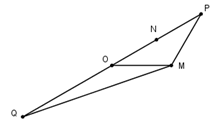
M, N là các điểm biểu diễn cho \({z_1},{z_3} \Rightarrow OM = 2,\,\,ON = \left| {{z_3}} \right| = \left| {i{z_2}} \right| = \left| i \right|.\left| {{z_2}} \right| = \sqrt 3 \).
Gọi P là điểm biểu diễn cho \(2{z_3}\) và \(Q\) là điểm biểu diễn cho \( - 2{z_3}\) , ta có N là trung điểm của OP và P, Q đối xứng nhau qua O. Khi đó \(S = MP.MQ\).
Áp dụng định lí Cosin trong \(\Delta OMP\) có:
\(M{P^2} = O{P^2} + O{M^2} - 2OP.OM.\cos 30 = 12 + 4 - 2.2\sqrt 3 .2.\dfrac{{\sqrt 3 }}{2} = 4 \Rightarrow MP = 2\)Áp dụng định lí Cosin trong \(\Delta OMQ\) có:
\(\begin{array}{l}M{Q^2} = O{M^2} + O{Q^2} - 2OM.OQ.\cos {150^0}\\\,\,\,\,\,\,\,\,\,\,\,\, = 4 + 12 + 2.2.2\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = 2\sqrt 7 \\ \Rightarrow S = MP.MQ = 2.2\sqrt 7 = 4\sqrt 7 \end{array}\)
Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} + 1 - i} \right| = 2\) và \({z_2} = i{z_1}\). Tìm giá trị lớn nhất m của biểu thức \(\left| {{z_1} - {z_2}} \right|\).
Ta có : \(2 = \left| {{z_1} + 1 - i} \right| = \left| {{z_1} + \left( {1 - i} \right)} \right|\)\( \ge \left| {{z_1}} \right| - \left| {1 - i} \right| = \left| {{z_1}} \right| - \sqrt 2 \)\( \Rightarrow \left| {{z_1}} \right| - \sqrt 2 \le 2 \Rightarrow \left| {{z_1}} \right| \le 2 + \sqrt 2 \)
Lại có \({z_2} = i{z_1} \Rightarrow \left| {{z_1} - {z_2}} \right| = \left| {{z_1} - i{z_1}} \right|\)\( = \left| {\left( {1 - i} \right){z_1}} \right| = \sqrt 2 \left| {{z_1}} \right|\)\( \le \sqrt 2 \left( {2 + \sqrt 2 } \right) = 2\sqrt 2 + 2\)
\( \Rightarrow \max \left| {{z_1} - {z_2}} \right| = 2\sqrt 2 + 2\)
Cho hai số phức ${z_1},\,{z_2}$ thỏa mãn $\left| {{z_1} + 1 - i} \right| = 2$ và ${z_2} = i{z_1}$. Tìm GTNN m của biểu thức $\left| {{z_1} - {z_2}} \right|$?
\(\begin{array}{l}
2 = \left| {{z_1} + 1 - i} \right| \le \left| {{z_1}} \right| + \left| {1 - i} \right| = \left| {{z_1}} \right| + \sqrt 2 \\
\Rightarrow \left| {{z_1}} \right| + \sqrt 2 \ge 2\\
\Rightarrow \left| {{z_1}} \right| \ge 2 - \sqrt 2 \\
\Rightarrow \left| {{z_1} - {z_2}} \right| = \left| {{z_1} - i{z_1}} \right|\\
= \left| {{z_1}\left( {1 - i} \right)} \right| = \left| {{z_1}} \right|.\sqrt 2 \\
\ge \left( {2 - \sqrt 2 } \right).\sqrt 2 = 2\sqrt 2 - 2\\
\Rightarrow \left| {{z_1} - {z_2}} \right| \ge 2\sqrt 2 - 2\\
\Rightarrow m = 2\sqrt 2 - 2
\end{array}\)
Cho các số phức ${z_1},\,{z_2},\,{z_3}$ thỏa mãn điều kiện $\left| {{z_1}} \right| = 4,\left| {{z_2}} \right| = 3,\,\left| {{z_3}} \right| = 2$ và $\left| {4{z_1}{z_2} + 16{z_2}{z_3} + 9{z_1}{z_3}} \right| = 48$. Giá trị của biểu thức $P = \left| {{z_1} + {z_2} + {z_3}} \right|$ bằng
Ta có: $\left| {4{z_1}{z_2} + 16{z_2}{z_3} + 9{z_1}{z_3}} \right| = \left| {{z_3}.\overline {{z_3}} .{z_1}{z_2} + {z_1}.\overline {{z_1}} .{z_2}{z_3} + {z_2}.\overline {{z_2}} .{z_1}{z_3}} \right| = \left| {{z_1}{z_2}{z_3}.\left( {\overline {{z_1}} + \overline {{z_2}} + \overline {{z_3}} } \right)} \right| = \left| {{z_1}{z_2}{z_3}} \right|.\left| {\overline {{z_1}} + \overline {{z_2}} + \overline {{z_3}} } \right|$
$ = \left| {{z_1}} \right|.\left| {{z_2}} \right|.\left| {{z_2}} \right|.\left| {\overline {{z_1} + {z_2} + {z_3}} } \right| = 24.\left| {{z_1} + {z_2} + {z_3}} \right| = 48$
$ \Rightarrow P = \left| {{z_1} + {z_2} + {z_3}} \right| = \dfrac{{48}}{{24}} = 2$
Có bao nhiêu số phức \(z\) thỏa mãn \(\left| z \right|\left( {z - 5 - i} \right) + 2i = \left( {6 - i} \right)z?\)
Ta có: \(\left| z \right|\left( {z - 5 - i} \right) + 2i = \left( {6 - i} \right)z\)
\( \Leftrightarrow \left| z \right|.z - 5\left| z \right| - \left| z \right|i + 2i = \left( {6 - i} \right)z \Leftrightarrow z\left( {\left| {z } \right|} - 6 + i \right) = 5\left| z \right| + \left( {\left| z \right| - 2} \right)i\;\;\;\left( * \right)\)
Lấy modul 2 vế của phương trình \(\left( * \right)\) ta được: \(\left| z \right|\sqrt {{{\left( {\left| z \right| - 6} \right)}^2} + 1} = \sqrt {25\left| {{z^2}} \right| + {{\left( {\left| z \right| - 2} \right)}^2}} \;\;\;\;\left( 1 \right)\)
Đặt \(x = \left| z \right|\;\;\left( {x \ge 0} \right).\) Khi đó ta có:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow x\sqrt {{{\left( {x - 6} \right)}^2} + 1} = \sqrt {25{x^2} + {{\left( {x - 2} \right)}^2}} \\ \Leftrightarrow {x^2}\left( {{x^2} - 12x + 36 + 1} \right) = 25{x^2} + {x^2} - 4x + 4\\ \Leftrightarrow {x^4} - 12{x^3} + 36{x^2} + {x^2} = 26{x^2} - 4x + 4\\ \Leftrightarrow {x^4} - 12{x^3} + 11{x^2} + 4x - 4 = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} - 11{x^2} + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\{x^3} - 11{x^2} + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\;\;\left( {tm} \right)\\x \approx 10,97\;\;\;\left( {tm} \right)\\x \approx 0,62\;\;\;\left( {tm} \right)\\x \approx - 0,59\;\;\;\left( {ktm} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| z \right| = 1\;\\\left| z \right| \approx 10,97\;\\\left| z \right| \approx 0,62\;\end{array} \right..\end{array}\)
Thay các \(\left| z \right|\) vào phương trình đã cho ta sẽ nhận được 3 số phức \(z\) thỏa mãn yêu cầu bài toán.
Cho \({z_1};{z_2};{z_3}\) là ba số phức thay đổi thỏa mãn $\left| {{z_1}} \right| = 2;\,\,\left| {{z_3}} \right| = 1$ và \({z_2} = {z_1}{z_3}\). Trong mặt phẳng phức A, B biểu diễn \({z_1};{z_2}\). Giả sử O, A, B lập thành tam giác có diện tích là a, chu vi là b. Giá trị lớn nhất của biểu thức \(T = a + b\) là:
Ta có \(\left| {{z_2}} \right| = \left| {{z_1}} \right|\left| {{z_3}} \right| = 2 \Rightarrow OB = OA = 2\).
Đặt \(AB = x\,\,\left( {0 < x < 4} \right)\) ta có: \(a = \dfrac{1}{2}.x.\sqrt {4 - \dfrac{{{x^2}}}{4}} = \dfrac{1}{4}x\sqrt {16 - {x^2}} ;\,\,b = 2 + 2 + x = 4 + x\)
\( \Rightarrow T = a + b = \dfrac{{x\sqrt {16 - {x^2}} }}{4} + 4 + x\)
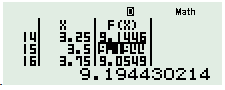
Sử dụng MTCT ta tính được \({T_{\max }} \approx 9,19\)
Cho các số phức \({z_1};{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 3;\,\,\left| {{z_2}} \right| = 4\) và chúng được biểu diễn trong mặt phẳng phức lần lượt là các điểm M, N. Biết góc giữa vector \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \) bằng \(60^0\). Tìm môđun của số phức \(z = \dfrac{{{z_1} + {z_2}}}{{{z_1} - {z_2}}}\) ?
Ta có \(OM = 3;\,\,ON = 4\) ; \(\widehat {\left( {\overrightarrow {OM} ;\overrightarrow {ON} } \right)} = {60^0} \Rightarrow \widehat {\left( {OM;ON} \right)} = {60^0}\).
\(\left| z \right| = \dfrac{{\left| {{z_1} + {z_2}} \right|}}{{\left| {{z_1} - {z_2}} \right|}} = \dfrac{{\left| {\overrightarrow {OM} + \overrightarrow {ON} } \right|}}{{\left| {\overrightarrow {OM} - \overrightarrow {ON} } \right|}} = \dfrac{{2\left| {\overrightarrow {OI} } \right|}}{{\left| {\overrightarrow {MN} } \right|}} = \dfrac{{2OI}}{{MN}}\) (với I là trung điểm của MN).
Áp dụng định lí cosin trong tam giác OMN có \(MN = \sqrt {O{M^2} + O{N^2} - 2OM.ON.\cos \left( {OM;ON} \right)} = \sqrt {13} \)
OI là đường trung tuyến của tam giác OMN \( \Rightarrow OI = \sqrt {\dfrac{{O{M^2} + O{N^2}}}{2} - \dfrac{{M{N^2}}}{4}} = \dfrac{{\sqrt {37} }}{2}\)
Vậy \(\left| z \right| = \dfrac{{2.\dfrac{{\sqrt {37} }}{2}}}{{\sqrt {13} }} = \dfrac{{\sqrt {481} }}{{13}}\).
Xét số phức z thỏa mãn \(\left( {1 + 2i} \right)\left| z \right| = \dfrac{{\sqrt {10} }}{z} - 2 + i\). Mệnh đề nào dưới đây đúng?
\(\begin{array}{l}\,\,\,\,\,\left( {1 + 2i} \right)\left| z \right| = \dfrac{{\sqrt {10} }}{z} - 2 + i\\ \Leftrightarrow \left( {1 + 2i} \right)\left| z \right| + 2 - i = \dfrac{{\sqrt {10} }}{z}\\ \Leftrightarrow \left( {\left| z \right| + 2} \right) + \left( {2\left| z \right| - 1} \right)i = \dfrac{{\sqrt {10} }}{z}\\ \Leftrightarrow {\left( {\left| z \right| + 2} \right)^2} + {\left( {2\left| z \right| - 1} \right)^2} = \dfrac{{10}}{{{{\left| z \right|}^2}}}\\ \Leftrightarrow {\left| z \right|^2} + 4\left| z \right| + 4 + 4{\left| z \right|^2} - 4\left| z \right| + 1 = \dfrac{{10}}{{{{\left| z \right|}^2}}}\\ \Leftrightarrow 5{\left| z \right|^4} + 5{\left| z \right|^2} - 10 = 0 \Leftrightarrow \left| z \right| = 1 \in \left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\end{array}\)
Xét các số phức \(z = a + bi,\,\,\left( {a;b \in R} \right)\) thỏa mãn đồng thời hai điều kiện \(\left| z \right| = \left| {\overline z + 4 - 3i} \right|\) và \(\left| {z + 1 - i} \right| + \left| {z - 2 + 3i} \right|\) đạt giá trị nhỏ nhất. Giá trị \(P = a + 2b\) là:
Gọi \(z = x + yi\) ta có:
\(\begin{array}{l}\left| {x + yi} \right| = \left| {x - yi + 4 - 3i} \right|\\ \Leftrightarrow {x^2} + {y^2} = {\left( {x + 4} \right)^2} + {\left( {y + 3} \right)^2}\\ \Leftrightarrow 8x + 6y = - 25\end{array}\)
Gọi điểm \(M\left( {x;y} \right)\) là điểm biểu diễn cho số phức z và \(A\left( { - 1;1} \right);\,\,B\left( {2; - 3} \right)\) ta có:
\(\left| {z + 1 - i} \right| + \left| {z - 2 + 3i} \right| = MA + MB\) nhỏ nhất.
Ta có : \(MA + MB \ge 2\sqrt {MA.MB} \), dấu bằng xảy ra \( \Leftrightarrow MA = MB \Rightarrow \) M thuộc trung trực của AB.
Gọi \(I\) là trung điểm của AB ta có \(I\left( {\dfrac{1}{2}; - 1} \right)\) và \(\overrightarrow {AB} = \left( {3; - 4} \right)\).
Phương trình đường trung trực của AB là \(3\left( {x - \dfrac{1}{2}} \right) - 4\left( {y + 1} \right) = 0 \Leftrightarrow 3x - 4y - \dfrac{{11}}{2} = 0\)
Để \({\left( {MA + MB} \right)_{\min }} \Leftrightarrow \) Tọa độ điểm M là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}8x + 6y = - 25\\3x - 4y = \dfrac{{11}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{{67}}{{50}}\\y = - \dfrac{{119}}{{50}}\end{array} \right.\)
\( \Rightarrow z = - \dfrac{{67}}{{50}} - \dfrac{{119}}{{50}}i \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{{67}}{{50}}\\b = - \dfrac{{119}}{{50}}\end{array} \right. \Rightarrow P = a + 2b = - \dfrac{{61}}{{10}}\)
Giả sử \({z_1},\,\,{z_2}\) là hai trong số các số phức \(z\) thỏa mãn \(\left| {iz + \sqrt 2 - i} \right| = 1\) và \(\left| {{z_1} - {z_2}} \right| = 2.\) Giá trị lớn nhất của \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\) bằng
Ta có: $\left| {iz + \sqrt 2 - i} \right| = 1 \Leftrightarrow \left| {i\left( {x + yi} \right) + \sqrt 2 - i} \right| = 1$ (với $z = x + yi\;\left( {x;y \in R} \right)$)
$ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - \sqrt 2 } \right)^2} = 1 \Rightarrow M\left( {x;y} \right)$ biểu diễn $z$ thuộc đường tròn tâm $I\left( {1;\sqrt 2 } \right)$ bán kính $R = 1.$
Giả sử $A\left( {{z_1}} \right);B\left( {{z_2}} \right)$ do $\left| {{z_1} - {z_2}} \right| = 2 \Rightarrow AB = 2 = 2R$ nên $AB$ là đường kính của đường tròn $\left( {I;R} \right)$
Lại có: $\left| {{z_1}} \right| + \left| {{z_2}} \right| = OA + OB$
Mặt khác theo công thức trung tuyến ta có: $O{I^2} = \dfrac{{O{A^2} + O{B^2}}}{2} - \dfrac{{A{B^2}}}{4} \Rightarrow O{A^2} + O{B^2} = 8.$
Theo BĐT Bunhiascopky ta có:$2\left( {O{A^2} + O{B^2}} \right) \ge {\left( {OA + OB} \right)^2} \Rightarrow OA + OB \le 4.$
Cho các số phức $w,\,\,z$ thỏa mãn \(\left| {w + i} \right| = \dfrac{{3\sqrt 5 }}{5}\) và \(5w = (2 + i)(z - 4).\) Giá trị lớn nhất của biểu thức \(P = \left| {z - 1 - 2i} \right| + \left| {z - 5 - 2i} \right|\) bằng
Ta có $5w = \left( {2 + i} \right)\left( {z - 4} \right) \Leftrightarrow 5w + 5i = \left( {2 + i} \right)z - 8 + i \Leftrightarrow 5\left| {w + i} \right| = \left| {\left( {2 + i} \right)z - 8 + i} \right|$
$ \Leftrightarrow \left| {\left( {2 + i} \right)z - 8 + i} \right| = 3\sqrt 5 \Leftrightarrow \left| {2 + i} \right|.\left| {z - \dfrac{{8 - i}}{{2 + i}}} \right| = 3\sqrt 5 \Leftrightarrow \left| {z - \dfrac{{8 - i}}{{2 + i}}} \right| = 3 \Leftrightarrow \left| {z - 3 + 2i} \right| = 3$
$ \Rightarrow $Tập hợp điểm $M\left( z \right)$ là đường tròn $\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 9,$ tâm $I\left( {3; - \,2} \right),\,\,R = 3.$
Gọi $A\left( {1;2} \right),\,\,B\left( {5;2} \right)$ và $E\left( {3;2} \right)$ là trung điểm của $AB$ suy ra $P = MA + MB$.
Lại có ${\left( {MA + MB} \right)^2} \le 2\left( {M{A^2} + M{B^2}} \right) = 4.M{E^2} + A{B^2}$$ \Rightarrow \,\,P$ lớn nhất $ \Leftrightarrow $$ME$ lớn nhất.
Mà $IE = 4 > R = 3$ Vậy ${P_{\max }} = \sqrt {4.M{E^2} + A{B^2}} = 2\sqrt {53} .$
