Cho hình chóp \(S.\,ABC\) có \(SA\) vuông góc với đáy. Tam giác \(ABC\) vuông cân tại \(B\), biết \(SA = AC = 2a\). Thể tích khối chóp \(S.ABC\) là
Do \(\Delta ABC\) vuông cân tại \(B\) có \(AC = 2a \Rightarrow AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = a\sqrt 2 \).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.\dfrac{1}{2}BA.BC = \dfrac{1}{6}.2a.a\sqrt 2 .a\sqrt 2 = \dfrac{{2{a^3}}}{3}\).
Cho hình lăng trụ \(ABC.\,A'B'C'\) có thể tích bằng \(V\). Gọi \(M\) là trung điểm cạnh \(BB'\), điểm \(N\) thuộc cạnh \(CC'\) sao cho \(CN = 2C'N\). Tính thể tích khối chóp \(A.\,BCNM\) theo \(V\).
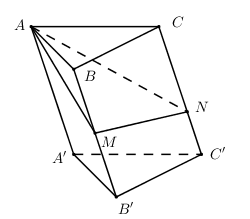
Ta có
\(\begin{array}{l}{S_{BCC'B'}} = d\left( {B;CC'} \right).CC'\\{S_{BMNC}} = \dfrac{{\left( {BM + CN} \right)d\left( {B;CC'} \right)}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}d\left( {B;CC'} \right)\left( {\dfrac{1}{2}CC' + \dfrac{2}{3}CC'} \right) = \dfrac{7}{{12}}d\left( {B;CC'} \right).CC'\end{array}\)
\( \Rightarrow \dfrac{{{S_{BMNC}}}}{{{S_{BCC'B'}}}} = \dfrac{7}{{12}} \).
Vì A.BMNC và A.BCC'B' có cùng chiều cao từ A nên
\( \dfrac{{{V_{A.BMNC}}}}{{{V_{A.BCC'B'}}}} =\dfrac{{\dfrac{1}{3}.d(A,(AMNC)).S_{AMNC}}}{\dfrac{1}{3}.d(A,(BCC'B')).S_{BCC'B'}}\)\(=\dfrac{{{S_{BMNC}}}}{{{S_{BCC'B'}}}}= \dfrac{7}{{12}} \Rightarrow {V_{A.BMNC}} = \dfrac{7}{{12}}{V_{A.BCC'B'}}\).
Có \(V_{A.A'B'C'}+V_{A.BCC'B'}=V\) và \(V_{A.A'B'C'}=\dfrac{1}{3}d(A,(A'B'C')).S_{A'B'C'}=\dfrac{1}{3}V\)
(Do \(d(A,(A'B'C')).S_{A'B'C'}=V\))
=> \({V_{A.BCC'B'}} = \dfrac{2}{3}V \Rightarrow {V_{A.BMNC}} = \dfrac{7}{{12}}.\dfrac{2}{3}V = \dfrac{7}{{18}}V\).
Cho khối chóp đều $S . A B C D$ có \(AB = 2a\) và thể tích bằng \(\dfrac{{4\sqrt 3 }}{3}{a^3}\). Côsin góc giữa hai mặt phẳng \((SAB)\) và \((SCD)\) bằng
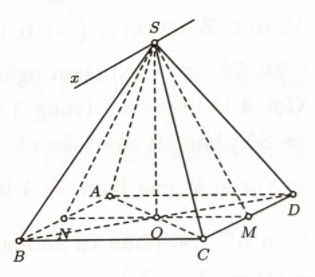
Bước 1: Gọi \(O\) là tâm hình vuông $A B C D$. Tính SO.
Gọi \(O\) là tâm hình vuông $A B C D$.
Ta có \({S_{ABCD}} = 4{a^2};{V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}} \cdot SO\) \( \Rightarrow SO = a\sqrt 3 \).
Mặt khác \(AB//CD\)\( \Rightarrow (SAB) \cap (SCD) = Sx//AB//CD.\)
Bước 2: Gọi $M, N$ lần lượt là trung điểm của $C D$ và $A B$.
Gọi $M, N$ lần lượt là trung điểm của $C D$ và $A B$. Ta có:
\(SN \bot AB \Rightarrow SN \bot Sx\)
\(SM \bot CD\)\( \Rightarrow SM \bot Sx\).
\( \Rightarrow ((SAB),(SCD)) = (SM,SN)\)\( = \widehat {MSN} = 2\widehat {MSO}.\)
Ta có
\(\tan \widehat {MSO} = \dfrac{{OM}}{{SO}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}\)\( \Rightarrow \widehat {MSO} = {30^0 } \Rightarrow \widehat {MSN} = {60^0}\)\( \Rightarrow \cos \widehat {MSN} = \dfrac{1}{2}\)
Cho hình chóp đều \(S.ABCD\) có cạnh \(AB = a\), góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^0\). Thể tích khối chóp \(S.\,ABCD\) là

Gọi \(O = AC \cap BD\) ta có \(SO \bot \left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;\left( {ABCD} \right)} \right) = \angle SAO = {45^0} \Rightarrow SO = OA = \dfrac{{a\sqrt 2 }}{2}\).
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\).
Cho hình chóp đều $S . A B C$ cạnh đáy bằng $2 a$ và cạnh bên bằng $3 a$. Gọi \(M\) là điểm thay đổi trên cạnh \(AB,(P)\) qua \(M\) và song song với $S A, B C$ chia khối chóp $S . A B C$ thành hai phần. Biết thiết diện của hình chóp $S . A B C$ cắt bởi \((P)\) là hình thoi. Tính thể tích phần chứa đỉnh \(A\).
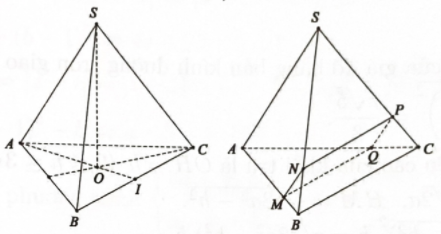
Bước 1: Gọi \(O\) là trọng tâm \(\Delta ABC,I\) là trung điểm $B C$. Chứng minh \(SO \bot (ABC)\)
Gọi \(O\) là trọng tâm \(\Delta ABC,I\) là trung điểm $B C$.
Gọi $N, P, Q$ lần lượt là giao điểm của \((P)\) với các cạnh $S B, S C, A C$.
$S A B C$ là hình chóp đều nên \(SO \bot (ABC)\).
Bước 2: Tính \({V_{SABC}} = \dfrac{1}{3}SO \cdot {S_{ABC}}\)
Tam giác ABC đều có cạnh bằng \(2a\).
\( \Rightarrow AO = \dfrac{2}{3}AI = \dfrac{2}{3} \cdot \dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}\)
Xét tam giác vuông $S O A$ có: \(SO = \sqrt {S{A^2} - A{O^2}} = \dfrac{{a\sqrt {69} }}{3}\).
Ta có: \({V_{SABC}} = \dfrac{1}{3}SO \cdot {S_{ABC}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt {69} }}{3} \cdot \dfrac{{{{(2a)}^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt {23} }}{3}\).
Bước 3: Tính MN theo a.
MNPQ là hình thoi \( \Rightarrow MN = MQ = x\).
Ta có: \(\dfrac{{MN}}{{SA}} + \dfrac{{MQ}}{{BC}} = 1 \Leftrightarrow \dfrac{x}{{3a}} + \dfrac{x}{{2a}} = 1\)\( \Leftrightarrow x = \dfrac{{6a}}{5}\).
Bước 4: Đặt \(\dfrac{{AM}}{{AB}} = t\). Tính \({V_{SAMNPQ}}\).
Đặt \(\dfrac{{AM}}{{AB}} = t\).
=> \(t = \dfrac{{AM}}{{AB}} = \dfrac{{MQ}}{{BC}} = \dfrac{{\dfrac{{6a}}{5}}}{{2a}} = \dfrac{3}{5}\).
Ta có công thức tính nhanh \(\dfrac{{{V_{SAMNPQ}}}}{{{V_{S.ABC}}}} = {t^2}(3 - 2t)\).
\( \Rightarrow \dfrac{{{V_{SAMNPQ}}}}{{{V_{S.ABC}}}} = {t^2}(3 - 2t) = \dfrac{{81}}{{125}}\)\( \Rightarrow {V_{SAMNPQ}} = \dfrac{{81}}{{125}}{V_{S.ABC}} = \dfrac{{27\sqrt {23} {a^3}}}{{125}}\)
Cho hình chóp đều \(S.ABC\), góc giữa mặt bên và mặt phẳng đáy \(\left( {ABC} \right)\) bằng \({60^0}\), khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng \(\dfrac{{3a}}{{2\sqrt 7 }}\). Thể tích của khối chóp \(S.ABC\) theo \(a\) bằng:
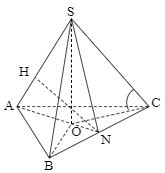
+ Gọi \(O\) là tâm tam giác đều \(ABC\) \( \Rightarrow SO \bot \left( {ABC} \right)\).
+ Gọi \(N\) là trung điểm \(BC\) ta có: \(\left\{ \begin{array}{l}BC \bot AN\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right) \Rightarrow BC \bot SN\).
+ \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SN \subset \left( {SBC} \right),\,\,SN \bot BC\\AN \subset \left( {ABC} \right),\,\,AN \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SN;AN} \right) = \angle SNA = {60^0}\).
+ Trong \(\left( {SAM} \right)\) kẻ \(NH \bot SA\,\,\left( {H \in SA} \right)\) \( \Rightarrow NH \bot BC\) \( \Rightarrow d\left( {SA;BC} \right) = NH = \dfrac{{3a}}{{2\sqrt 7 }}\).
+ Đặt \(ON = x \Rightarrow AN = 3x,\,\,OA = 2x\).
+ \(\Delta SON:\,\,SO = ON.\tan {60^0} = x\sqrt 3 \), \(SA = \sqrt {S{O^2} + O{A^2}} = \sqrt {3{x^2} + 4{x^2}} = x\sqrt 7 \).
+ \(\Delta SAN:\,\,{S_{\Delta SAN}} = \dfrac{1}{2}SO.AN = \dfrac{1}{2}NH.SA\)
\(\begin{array}{l} \Rightarrow SO.AN = NH.SA\\ \Rightarrow x\sqrt 3 .3x = \dfrac{{3a}}{{2\sqrt 7 }}.x\sqrt 7 \\ \Leftrightarrow x = \dfrac{a}{{2\sqrt 3 }}\end{array}\)
\(\begin{array}{l} \Rightarrow AM = 3a = \dfrac{{a\sqrt 3 }}{2} = \dfrac{{AB\sqrt 3 }}{2} \Rightarrow AB = a\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\end{array}\)
Và \(SO = x\sqrt 3 = \dfrac{a}{2}\).
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao bằng \(h\), góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng \(\alpha \). Tính thể tích của khối chóp \(S.ABCD\) theo \(h\) và \(\alpha \).
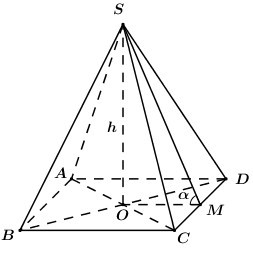
+ Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
+ Gọi \(M\) là trung điểm của \(CD\) ta có: \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\).
+ \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\SM \subset \left( {SCD} \right),\,\,SM \bot CD\\OM \subset \left( {ABCD} \right),\,\,OM \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = \alpha \).
+ \(\Delta SOM\): \(OM = SO.\cot \alpha = \dfrac{h}{{\tan \alpha }}\) \( \Rightarrow AD = 2OM = \dfrac{{2h}}{{\tan \alpha }}\) \( \Rightarrow {S_{ABCD}} = \dfrac{{4{h^2}}}{{{{\tan }^2}\alpha }}\).
+ \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.h.\dfrac{{4{h^2}}}{{{{\tan }^2}\alpha }} = \dfrac{{4{h^3}}}{{3{{\tan }^2}\alpha }}\).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại\(A\), \(SA\) vuông góc với đáy. Biết \(SA = BC = a\), thể tích khối chóp \(S.ABC\) bằng:
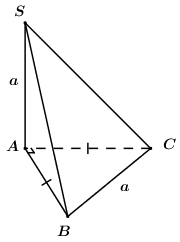
Ta có tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a\) \( \Rightarrow AB = AC = \dfrac{a}{{\sqrt 2 }}\).
Khi đó \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.\dfrac{a}{{\sqrt 2 }}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{{a^2}}}{4}\).
Vậy thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{4} = \dfrac{{{a^3}}}{{12}}.\)
Đề thi THPT QG - 2021 - mã 103
Cho khối chóp có diện tích đáy \(B = 7{a^2}\) và chiều cao \(h = a\). Thể tích của khối chóp đã cho bằng:
\({V_{chop}} = \dfrac{1}{3}{S_{day}} \times h = \dfrac{1}{3}B.h = \dfrac{1}{3}.7{a^2}.a = \dfrac{{7{a^3}}}{3}\).
Cho hình chóp \(S.ABCD\) đáy là hình chữ nhật, \(SA\) vuông góc với đáy, \(AB = a,\,\,AD = 2a.\) Góc giữa \(SB\) và đáy bằng \({45^0}.\) Thể tích khối chóp \(S.ABC\) bằng:
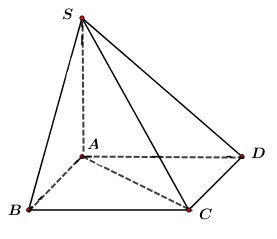
Ta có: \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow AB\) là hình chiếu của \(SB\) trên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,AB} \right) = \angle SBA = {45^0}\)
\( \Rightarrow \Delta SAB\) vuông cân tại \(A \Rightarrow SA = AB = a.\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}SA.\dfrac{1}{2}{S_{ABCD}}\) \( = \dfrac{1}{3}.a.\dfrac{1}{2}.a.2a = \dfrac{{2{a^3}}}{6}.\)
Cho hình chóp \(S.ABCD\) đáy là hình chữ nhật, \(SA\) vuông góc với đáy, \(AB = a,\,\,AD = 2a.\) Góc giữa \(SB\) và đáy bằng \({45^0}.\) Thể tích khối chóp \(S.ABC\) bằng:
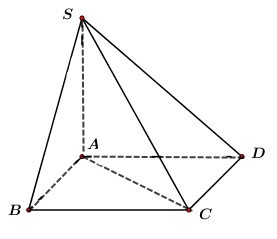
Ta có: \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow AB\) là hình chiếu của \(SB\) trên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,AB} \right) = \angle SBA = {45^0}\)
\( \Rightarrow \Delta SAB\) vuông cân tại \(A \Rightarrow SA = AB = a.\)
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}SA.\dfrac{1}{2}{S_{ABCD}}\) \( = \dfrac{1}{3}.a.\dfrac{1}{2}.a.2a = \dfrac{{2{a^3}}}{3}.\)
Cho khối chóp tứ giác đều có cạnh đáy bằng \(a,\) chiều cao bằng \(\dfrac{{a\sqrt 2 }}{2}.\) Thể tích khối chóp đã cho bằng:
Thể tích của khối chóp đã cho là:\(V = \dfrac{1}{3}Sh = \dfrac{1}{3}.{a^2}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A,\,\,AB = a,\) cạnh bên \(SC = 3a\) và \(SC\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABC\) bằng:
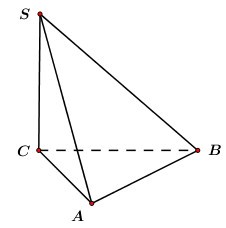
Ta có:\({S_{ABC}} = \dfrac{1}{2}A{B^2} = \dfrac{1}{2}{a^2}.\)
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SC.{S_{ABC}} = \dfrac{1}{3}.3a.\dfrac{1}{2}{a^2} \)\(= \dfrac{1}{2}{a^3}.\)
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\). Biết tam giác \(SBA\) vuông tại \(B\), tam giác \(SCA\) vuông tại \(C\) và khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng \(\dfrac{{3a}}{{\sqrt {13} }}\). Tính thể tích khối chóp \(S.ABC\).
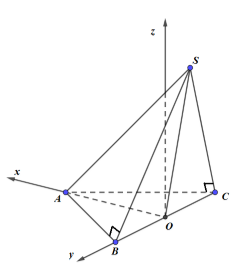
Gọi O là trung điểm của BC.
Ta gắn hệ trục tọa độ Oxyz như hình vẽ. Trong đó:
\(A\left( {\dfrac{{a\sqrt 3 }}{2};0;0} \right),\,B\left( {0;\dfrac{a}{2};0} \right),\,C\left( {0; - \dfrac{a}{2};0} \right)\)
Gọi \(\left( P \right)\) là mặt phẳng vuông góc với AB tại B, \(\left( Q \right)\) là mặt phẳng vuông góc với AC tại C. Gọi giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) là đường thẳng \(d\).
Do \(SB \bot AB,\,\,SC \bot AC\) nên \(S \in d\).
\(\overrightarrow {AB} = \left( { - \dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right),\,\,\overrightarrow {AC} = \left( { - \dfrac{{a\sqrt 3 }}{2}; - \dfrac{a}{2};0} \right)\)
Mặt phẳng \(\left( P \right)\) đi qua \(B\left( {0;\dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ; - 1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x - y + \dfrac{a}{2} = 0\).
Mặt phẳng \(\left( Q \right)\) đi qua \(C\left( {0; - \dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_2}} = \left( {\sqrt 3 ;1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x + y + \dfrac{a}{2} = 0\).
\(d\) là giao của \(\left( P \right)\) và \(\left( Q \right) \Rightarrow d:\left\{ \begin{array}{l}\sqrt 3 x - y + \dfrac{a}{2} = 0\\\sqrt 3 x + y + \dfrac{a}{2} = 0\end{array} \right.\), \(\left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {0;0;2\sqrt 3 } \right)\)
\( \Rightarrow d\) đi qua \(I\left( { - \dfrac{a}{{2\sqrt 3 }};0;0} \right)\)có 1 VTCP \(\overrightarrow u = \left( {0;0;1} \right)\), có phương trình tham số là: \(\left\{ \begin{array}{l}x = - \dfrac{a}{{2\sqrt 3 }}\\y = 0\\z = t\end{array} \right.\)
Giả sử \(S\left( { - \dfrac{a}{{2\sqrt 3 }};0;t} \right)\). Ta có: \(\begin{array}{l}\overrightarrow {SB} = \left( {\dfrac{a}{{2\sqrt 3 }};\dfrac{a}{2}; - t} \right);\,\,\\\overrightarrow {CA} = \left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right)\end{array}\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right] = \left( {\dfrac{{at}}{2};\dfrac{{a\sqrt 3 t}}{2}; - \dfrac{{{a^2}\sqrt 3 }}{6}} \right)\)\( \Rightarrow \left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right| = \sqrt {\dfrac{{{a^2}{t^2}}}{4} + \dfrac{{3{a^2}{t^2}}}{4} + \dfrac{{{a^2}}}{{12}}} = \sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} \)
Ta có: \(\overrightarrow {CB} = \left( {0;a;0} \right)\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} = 0 + \dfrac{{a\sqrt 3 t}}{2}.a + 0 = \dfrac{{{a^2}\sqrt 3 t}}{2}\)
\(d(SB;AC) = \dfrac{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} } \right|}}{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right|}} = \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }}\)
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }} = \dfrac{{3a}}{{\sqrt {13} }} \Leftrightarrow \dfrac{{3{a^4}{t^2}}}{{4{a^2}{t^2} + \dfrac{1}{3}{a^2}}} = \dfrac{{9{a^2}}}{{13}}\\ \Leftrightarrow 39{a^2}{t^2} = 36{a^2}{t^2} + 3{a^2} \Leftrightarrow {t^2} = {a^2} \Leftrightarrow t = a\end{array}\)
\( \Rightarrow S\left( { - \dfrac{a}{{2\sqrt 3 }};0;a} \right)\)\( \Rightarrow h = d\left( {S;\left( {Oxy} \right)} \right) = a\)
Diện tích tam giác đều ABC là: \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}.h.S = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
Cho khối chóp có chiều cao bằng 6, diện tích đáy bằng 4. Thể tích khối chóp đã cho bằng:
Thể tích khối chóp đã cho là: \(V = \dfrac{1}{3}Bh = \dfrac{1}{3}.6.4 = 8.\)
Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a.\) Cạnh bên \(SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(SABCD\) bằng:
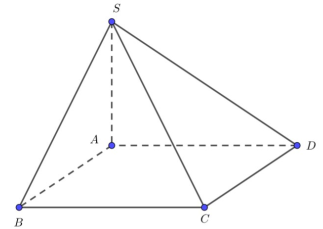
Thể tích khối chóp đã cho là: \({V_{SABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.3a.{a^2} = {a^3}.\)
Nếu khối chóp \(OABC\) thỏa mãn \(OA = a,\,\,OB = b,\,\,OC = c\) và \(OA \bot OB,\,\,OB \bot OC,\,\,OC \bot OA\) thì có thể tích là:
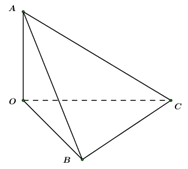
Thể tích khối đa diện \(OABC\) là: \({V_{OABC}} = \dfrac{1}{6}abc.\)
Cho hình chóp \(S.\,ABC\) có \(AB = AC = 4,\,BC = 2,\,SA = 4\sqrt 3 \), . Tính thể tích khối chóp \(S.\,ABC.\)
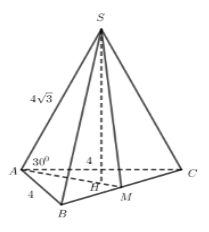
Dễ thấy \(\Delta SAB = \Delta SAC\left( {c.g.c} \right)\) nên \(SB = SC\) hay tam giác \(\Delta SBC\) cân.
Gọi \(M\) là trung điểm \(BC\) ta có: \(AM \bot BC,SM \bot BC \Rightarrow BC \bot \left( {SAM} \right)\).
Gọi \(H\) là hình chiếu của \(S\) trên \(AM\) thì \(SH \bot AM,SH \bot BC\) nên \(SH\) là đường cao của hình chóp.
Xét tam giác \(SAB\) có: \(S{B^2} = S{A^2} + A{B^2} - 2SA.AB\cos {30^0} = 16 \Rightarrow SB = 4 \Rightarrow SC = 4\).
Do đó \(S{M^2} = \dfrac{{S{B^2} + S{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow SM = \sqrt {15} \).
Tam giác \(ABC\) có \(A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow AM = \sqrt {15} \).
Khi đó \({S_{SAM}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 6\).
Do đó: \(SH = \dfrac{{2{S_{SAM}}}}{{AM}} = \dfrac{{2.6}}{{\sqrt {15} }} = \dfrac{{4\sqrt {15} }}{5}\).
\({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.\dfrac{1}{2}AM.BC.SH = \dfrac{1}{6}.\sqrt {15} .2.\dfrac{{4\sqrt {15} }}{5} = 4\).
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng \(60^\circ ,SA = 1,SB = 2,SC = 3\). Thể tích của khối chóp S.ABC bằng
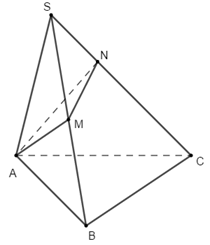
Ta lấy lần lượt trên cạnh SB; SC các điểm M;N sao cho \(SA = SM = SN = 1\)
Khi đó \(\frac{{{V_{SAMN}}}}{{{V_{SABC}}}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{AC}} = \frac{1}{2}.\frac{1}{3} = \frac{1}{6}\)
Tứ diện SAMN có góc ở đỉnh S là \(60^\circ \) và các cạnh bên bằng 1\( \Rightarrow SAMN\) là tứ diện đều.
Áp dụng công thức tính thể tích tứ diện đều là \(V = \frac{{\sqrt 2 }}{{12}}{a^3} = \frac{{\sqrt 2 }}{{12}}\)
Khi đó \({V_{SABC}} = \frac{{\sqrt 2 }}{2}\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(\angle ABC = {30^0}\). Tam giác \(SAB\) đều cạnh ‘\(a\) và hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm của cạnh \(AB\). Thể tích của khối chóp \(S.ABC\) là:
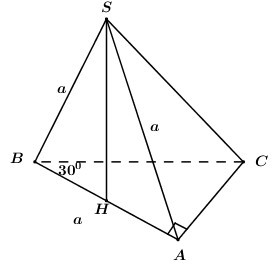
Gọi \(H\) là trung điểm của \(AB\) \( \Rightarrow SH \bot \left( {ABC} \right)\).
Tam giác \(SAB\) đều cạnh \(a\) \( \Rightarrow SH = \dfrac{{a\sqrt 3 }}{2}\).
Xét tam giác vuông \(ABC\): \(AC = AB.\tan {30^0} = \dfrac{{a\sqrt 3 }}{3}\) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.\dfrac{{a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 3 }}{6}\).
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{6} = \dfrac{{{a^3}}}{{12}}\).

