Mặt cầu

Ta thấy \(d\left( {I;\left( P \right)} \right) = \frac{R}{2} \Rightarrow r = \sqrt {{R^2} - d_{\left( {I;\left( p \right)} \right)}^2}  = \frac{{R\sqrt 3 }}{2}\).

Khi đó chu vi đường tròn bằng \(S = 2\pi r = R\sqrt 3 \pi \)

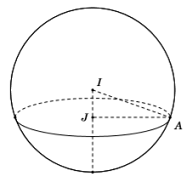
Gọi \(I,\,\,J\) theo thứ tự là tâm mặt cầu \(\left( S \right)\) và đường tròn \(\left( T \right)\), \(A\) là điểm bất kì thuộc đường tròn \(\left( T \right)\). Khi đó ta có \(IJ = 3\), \(2\pi .AJ = 12\pi  \Leftrightarrow AJ = 6\).

Áp dụng định lí Pytago trong tam giác vuông \(AIJ\) ta có: \(AI = \sqrt {A{J^2} + I{J^2}}  = \sqrt {{6^2} + {3^2}}  = 3\sqrt 5 \).

\( \Rightarrow \) Bán kính của mặt cầu  là \(R = 3\sqrt 5 \).

Vậy diện tích mặt cầu \(\left( S \right)\) là: \(S = 4\pi {R^2} = 4\pi .{\left( {3\sqrt 5 } \right)^2} = 180\pi .\)

Điểm \(M\) thuộc mặt cầu tâm \(O\) bán kính \(R\) nếu \(OM = R\).

Điểm \(M\) thuộc khối cầu tâm \(O\) bán kính \(R\) nếu \(OM \le R\).

Điểm \(M\) thuộc mặt cầu tâm \(O\) bán kính \(R\) thì \(OM = R\).

Điểm \(M\) thuộc khối cầu tâm \(O\) bán kính \(R\) thì \(OM \le R\).

Do đó điểm thuộc mặt cầu sẽ thuộc khối cầu.

Điểm không thuộc mặt cầu thì có thể nằm ngoài hoặc nằm trong mặt cầu nên các điểm nằm trong mặt cầu vẫn thuộc khối cầu.

Do đó \(C\) sai.

Nếu \(OH < R\) thì \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là một đường tròn.

Nếu mặt phẳng cắt mặt cầu tại nhiều hơn \(1\) điểm thì giao tuyến của chúng là một đường tròn nằm trên mặt cầu.

Nếu \(\left( P \right)\) là mặt phẳng kính thì \(OH = 0\left( {H \equiv O} \right)\) hay \(\left( P \right)\) đi qua \(O\) là tâm mặt cầu.

Nếu \(\left( P \right)\) là mặt phẳng kính thì \(OH = 0\left( {H \equiv O} \right)\) hay \(\left( P \right)\) đi qua \(O\) là tâm mặt cầu, do đó \(\left( P \right)\) đi qua đường kính của mặt cầu.

Mọi mặt phẳng đi qua tâm mặt cầu đều là mặt phẳng kính của mặt cầu.

Do đó có vô số mặt phẳng đi qua tâm thì sẽ có vô số mặt phẳng kính.

- Mọi đường tròn lớn của một mặt cầu đều có tâm là tâm mặt cầu nên A đúng.

- Mọi mặt phẳng kính của mặt cầu đều cùng đi qua một điểm (đó là tâm mặt cầu) chứ không phải cùng một đường kính mặt cầu nên B và D đều sai.

- Mọi đường tròn lớn của một mặt cầu đều có bán kính bằng bán kính mặt cầu nên C sai.

Mặt cầu \(\left( S \right)\) và đường thẳng \(d\) không có điểm chung nếu \(d\left( {O;d} \right) > R\).

Đường thẳng và mặt cầu chỉ có thể có số giao điểm là \(0;1;2\) nên số giao điểm lớn nhất có thể có là \(2\) giao điểm.

Qua một điểm nằm trong mặt cầu ta không vẽ được tiếp tuyến nào.

Qua một điểm nằm trên mặt cầu ta vẽ được duy nhất \(1\) mặt phẳng tiếp diện với mặt cầu tại điểm đó.

Các tiếp tuyến của mặt cầu tại cùng một điểm thì cùng thuộc mặt phẳng tiếp diện của mặt cầu tại điểm đó.

Đáp án A: Mọi đường thẳng đi qua \(A\) và nằm trong \(\left( P \right)\) đều là tiếp tuyến của \(\left( S \right)\) (đúng).

Đáp án B: Mọi đường thẳng nằm trong \(\left( P \right)\) đều tiếp xúc với \(\left( S \right)\) (sai vì chỉ những đường thẳng đi qua \(A\) và nằm trong \(\left( P \right)\) mới tiếp xúc với \(\left( S \right)\))

Đáp án C: Các đường thẳng nằm trong \(\left( P \right)\) không thể có với \(\left( S \right)\) hai điểm chung (đúng, chỉ có thể không có hoặc có duy nhất một điểm chúng).

Đáp án D: Đường thẳng \(OA\) vuông góc với \(\left( P \right)\) tại \(A\) (đúng vì \(A\) là tiếp điểm).

Qua một điểm nằm ngoài mặt cầu vẽ được vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm với mặt cầu là đường tròn nằm trên mặt cầu.

Do đó bốn điểm \(B,C,D,E\) cùng thuộc một đường tròn.

+ Nếu điểm \(A\) nằm trong mặt cầu thì không vẽ được tiếp tuyến nên loại đáp án D.

+ Nếu điểm \(A\) nằm trên mặt cầu thì vẽ được các tiếp tuyến thuộc mặt phẳng tiếp diện nên (hay nó chỉ tiếp xúc với mặt cầu) loại đáp án A.

+ Nếu điểm \(A\) nằm ngoài mặt cầu thì vẽ được vô số tiếp tuyến với mặt cầu đi qua \(A\) nhưng các tiếp tuyến đều đồng quy tại \(A\).

Trong khi đó, tiếp tuyến với mặt cầu tại các điểm thuộc đường tròn lớn thì song song với nhau nên không có trường hợp nào thỏa mãn.