Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {3; - 2;3} \right)\) và $B\left( { - 1;2;5} \right)$. Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).
Tọa độ trung điểm \(I\) của đoạn \(AB\) với \(A(3; - 2;3)\) và \(B( - 1;2;5)\) được tính bởi
\(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2} = 1\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2} = 0\\{z_I} = \dfrac{{{z_A} + {z_B}}}{2} = 4\end{array} \right. \Rightarrow I\left( {1;\,0;4} \right)\)
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm \(M\left( {a;\,\,b;\,\,c} \right)\). Mệnh đề nào sau đây là sai?
Ta có: \(d\left( {M,\left( {Oxy} \right)} \right) = |c|\), nên mệnh đề B sai.
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1\\y = 2 + 3t\\z = 5 - t\end{array} \right.\,\,\left( {t \in \mathbb{R}} \right)\). Vectơ nào dưới đây là vectơ chỉ phương của $d$ ?
Đường thẳng \(d:\left\{ \begin{array}{l}x = 1\\y = 2 + 3t\\z = 5 - t\end{array} \right.\;\;(t \in \mathbb{R})\) nhận véc tơ \(\overrightarrow u = (0;3; - 1)\) làm VTCP.
Trong không gian với hệ tọa độ $Oxyz,$ cho hai điểm $A\left( { - 2;3;1} \right)$và $B\left( {5;{\rm{ }}6;{\rm{ }}2} \right)$. Đường thẳng $AB$cắt mặt phẳng $\left( {Oxz} \right)$ tại điểm $M$. Tính tỉ số $\dfrac{{AM}}{{BM}}$.
\(M \in \left( {Oxz} \right){\rm{ }} \Rightarrow M\left( {x{\rm{ ; 0 ; }}z} \right)\)
\(\overrightarrow {AB} = \left( {7{\rm{ ; }}3{\rm{ ; }}1} \right){\rm{ }} \Rightarrow AB = \sqrt[{}]{{59}}\)
\(\overrightarrow {AM} = \left( {x + 2{\rm{ ;}} - 3{\rm{ ; }}z - 1} \right)\)và
\(A,B,M\)thẳng hàng \( \Rightarrow \overrightarrow {AM} = k.\overrightarrow {AB} {\rm{ }}\left( {k \in \mathbb{R}} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}x + 2 = 7k\\ - 3 = 3k\\z - 1 = k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 9\\ - 1 = k\\z = 0\end{array} \right.\)\( \Rightarrow M\left( { - 9{\rm{ ; 0 ; }}0} \right)\)
\(\overrightarrow {BM} = \left( { - 14{\rm{ ;}} - 6{\rm{ ;}} - 2} \right) \Rightarrow BM = \sqrt[{}]{{236}} = 2\sqrt {59} \)
\(\overrightarrow {AM} = \left( { - 7; - 3; - 1} \right) \Rightarrow AM = \sqrt {59} \)
\( \Rightarrow \dfrac{{AM}}{{BM}} = \dfrac{1}{2}\).
Trong không gian với hệ trục $Oxyz$, mặt phẳng đi qua điểm \(A\left( {1;3; - 2} \right)\) và song song với mặt phẳng \(\left( P \right):2x - y + 3z + 4 = 0\) là
Mặt phẳng \(\left( Q \right)\) song song với mặt phẳng \(\left( P \right):2x - y + 3z + 4 = 0\) có dạng:
\(\left( Q \right):2x - y + 3z + D = 0,{\rm{ }}\left( {D \ne 4} \right)\)
Mặt phẳng \(\left( Q \right)\) đi qua điểm \(A\left( {1;3; - 2} \right)\) ta có: \(2.1 - 3 + 3.\left( { - 2} \right) + D = 0 \Leftrightarrow D = 7 \ne 4\)(thỏa mãn)
Vậy phương trình mặt phẳng \(\left( Q \right):2x - y + 3z + 7 = 0\).
Trong không gian với hệ tọa độ \(Oxyz\), đường thẳng \(\Delta :\dfrac{x}{1} = \dfrac{y}{1} = \dfrac{z}{2}\) vuông góc với mặt phẳng nào trong các mặt phẳng sau?
\(\Delta \bot \left( P \right) \Rightarrow \)\({\vec u_\Delta }\)cùng phương với \({\vec n_{\left( P \right)}}\).
Ta có VTCP của \(\Delta :\overrightarrow {{u_\Delta }} = \left( {1,1,2} \right)\), VTPT của \(\left( \alpha \right)\): \({\vec n_{\left( \alpha \right)}} = \left( {1;1;2} \right)\).
Suy ra \({\vec u_\Delta }\)cùng phương với \({\vec n_{\left( \alpha \right)}}\).
Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A\left( {1; - 2; - 1} \right)$, $B\left( {1;0;2} \right)$ và $C\left( {0;2;1} \right)$. Viết phương trình mặt phẳng qua $A$ và vuông góc với đường thẳng $BC$
Ta có $\overrightarrow {BC} = \left( { - 1;2; - 1} \right)$ là vectơ pháp tuyến của mặt phẳng, đồng thời mặt phẳng đi qua $A\left( {1; - 2; - 1} \right)$ nên mặt phẳng cần tìm là: $ - \left( {x - 1} \right) + 2\left( {y + 2} \right) - \left( {z + 1} \right) = 0$$ \Leftrightarrow x - 2y + z - 4 = 0$.
Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng $\left( P \right)$ qua điểm \(A\left( {1;\; - 3;\;2} \right)\) và vuông góc với hai mặt phẳng \(\left( \alpha \right):x + 3 = 0\), \(\left( \beta \right):z - 2 = 0\) có phương trình là
$\left( P \right)$ có véctơ pháp tuyến là $\overrightarrow {{n_{\left( P \right)}}} = \left[ {\overrightarrow {{n_{\left( \alpha \right)}}} ,\overrightarrow {{n_{\left( \beta \right)}}} } \right] = \left( {0;\; - 1;\;0} \right)$ và qua \(A\left( {1;\; - 3\;2} \right)\)\( \Rightarrow \left( P \right):y + 3 = 0\)
Trong không gian với hệ tọa độ ${\rm{Ox}}yz$, gọi $M,\,\,N,\,\,P$ lần lượt là hình chiếu vuông góc của \(A\left( {2;\,\, - 1;\,\,1} \right)\) lên các trục $Ox,\,\,Oy,\,\,Oz$. Mặt phẳng đi qua\(A\) và song song với mặt phẳng \(\left( {MNP} \right)\) có phương trình là
Ta có: \(M\left( {2;\,\,0;\,\,0} \right),\,\,N\left( {0;\,\, - 1;\,\,0} \right),\,\,P\left( {0;\,\,0;\,\,1} \right)\)
\( \Rightarrow \left( {MNP} \right):\dfrac{x}{2} - \dfrac{y}{1} + \dfrac{z}{1} = 1 \Leftrightarrow x - 2y + 2z - 2 = 0\)
Mặt phẳng đi qua \(A\) và song song với mặt phẳng \(\left( {MNP} \right)\) có phương trình là: \(x - 2y + 2z - 6 = 0\).
Trong không gian với hệ tọa độ \(Oxyz\), gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng \(\Delta \) có phương trình \(\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{2}\) và vuông góc với mặt phẳng \(\left( \beta \right):x + y - 2z - 1 = 0\). Giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) đi qua điểm nào trong các điểm sau
Ta có véctơ chỉ phương của đường thẳng \(\Delta \) là \(\overrightarrow u \left( {1;1;2} \right)\)
Véctơ pháp tuyến của mặt phẳng \(\left( \beta \right):x + y - 2z - 1 = 0\) là \(\overrightarrow n \left( {1;1; - 2} \right)\).
Vì \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng \(\Delta \) có phương trình \(\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{2}\) và vuông góc với mặt phẳng \(\left( \beta \right):x + y - 2z - 1 = 0\) nên \(\left( \alpha \right)\) có một véctơ pháp tuyến là \(\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow u ,\overrightarrow n } \right] = \left( { - 4;4;0} \right) = 4\left( {1; - 1;0} \right) = 4.\overrightarrow a \)
Gọi \(d = \left( \alpha \right) \cap \left( \beta \right)\), suy ra \(d\) có véctơ chỉ phương là \(\overrightarrow {{u_d}} = \left[ {\overrightarrow a ,\overrightarrow n } \right] = \left( {2;2;2} \right) = 2\left( {1;1;1} \right)\).
Giao điểm của đường thẳng \(\Delta \) có phương trình \(\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{1} = \dfrac{z}{2}\) và mặt phẳng \(\left( \beta \right):x + y - 2z - 1 = 0\)là \(I\left( {3;2;2} \right)\).
Suy ra phương trình đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 3 + t}\\{y = 2 + t}\\{z = 2 + t}\end{array}} \right.\).
Vậy \(A\left( {2;1;1} \right)\) thuộc đường thẳng \(d\).
Trong không gian với hệ tọa độ $Oxyz,$ viết phương trình mặt phẳng \(\left( P \right)\) song song và cách đều hai đường thẳng \({d_1}:\dfrac{{x - 2}}{{ - 1}} = \dfrac{y}{1} = \dfrac{z}{1}\) và \({d_2}:\dfrac{x}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{{z - 2}}{{ - 1}}\)
Ta có:
\({d_1}\) đi qua điểm \(A\left( {2;0;0} \right)\) và có VTCP \({\vec u_1} = \left( { - 1;1;1} \right)\).
\({d_2}\) đi qua điểm \(B\left( {0;1;2} \right)\) và có VTCP \({\vec u_2} = \left( {2; - 1; - 1} \right)\)
Vì \(\left( P \right)\) song song với hai đường thẳng \({d_1}\) và \({d_2}\) nên VTPT của \(\left( P \right)\) là \(\vec n = \left[ {{{\vec u}_1},{{\vec u}_2}} \right] = \left( {0;1; - 1} \right)\)
Khi đó \(\left( P \right)\) có dạng \(y - z + D = 0\)
\( \Rightarrow \)loại đáp án A và C.
Lại có \(\left( P \right)\) cách đều \({d_1}\) và \({d_2}\) nên \(\left( P \right)\) đi qua trung điểm \(M\left( {0;\dfrac{1}{2};1} \right)\) của \(AB\)
Do đó \(\left( P \right):2y - 2z + 1 = 0\)
Trong không gian với hệ tọa độ ${\rm{Ox}}yz$, mặt phẳng \(\left( \alpha \right)\) chắn các trục $Ox,\,\,Oy,\,\,Oz$ lần lượt tại $A,\,\,B,\,\,C$ sao cho $H\left( {3;\,\, - 4;\,\,2} \right)$ là trực tâm của tam giác \(ABC\). Phương trình mặt phẳng \(\left( \alpha \right)\) là
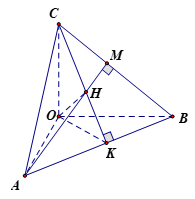
Gọi \(CK,\,\,AM\) là hai đường cao của tam giác \(ABC\).
Suy ra \(H = AM \cap CK\).
Ta có: $\left. \begin{array}{l}AB \bot \left( {OKC} \right) \Rightarrow AB \bot OH\\BC \bot \left( {AOM} \right) \Rightarrow BC \bot OH\end{array} \right\} \Rightarrow OH \bot \left( {ABC} \right)$
Mặt phẳng $\left( {ABC} \right)$đi qua điểm $H$ và nhận \(\overrightarrow {OH} \) làm một \(VTPT\)
Nên mặt phẳng $\left( {ABC} \right)$ có phương trình: \(3x - 4y + 2z - 29 = 0\).
Trong không gian với hệ tọa độ ${\rm{Ox}}yz$, cho ba điểm \(A\left( {2; - 1;0} \right),B\left( { - 1;2; - 2} \right)\) và \(C\left( {3;0; - 4} \right)\). Viết phương trình đường trung tuyến đỉnh \(A\) của tam giác \(ABC\).
Gọi \(M\left( {1;1; - 3} \right)\) là trung điểm của cạnh \(BC\), ta có \(\overrightarrow {AM} = \left( { - 1;2; - 3} \right) = - 1.\left( {1; - 2;3} \right)\) là VTCP của đường thẳng nên \(AM:\dfrac{{x - 2}}{1} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{z}{3}\)
Trong không gian với hệ tọa độ $Oxyz$, gọi \(\Delta \) là giao tuyến của hai mặt phẳng \(x - y + 3z - 1 = 0\) và \(3x - 7z + 2 = 0\). Một vectơ chỉ phương của \(\Delta \) là
Hai mặt phẳng đã cho có VTPT lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1;3} \right),\overrightarrow {{n_2}} = \left( {3;0; - 7} \right)\)
\(\Delta \) có VTCP là \(\overrightarrow u = \left[ {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right] = \left( {7;16;3} \right)\)
Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(M\left( {3;3; - 2} \right)\) và hai đường thẳng \({d_1}:\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{3} = \dfrac{z}{1}\); \({d_2}:\dfrac{{x + 1}}{{ - 1}} = \dfrac{{y - 1}}{2} = \dfrac{{z - 2}}{4}\). Đường thẳng \(d\) qua \(M\) cắt \({d_1},{d_2}\) lần lượt \(A\) và \(B\). Tính độ dài đoạn thẳng \(AB\).
Ta có \(A \in {d_1} \Rightarrow A\left( {1 + a;2 + 3a;a} \right),\)\(B \in {d_2} \Rightarrow B\left( { - 1 - b;1 + 2b;2 + 4b} \right)\)
\(\overrightarrow {MA} = \left( {a - 2;3a - 1;a + 2} \right),\overrightarrow {MB} = \left( { - b - 4;2b - 2;4b + 4} \right)\)
Ta có \(A,B,M\)thẳng hàng nên: \(\overrightarrow {MA} = k\overrightarrow {MB} \;\left( {k \in \mathbb{R}} \right) \Leftrightarrow \left\{ \begin{array}{l}a - 2 = k\left( { - b - 4} \right)\\3a - 1 = k\left( {2b - 2} \right)\\a + 2 = k\left( {4b + 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5ab + 10a - 5b = 0\\5ab + 7a - 4b = 0\\a + 2 = k\left( {4b + 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 0\\a = \dfrac{{10}}{9}\end{array} \right.\\a + 2 = k\left( {4b + 4} \right)\end{array} \right.\)
Với $a = 0 \Rightarrow b = 0 \Rightarrow A\left( {1;2;0} \right),B\left( { - 1;1;2} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = 3$
Với \(a = \dfrac{{10}}{9} \Rightarrow b = 20 \Rightarrow A\left( {\dfrac{{19}}{9};\dfrac{{16}}{3};\dfrac{{10}}{9}} \right),B\left( { - 21;41;32} \right)\)
Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới dây là phương trình mặt cầu có tâm $I\left( {1;2; - 1} \right)$ và tiếp xúc với mặt phẳng $\left( P \right):x - 2y - 2z - 8 = 0$?
Gọi mặt cầu cần tìm là $(S)$.
Ta có $(S)$ là mặt cầu có tâm $I(1;2; - 1)$ và bán kính $R$.
Vì $(S)$ tiếp xúc với mặt phẳng $(P):x - 2y - 2z - 8 = 0$ nên ta có
$R = d(I;(P)) = \dfrac{{\left| {1 - 2.2 - 2.( - 1) - 8} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {{( - 2)}^2}} }} = 3$.
Vậy phương trình mặt cầu cần tìm là ${\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9$.
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right)\) có tâm \(I\) thuộc đường thẳng \(\Delta :\dfrac{x}{1} = \dfrac{{y + 3}}{1} = \dfrac{z}{2}\). Biết rằng mặt cầu \(\left( S \right)\) có bán kính bằng \(2\sqrt 2 \) và cắt mặt phẳng $\left( {Oxz} \right)$ theo một đường tròn có bán kính bằng \(2\). Tìm tọa độ của điểm \(I\).
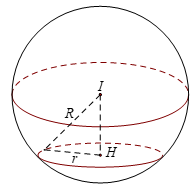
Mặt phẳng \(\left( {Oxz} \right):y = 0\). \(I \in \Delta :\dfrac{x}{1} = \dfrac{{y + 3}}{1} = \dfrac{z}{2} \Rightarrow I\left( {t; - 3 + t;2t} \right)\)
Gọi $H$ là hình chiếu của \(I\) lên mặt phẳng \(\left( {Oxz} \right)\). \(R,{\rm{ }}r\)lần lượt là bán kính mặt cầu và bán kính đường tròn giao tuyến. Theo bài ta có \(IH = d\left( {I,\left( {Oxz} \right)} \right) = \sqrt {{R^2} - {r^2}} = \sqrt {8 - 4} = 2\)
\( \Leftrightarrow \dfrac{{\left| { - 3 + t} \right|}}{1} = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = 5}\end{array}} \right.\) .
Với \(t = 1 \Rightarrow I\left( {1; - 2;2} \right)\) , với \(t = 5 \Rightarrow I\left( {5;2;10} \right)\).
Trong không gian với hệ tọa độ $Oxyz$ cho ba mặt phẳng \(\left( P \right):\,3x + y + z - 4 = 0,\,\left( Q \right):\,3x + y + z + 5 = 0\)và \(\left( R \right):\,2x - 3y - 3z + 1 = 0\). Xét các mệnh đề (1): \(\left( P \right)\parallel \left( Q \right)\)và (2): \(\left( P \right) \bot \left( R \right)\). Khẳng định nào sau đây đúng?
Do \(\overrightarrow {{n_P}} = \overrightarrow {{n_Q}} \) và \(M\left( {0;0;4} \right) \in \left( P \right)\) nhưng không thuộc \(\left( Q \right)\) nên \(\left( P \right)\parallel \left( Q \right)\)vậy (1) đúng.
Mặt khác \(\overrightarrow {{n_P}} .\overrightarrow {{n_R}} = 0\) nên \(\left( P \right) \bot \left( R \right)\) nên (2) đúng.
Vậy (1) và (2) đúng.
Trong không gian với hệ tọa độ $Oxyz$, tìm tất cả các giá trị thực của $m$ để đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{{ - 1}} = \dfrac{{z + 1}}{1}\) song song với mặt phẳng $\left( P \right):x + y - z + m = 0$.
Ta có: \(\overrightarrow u \left( {2; - 1;1} \right)\) là vectơ chỉ phương của \(\Delta \), \(\overrightarrow n \left( {1;1; - 1} \right)\) là vectơ pháp tuyến của $\left( P \right)$, \(M\left( {1; - 2; - 1} \right) \in \Delta \) .
\(\Delta {\rm{//}}\left( P \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u \bot \overrightarrow n \\M \notin \left( P \right)\end{array} \right.\)\( \Rightarrow \)$m \ne 0$.
Trong không gian với hệ trục $Oxyz$, cho đường thẳng \(d:\,x - 1 = \dfrac{{y - 2}}{2} = \dfrac{{z - 4}}{3}\) và mặt phẳng \(\left( P \right):\,x + 4y + 9z - 9 = 0\). Giao điểm \(I\) của \(d\) và \(\left( P \right)\) là
Ta có: \(d:\,x - 1 = \dfrac{{y - 2}}{2} = \dfrac{{z - 4}}{3} \Leftrightarrow d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = 4 + 3t\end{array} \right.\).
Tọa độ giao điểm của \(d\)và \(\left( P \right)\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = 4 + 3t\\x + 4y + 9z - 9 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 1\\x = 0\\y = 0\\z = 1\end{array} \right.\).
Suy ra: \(d \cap \left( P \right) = I\left( {0;\,0;\,1} \right)\)

