Biết \({x_1}\), \({x_2}\) \(\left( {{x_1} < {x_2}} \right)\) là hai nghiệm của phương trình \({\log _3}\left( {\sqrt[{}]{{{x^2} - 3x + 2}} + 2} \right) + {5^{{x^2} - 3x + 1}} = 2\) và \({x_1} + 2{x_2} = \dfrac{1}{2}\left( {a + \sqrt[{}]{b}} \right)\) với \(a\), \(b\) là hai số nguyên dương. Tính \(a - b\).
Điều kiện \(x \in \left( { - \infty \,;\,1} \right] \cup \left[ {2\,;\, + \infty } \right)\).
Đặt \(\sqrt[{}]{{{x^2} - 3x + 2}} = t\) với \(t \ge 0\).
Ta có \({x^2} - 3x + 1 = {t^2} - 1\).
Phương trình đã cho trở thành \({\log _3}\left( {t + 2} \right) + {5^{{t^2} - 1}} = 2\) \(\left( * \right)\)
Xét hàm số \(f\left( t \right) = {\log _3}\left( {t + 2} \right) + {5^{{t^2} - 1}}\) trên \(\left[ {0\,;\, + \infty } \right)\)
Có \(f'\left( t \right) = \dfrac{1}{{\left( {t + 2} \right)\ln 3}} + {5^{{t^2} - 1}}.2t\ln 5 > 0\) với \(t \ge 0\)
Do đó hàm số đồng biến trên \(\left[ {0\,;\, + \infty } \right)\).
Mặt khác \(f\left( 1 \right) = 2\). Phương trình \(\left( * \right)\) có dạng: \(f\left( t \right) = f\left( 1 \right)\) \( \Rightarrow t = 1\).
Với \(t = 1 \Rightarrow \sqrt[{}]{{{x^2} - 3x + 2}} = 1\)\( \Leftrightarrow {x^2} - 3x + 2 = 1\) \( \Rightarrow {x_1} = \dfrac{{3 - \sqrt[{}]{5}}}{2}\), \({x_2} = \dfrac{{3 + \sqrt[{}]{5}}}{2}\) (vì $x_1<x_2$)
Vậy \({x_1} + 2{x_2} = \dfrac{1}{2}\left( {9 + \sqrt[{}]{5}} \right)\) \( \Rightarrow \left\{ \begin{array}{l}a = 9\\b = 5\end{array} \right.\) \( \Rightarrow a - b = 4\)
Biết rằng \({2^{x + \dfrac{1}{x}}} = {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right]\) trong đó \(x > 0.\)
Tính giá trị của biểu thức \(P = {x^2} + {y^2} - xy + 1.\)
Áp dụng bất đẳng thức Cauchy ta có \(x + \dfrac{1}{x} \ge 2 \Rightarrow {2^{x + \dfrac{1}{x}}} \ge 4\).
Lại có \(14 - \left( {y - 2} \right)\sqrt {y + 1} = 14 - \left( {y + 1} \right)\sqrt {y + 1} + 3\sqrt {y + 1} \)
Đặt \(t = \sqrt {y + 1} \ge 0.\) Xét hàm số \(f\left( t \right) = - {t^3} + 3t + 14\) trên \(\left[ {0;\; + \infty } \right)\), ta có
\(f'\left( t \right) = - 3{t^2} + 3\). Do đó \(f'\left( t \right) = 0 \Leftrightarrow - 3{t^2} + 3 = 0 \Leftrightarrow t = 1\) vì \(t \in \left[ {0;\; + \infty } \right)\).
Từ đó ta có \(\mathop {\max }\limits_{\left[ {0;\; + \infty } \right)} f\left( t \right) = f\left( 1 \right) = 16.\)
Vậy \(14 - \left( {y - 2} \right)\sqrt {y + 1} \le 16\) \( \Rightarrow {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right] \le 4\)
Khi đó
\({2^{x + \dfrac{1}{x}}} = {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right] \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 0.\end{array} \right.\) \( \Rightarrow P = 2.\)
Cho \(x\), \(y\) là các số thực thỏa \({\log _{3x + y}}\left( {{x^2} + {y^2}} \right) \le 1\). Khi \(3x + y\) đạt giá trị lớn nhất, thì giá trị \(k = \dfrac{x}{y}\) là
Điều kiện: $0<3x+y \ne 1$
Do giả thiết \(3x + y\) đạt giá trị lớn nhất nên ta chỉ cần xét trường hợp \(3x + y > 1\)
\({\log _{3x + y}}\left( {{x^2} + {y^2}} \right) \le 1 \Leftrightarrow {x^2} + {y^2} \le 3x + y\,\,\)\(\left( 1 \right)\)
Đặt \(P = 3x + y \Rightarrow y = P - 3x\).
\(\left( 1 \right) \Leftrightarrow {x^2} + {\left( {P - 3x} \right)^2} - P \le 0\)\( \Leftrightarrow 10{x^2} - 6Px + {P^2} - P \le 0\)\(\left( 2 \right)\)
\(\Delta ' = 9{P^2} - 10\left( {{P^2} - P} \right) = - {P^2} + 10P\)
Nếu \(\Delta ' < 0\) thì \(\left( 2 \right)\) vô nghiệm.
Do đó \(\Delta ' \ge 0 \Leftrightarrow 0 \le P \le 10\).
Vậy \({P_{\max }} = 10\). Khi đó \(\left( 2 \right) \Leftrightarrow x = \dfrac{{3P}}{{10}} = 3 \Rightarrow y = 1 \Rightarrow k = \dfrac{x}{y} = 3\)
Gọi $S$ là tập nghiệm của phương trình $\left( {2 - x} \right)\left( {2 + {4^x}} \right) = 6$. Khi đó số phần tử của tập $S$ là bao nhiêu
Ta có:
$\left( {2 - x} \right)\left( {2 + {4^x}} \right) = 6 \Leftrightarrow \left( {2 - x} \right)\left( {2 + {4^x}} \right) - 6 = 0$
Xét hàm số $f\left( x \right) = \left( {2 - x} \right)\left( {2 + {4^x}} \right) - 6$ có tập xác định $D = \mathbb{R}$.
Dễ thấy $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm trên $\mathbb{R}$.
Theo định lý Rolle:
+ Trên đoạn $\left[ {0;\dfrac{1}{2}} \right]$ ta có $f\left( 0 \right) = f\left( {\dfrac{1}{2}} \right) = 0$ nên $\exists {c_1} \in \left( {0;\dfrac{1}{2}} \right)$: $f'\left( {{c_1}} \right) = 0$.
+ Trên đoạn $\left[ {\dfrac{1}{2};1} \right]$ ta có $f\left( 1 \right) = f\left( {\dfrac{1}{2}} \right) = 0$ nên $\exists {c_2} \in \left( {\dfrac{1}{2};1} \right)$: $f'\left( {{c_2}} \right) = 0$.
Do đó $f'\left( x \right) = 0$ có ít nhất hai nghiệm phân biệt ${c_1}$, ${c_2}$.
Mặt khác ta xét $f'\left( x \right) = - \left( {2 + {4^x}} \right) + {4^x}\ln 4\left( {2 - x} \right)$,
$f''\left( x \right) = - {4^x}\ln 4 + {4^x}{\ln ^2}4\left( {2 - x} \right) - {4^x}\ln 4$$ = {4^x}\left( { - 2\ln 4 + 2{{\ln }^2}4 - x{{\ln }^2}4} \right) = 0$
$ \Rightarrow x = \dfrac{{2 - 2\ln 4}}{{\ln 4}}$.
Vậy $f''\left( x \right) = 0$ có nghiệm duy nhất suy ra $f'\left( x \right) = 0$ có nhiều nhất hai nghiệm.
Mà ta đã chứng minh được $f'(x)$ có ít nhất $2$ nghiệm ở trên nên $f'(x)=0$ chỉ có $2$ nghiệm.
Suy ra $f\left( x \right) = 0$ có nhiều nhất là ba nghiệm.
Ngoài ra, $3$ nghiệm đó là: $0;\dfrac{1}{2};1$ nên phương trình đã cho chỉ có \(3\) nghiệm.
Cho $x$, $y$ là các số thực dương thỏa mãn \({5^{x + 2y}} + \dfrac{3}{{{3^{xy}}}} + x + 1 = \dfrac{{{5^{xy}}}}{5} + {3^{ - x - 2y}} + y(x - 2)\). Tìm giá trị nhỏ nhất của biểu thức \(T = x + y\).
Theo đề ra ta có
\(\begin{array}{l}{5^{x + 2y}} + \dfrac{3}{{{3^{xy}}}} + x + 1 = \dfrac{{{5^{xy}}}}{5} + {3^{ - x - 2y}} + y(x - 2)\\ \Leftrightarrow {5^{x + 2y}} - \dfrac{1}{{{3^{x + 2y}}}} + x + 2y = {5^{xy - 1}} - \dfrac{1}{{{3^{xy - 1}}}} + xy - 1\end{array}\)
Xét \(f\left( t \right) = {5^t} - \dfrac{1}{{{3^t}}} + t\).\( \Rightarrow f'\left( t \right) = {5^t}\ln 5 + {3^{ - t}}\ln 3 + 1 > 0\)
\( \Rightarrow x + 2y = xy - 1 \Rightarrow y = \dfrac{{x + 1}}{{x - 2}}\).
Do \(y > 0,x > 0 \Rightarrow \dfrac{{x + 1}}{{x - 2}} > 0 \Rightarrow x > 2\)
Ta có: \(T = x + y = x + \dfrac{{x + 1}}{{x - 2}} = \dfrac{{{x^2} - x + 1}}{{x - 2}}\)
$T' = \dfrac{{{x^2} - 4x + 1}}{{{{\left( {x - 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 3 \in \left( {2; + \infty } \right)\\x = 2 - \sqrt 3 \notin \left( {2; + \infty } \right)\end{array} \right.$
Bảng biến thiên
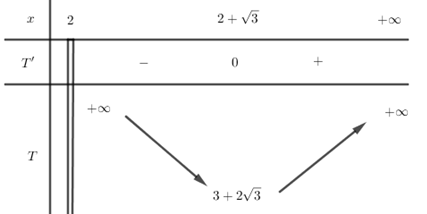
Từ bảng biến thiên ta thấy \({T_{\min }} = 3 + 2\sqrt 3 \) tại \(x = 2 + \sqrt 3 \).
Có bao nhiêu số nguyên dương \(a\) (\(a\) là tham số) để phương trình \(\left( {3{a^2} + 12a + 15} \right){\log _{27}}\left( {2x - {x^2}} \right) + \left( {\dfrac{9}{2}{a^2} - 3a + 1} \right){\log _{\sqrt {11} }}\left( {1 - \dfrac{{{x^2}}}{2}} \right) = 2{\log _9}\left( {2x - {x^2}} \right) + {\log _{11}}\left( {\dfrac{{2 - {x^2}}}{2}} \right)\) có nghiệm duy nhất?
Điều kiện \(0 < x < \sqrt 2 .\)
\(PT \Leftrightarrow \left( {{a^2} + 4a + 5} \right){\log _3}\left( {2x - {x^2}} \right) + \left( {9{a^2} - 6a + 2} \right){\log _{11}}\left( {\dfrac{{2 - {x^2}}}{2}} \right) = {\log _3}\left( {2x - {x^2}} \right) + {\log _{11}}\left( {\dfrac{{2 - {x^2}}}{2}} \right)\) \( \Leftrightarrow \left( {{a^2} + 4a + 4} \right){\log _3}\left( {2x - {x^2}} \right) + \left( {9{a^2} - 6a + 1} \right){\log _{11}}\left( {\dfrac{{2 - {x^2}}}{2}} \right) = 0\)
$ \Leftrightarrow {\left( {a + 2} \right)^2}{\log _3}\left( {2x - {x^2}} \right) + {\left( {3a - 1} \right)^2}{\log _{11}}\left( {\dfrac{{2 - {x^2}}}{2}} \right) = 0$$ \Leftrightarrow {\left( {\dfrac{{3a - 1}}{{a + 2}}} \right)^2} = \dfrac{{{{\log }_3}\left( {2x - {x^2}} \right)}}{{{{\log }_{11}}\left( {\dfrac{2}{{2 - {x^2}}}} \right)}} $$\left( * \right)$
Mà vế trái của $\left( * \right)$ luôn dương với mọi \(a\) nguyên dương
Vì \(0 < x < \sqrt 2 \) nên \(2 - {x^2} < 2 \Rightarrow \dfrac{2}{{2 - {x^2}}} > 1 \Rightarrow {\log _{11}}\left( {\dfrac{2}{{2 - {x^2}}}} \right) > 0\)
Do đó từ $\left( * \right)$ suy ra ${\log _3}\left( {2x - {x^2}} \right) > 0$$ \Leftrightarrow 2x - {x^2} > 1 \Leftrightarrow {x^2} - 2x + 1 < 0$$ \Rightarrow $ không tồn tại $x$.
Vậy không có giá trị \(a\) thỏa yêu cầu.
Xét các số thực dương \(x,\,\,y\) thỏa mãn \({\log _{\sqrt 3 }}\dfrac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x - 3} \right) + y\left( {y - 3} \right) + xy.\) Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức \(P = \dfrac{{3x + 2y + 1}}{{x + y + 6}}.\)
Ta có:
\({\log _{\sqrt 3 }}\dfrac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x - 3} \right) + y\left( {y - 3} \right) + xy\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) - {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right)\)\( = {x^2} + {y^2} + xy - 3\left( {x + y} \right)\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) + 3\left( {x + y} \right)\)\( = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + {x^2} + {y^2} + xy\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left( {x + y} \right) + 3\left( {x + y} \right) + 2\) \( = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + \left( {{x^2} + {y^2} + xy + 2} \right)\)
$ \Leftrightarrow {\log _{\sqrt 3 }}\left[ {3\left( {x + y} \right)} \right] + 3\left( {x + y} \right)$$ = {\log _{\sqrt 3 }}\left( {{x^2} + {y^2} + xy + 2} \right) + {x^2} + {y^2} + xy + 2$
Xét hàm số \(f\left( t \right) = {\log _{\sqrt 3 }}t + t\), \(t > 0\) có \(f'\left( t \right) = \dfrac{1}{{t\ln \sqrt 3 }} + 1 > 0,\,\,\forall t > 0\)
Vậy hàm số \(f\left( t \right)\) luôn đồng biến và liên tục trên khoảng $\left( {0; + \infty } \right)$
Do đó: \(f\left( {3\left( {x + y} \right)} \right) = f\left( {{x^2} + {y^2} + xy + 2} \right)\)\( \Leftrightarrow 3\left( {x + y} \right) = {x^2} + {y^2} + xy + 2\) \(\left( 1 \right)\)
\( \Leftrightarrow xy = {\left( {x + y} \right)^2} - 3\left( {x + y} \right) + 2\)
Ta có \(x = x + xy - xy = x\left( {y + 1} \right) - xy \le {\left( {\dfrac{{x + y + 1}}{2}} \right)^2} - xy\)
Đẳng thức xảy ra khi và chỉ khi \(x = y + 1\).
Do đó từ $\left( 1 \right)$, suy ra: \(x \le \dfrac{{{{\left( {x + y + 1} \right)}^2}}}{4} - {\left( {x + y} \right)^2} + 3\left( {x + y} \right) - 2\).
Đặt \(t = x + y\), \(t > 0\)
Suy ra: $P = \dfrac{{2\left( {x + y} \right) + 1 + x}}{{x + y + 6}} \le \dfrac{{2t + 1 + \dfrac{{{{\left( {t + 1} \right)}^2}}}{4} - {t^2} + 3t - 2}}{{t + 6}} = \dfrac{{ - 3{t^2} + 22t - 3}}{{4\left( {t + 6} \right)}} = f\left( t \right)$
Ta có: \(f'\left( t \right) = \dfrac{{ - 3{t^2} - 36t + 135}}{{4{{\left( {t + 6} \right)}^2}}} = 0 \Leftrightarrow t = 3\) (vì $t>0$)
Bảng biến thiên:
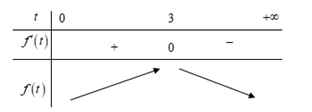
Dựa vào BBT, ta có \(\max P = \mathop {\max }\limits_{\left( {0; + \infty } \right)} f\left( t \right) = f\left( 3 \right) = 1\) khi và chỉ khi \(\left\{ \begin{array}{l}x = y + 1\\x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\).
Gọi $S$ là tập hợp tất cả các giá trị của $m$ sao cho $10m \in \mathbb{Z}$ và phương trình $2{\log _{mx - 5}}\left( {2{x^2} - 5x + 4} \right) = {\log _{\sqrt {mx - 5} }}\left( {{x^2} + 2x - 6} \right)$ có nghiệm duy nhất. Tìm số phần tử của $S.$
Ta có: $2{x^2} - 5x + 4 > 0$ với mọi $x$ nên phương trình
$2{\log _{mx - 5}}\left( {2{x^2} - 5x + 4} \right) = {\log _{\sqrt {mx - 5} }}\left( {{x^2} + 2x - 6} \right)$ tương đương với
$\left\{ \begin{array}{l}mx - 5 > 0\\mx - 5 \ne 1\\2{x^2} - 5x + 4 > 0\\2{x^2} - 5x + 4 = {x^2} + 2x - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}mx > 5\\mx \ne 6\\\left[ \begin{array}{l}x = 2\\x = 5\end{array} \right.\end{array} \right.$
Phương trình có nghiệm duy nhất tương đương với ta nhận nghiệm $x = 2$ và loại $x = 5$ hoặc nhận nghiệm $x = 5$ và loại $x = 2$.
+ Trường hợp 1: Nhận nghiệm $x = 2$ và loại $x = 5$.
Điều này tương đương với $\left\{ \begin{array}{l}2m > 5\\2m \ne 6\\\left[ \begin{array}{l}5m \le 5\\5m = 6\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{5}{2}\\m \ne 3\\\left[ \begin{array}{l}m \le 1\\m = \dfrac{6}{5}\end{array} \right.\end{array} \right.$ (vô lí)
+ Trường hợp 2: Nhận nghiệm $x = 5$ và loại $x = 2$.
Điều này tương đương với $\left\{ \begin{array}{l}5m > 5\\5m \ne 6\\\left[ \begin{array}{l}2m \le 5\\2m = 6\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\m \ne \dfrac{6}{5}\\\left[ \begin{array}{l}m \le \dfrac{5}{2}\\m = 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\\left\{ \begin{array}{l}1 < m \le \dfrac{5}{2}\\m \ne \dfrac{6}{5}\end{array} \right.\end{array} \right.$
Suy ra: $\left[ \begin{array}{l}10m = 30\\\left\{ \begin{array}{l}10 < 10m \le 25\\m \ne 12\end{array} \right.\end{array} \right.$
Vì $10m \in \mathbb{Z}$ nên $10m \in \left\{ {11;13;14...;25} \right\} \cup \left\{ {30} \right\}$
Trong tập hợp này có $15$ phần tử nên tập hợp $S$ cũng có $15$ phần tử.
Chú ý: $m \in \left\{ {\dfrac{{11}}{{10}};\dfrac{{13}}{{10}};\dfrac{{14}}{{10}}...;\dfrac{{25}}{{10}}} \right\} \cup \left\{ {\dfrac{{30}}{{10}}} \right\}$
Xét các số thực \(a\), \(b\) thỏa mãn điều kiện \(\dfrac{1}{3} < b < a < 1\). Tìm giá trị nhỏ nhất của biểu thức $P = {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) + 12\log _{\frac{b}{a}}^2a - 3$.
$P = {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) + 12{\left( {{{\log }_{\frac{b}{a}}}a} \right)^2} - 3$$ = {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) + 12{\left( {\dfrac{1}{{{{\log }_a}\dfrac{b}{a}}}} \right)^2} - 3$$ = {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) + 12{\left( {\dfrac{1}{{{{\log }_a}b - 1}}} \right)^2} - 3$
Ta có: $\dfrac{{3b - 1}}{4} \le {b^3}$$ \Leftrightarrow 3b - 1 \le 4{b^3}$$ \Leftrightarrow 4{b^3} - 3b + 1 \ge 0$$ \Leftrightarrow \left( {b + 1} \right)\left( {4{b^2} - 4b + 1} \right) \ge 0$
$ \Leftrightarrow \left( {b + 1} \right){\left( {2b - 1} \right)^2} \ge 0$ (luôn đúng với \(\dfrac{1}{3} < b < 1\))
$ \Rightarrow {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) \ge {\log _a}{b^3}$ ( vì \(a < 1\)) $ \Rightarrow {\log _a}\left( {\dfrac{{3b - 1}}{4}} \right) \ge 3{\log _a}b$
Do đó $P \ge 3{\log _a}b + \dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}} - 3$$ \Leftrightarrow P \ge 3\left( {{{\log }_a}b - 1} \right) + \dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}}$ \(\left( * \right)\)
Vì \(\dfrac{1}{3} < b < a < 1\) nên \({\log _a}b > 1\)
Áp dụng bất đẳng thức Côsi cho \(3\) số dương: \(\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right)\), \(\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right)\), $\dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}}$
\(\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right) + \dfrac{3}{2}\left( {{{\log }_a}b - 1} \right) + \dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}}\)\( \ge 3.\,\sqrt[3]{{\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right).\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right).\dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}}}}\)
\( \Leftrightarrow 3\left( {{{\log }_a}b - 1} \right) + \dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}} \ge 9\) \(\left( {**} \right)\)
Từ \(\left( * \right)\)và \(\left( {**} \right)\) ta có \(P \ge 9\)
Dấu bằng xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}b = \dfrac{1}{2}\\\dfrac{3}{2}\left( {{{\log }_a}b - 1} \right) = \dfrac{{12}}{{{{\left( {{{\log }_a}b - 1} \right)}^2}}}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{1}{2}\\{\left( {{{\log }_a}b - 1} \right)^3} = 8\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{1}{2}\\{\log _a}b - 1 = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{1}{2}\\{\log _a}b = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{1}{2}\\b = {a^3}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{1}{2}\\a = \sqrt[3]{b} = \sqrt[3]{{\dfrac{1}{2}}}\end{array} \right.\)
Vậy \(\min P = 9\)
Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền \(T\) theo hình thức lãi kép với lãi suất \(0,6\% \) mỗi tháng. Biết đến cuối tháng thứ $15$ thì người đó có số tiền là $10$ triệu đồng. Hỏi số tiền \(T\) gần với số tiền nào nhất trong các số sau?
Gọi \({A_k}\) là số tiền người đó cuối tháng thứ \(k\), đặt \(r = 0,6\% \).
Ta có \({A_1} = T\left( {1 + r} \right)\).
\({A_2} = \left( {{A_1} + T} \right)\left( {1 + r} \right) = T{\left( {1 + r} \right)^2} + T\left( {1 + r} \right)\).
\({A_3} = \left( {{A_2} + T} \right)\left( {1 + r} \right) = T{\left( {1 + r} \right)^3} + T{\left( {1 + r} \right)^2} + T\left( {1 + r} \right) = T\left( {1 + r} \right).\dfrac{{{{\left( {1 + r} \right)}^3} - 1}}{r}\).
\({A_{15}} = T\left( {1 + r} \right).\dfrac{{{{\left( {1 + r} \right)}^{15}} - 1}}{r}\)
\( \Rightarrow T = \dfrac{{{A_{15}}.r}}{{\left( {1 + r} \right)\left[ {{{\left( {1 + r} \right)}^{15}} - 1} \right]}} = \dfrac{{10 \times {{10}^6} \times 0,6\% }}{{1,006 \times \left( {{{1,006}^{15}} - 1} \right)}} \approx 635.301\) đồng
Cho $0 \le x;y \le 1$ thỏa mãn ${2017^{1 - x - y}} = \dfrac{{{x^2} + 2018}}{{{y^2} - 2y + 2019}}$. Gọi $M$, $m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S = \left( {4{x^2} + 3y} \right)\left( {4{y^2} + 3x} \right) + 25xy\). Khi đó $M + m$ bằng bao nhiêu?
Ta có ${2017^{1 - x - y}} = \dfrac{{{x^2} + 2018}}{{{y^2} - 2y + 2019}}$ $ \Leftrightarrow $ $\dfrac{{{{2017}^{1 - y}}}}{{{{2017}^x}}} = \dfrac{{{x^2} + 2018}}{{{{\left( {1 - y} \right)}^2} + 2018}}$
$ \Leftrightarrow {2017^{1 - y}}\left[ {{{\left( {1 - y} \right)}^2} + 2018} \right]$$ = {2017^x}\left( {{x^2} + 2018} \right)$
Xét hàm số $f\left( t \right) = {2017^t}\left( {{t^2} + 2018} \right)$, với $0 \le t \le 1$.
$ \Rightarrow $ $f'\left( t \right) = \left( {{t^2} + 2018} \right){.2017^t}.\ln 2017 + 2t{.2017^t}$ $ = {2017^t}\left[ {\left( {{t^2} + 2018} \right).\ln 2017 + 2t} \right] > 0, \forall x \in [0;1]$
$ \Rightarrow $ Hàm số $f\left( t \right)$ đồng biến trên $[0;1]$
$ \Rightarrow $ $1 - y = x$ $ \Leftrightarrow $ $y = 1 - x$
Theo giả thiết \(S = \left( {4{x^2} + 3y} \right)\left( {4{y^2} + 3x} \right) + 25xy\)
\(\begin{array}{l} = \left[ {4{x^2} + 3\left( {1 - x} \right)} \right].\left[ {4{{\left( {1 - x} \right)}^2} + 3x} \right] + 25x\left( {1 - x} \right)\\ = \left( {4{x^2} - 3x + 3} \right)\left( {4{x^2} - 5x + 4} \right) + 25x\left( {1 - x} \right)\\ = 16{x^4} - 20{x^3} + 16{x^2} - 12{x^3} + 15{x^2} - 12x + 12{x^2} - 15x + 12 + 25x - 25{x^2}\\ = 16{x^4} - 32{x^3} + 18{x^2} - 2x + 12\end{array}\)
Xét hàm số \(S\left( x \right) = 16{x^4} - 32{x^3} + 18{x^2} - 2x + 12\), với $0 \le x \le 1$.
$ \Rightarrow $ $S'\left( x \right) = 64{x^3} - 96{x^2} + 36x - 2$. Cho $S'\left( x \right) = 0$ $ \Leftrightarrow $ $\left[ \begin{array}{l}x = \dfrac{{2 \pm \sqrt 3 }}{4}\\x = \dfrac{1}{2}\end{array} \right.$
Bảng biến thiên
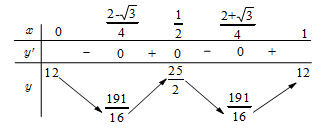
Từ bảng biến thiên, ta có $\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ {0;1} \right]} S\left( x \right) = \dfrac{{25}}{2}\\m = \mathop {\min }\limits_{\left[ {0;1} \right]} S\left( x \right) = \dfrac{{191}}{{16}}\end{array} \right.$.
Vậy $M + m = \dfrac{{25}}{2} + \dfrac{{191}}{{16}} = \dfrac{{391}}{{16}}$.
