Tập xác định của hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) là:
Hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\)xác định khi và chỉ khi \(x - 1 \ne 0 \Leftrightarrow x \ne 1\).
Vậy tập xác định của hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) là: \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x - 1}}\) có tâm đối xứng là
Đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x - 1}}\) có:
+) TCĐ: x=1
+) TCN: y=3
Tâm đối xứng là giao điểm hai đường tiệm cận nên \(I\left( { 1;\;3} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên
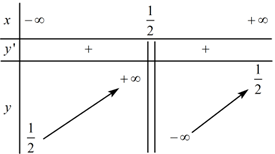
Hàm số \(y = f\left( x \right)\) là hàm nào dưới đây?
Dựa vào BBT ta có \(\mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = \infty \Rightarrow x = \frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = \frac{1}{2} \Rightarrow y = \frac{1}{2}\) là tiệm cận ngang của đồ thị hàm số.
\( \Rightarrow \) loại đáp án C và D.
Lại thấy hàm số đồng biến trên \(\left( { - \infty ;\,\,\frac{1}{2}} \right)\) và \(\left( {\frac{1}{2}; + \infty } \right)\)
+) Xét đáp án A: \(y = \frac{{x + 2}}{{2x - 1}}\) ta có:\(y' = \frac{{ - 1 - 2.2}}{{{{\left( {2x - 1} \right)}^2}}} = - \frac{5}{{{{\left( {2x - 1} \right)}^2}}} < 0 \Rightarrow \) loại đáp án A.
\( \Rightarrow y = \frac{{x - 2}}{{2x - 1}}\) là hàm số cần tìm.
Cho hàm số \(y = \frac{{ax + b}}{{x + c}}\) có đồ thị như hình vẽ
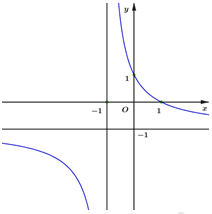
Tính giá trị của \(a + 2b + c.\)
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCĐ: \(x = - 1 \Rightarrow c = 1.\)
Đồ thị hàm số có TCN: \(y = - 1 \Rightarrow a = - 1.\)
\( \Rightarrow y = \frac{{ - x + b}}{{x + 1}}.\)
Đồ thị hàm số đi qua điểm \(\left( {0;\,\,1} \right) \Rightarrow b = 1.\)
\( \Rightarrow a + 2b + c = - 1 + 2.1 + 1 = 2.\)
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ bên.
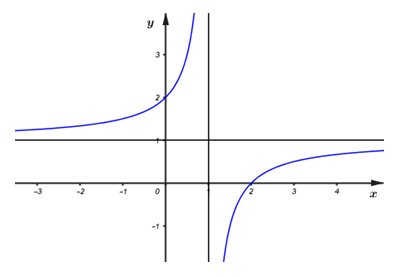
Khẳng định nào dưới đây là khẳng định đúng?
Dựa vào đồ thị hàm số ta thấy hàm số có TCĐ là: \(x = 1 \Rightarrow - \dfrac{d}{c} = 1 \Rightarrow d = - c \Rightarrow dc < 0.\)
Đồ thị hàm số có TCN là: \(y = 1 \Rightarrow \dfrac{a}{c} = 1 \Rightarrow a = c \Rightarrow ac > 0 \Rightarrow \) loại đáp án D.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \(2 \Rightarrow \dfrac{b}{d} = 2 \Leftrightarrow b = 2d \Rightarrow bd > 0 \Rightarrow \) loại đáp án C.
Ta có: \(\left\{ \begin{array}{l}dc < 0\\ac > 0\\bd > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}ad < 0\\bd > 0\end{array} \right. \Rightarrow ab < 0.\)
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) . Trong các mệnh đề sau, mệnh đề nào sai?
+ Đáp án A : Xét phương trình hoành độ giao điểm \(\frac{{2x - 1}}{{x + 1}} = 0 \Rightarrow x = \frac{1}{2}\) nên đồ thị hàm số cắt trục hoành tại điểm có hoành độ \(x = \frac{1}{2}\). Do đó A đúng.
+ Đáp án B: Đồ thị số có tiệm cận ngang là: \(y = \frac{2}{1} = 2\). Do đó B đúng.
+ Đáp án C: Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) có ĐK: \(x \ne - 1\) nên nó gián đoạn tại \(x = - 1\) nên C đúng.
+ Đáp án D: Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) có \(y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}} > 0;\,\forall x \ne - 1\) nên nó đồng biến trên từng khoảng xác định \(\left( { - \infty ; - 1} \right);\,\left( { - 1; + \infty } \right)\). Do đó D sai vì ta không thể nói đồng biến trên tập xác định của hàm số.
Hình vẽ dưới là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}(ad - bc \ne \) . Mệnh đề nào sau đây là đúng?
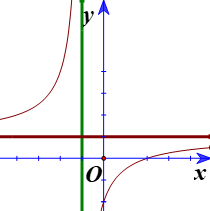
Bước 1: Xác định giao điểm với trục hoành và đánh giá ab.
Từ đồ thị suy ra đồ thị hàm số đã cho cắt trục hoành tại điểm có hoành độ dương.
Mặt khác, từ \(y = \dfrac{{ax + b}}{{cx + d}}\) suy ra đồ thị hàm số đã cho cắt trục hoành tại điểm \(A\left( { - \dfrac{b}{a};0} \right)\).
Từ đồ thị hàm số suy ra \( - \dfrac{b}{a} > 0 \Rightarrow ab < 0\).
Bước 2: Từ các đường tiệm cận suy ra tích ad.
Từ hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) suy ra đồ thị có các đường tiệm cận ngang và đứng lần lượt là:
\( = \dfrac{a}{c};x = - \dfrac{d}{c}\)
Từ đồ thị hàm số suy ra \(\left\{ {\begin{array}{*{20}{l}}{\dfrac{a}{c} > 0}\\{ - \dfrac{d}{c} < 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ac > 0}\\{dc > 0}\end{array}} \right.} \right.\)
\( \Rightarrow ad{c^2} > 0 \Rightarrow ad > 0\).
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có tập xác định là:
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TXĐ là \(D = R\backslash \left\{ { - \dfrac{d}{c}} \right\}\).
Hàm số \(y = \dfrac{{\sqrt {{x^2} - 2x + 1} }}{{x - 1}}\) xác định khi
Hàm số xác định khi \(\left\{ \begin{array}{l}{x^2} - 2x + 1 \ge 0\\x - 1 \ne 0\end{array} \right. \Leftrightarrow x \ne 1\) do \({x^2} - 2x + 1 = {\left( {x - 1} \right)^2} \ge 0\)
Số cực trị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) là:
Hàm phân thức bậc nhất trên bậc nhất không có cực trị.
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{5x + 1}}{{3x - 2}}\) là
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{5x + 1}}{{3x - 2}}\) là \(x = \dfrac{2}{3}\)
Cho hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$. Khẳng định nào dưới đây là đúng?
Xét hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$:
+) $\mathop {\lim }\limits_{x \to {2^ + }} {\mkern 1mu} \dfrac{{2x + 1}}{{x - 2}} = + \infty ,{\mkern 1mu} {\mkern 1mu} \mathop {\lim }\limits_{x \to {2^ - }} {\mkern 1mu} \dfrac{{2x + 1}}{{x - 2}} = - \infty \Rightarrow $
Đồ thị hàm số có tiệm cận đứng là$x = 2$. Phương án A: đúng.
+) $y' = - \dfrac{5}{{{{(x - 2)}^2}}} < 0,{\mkern 1mu} {\mkern 1mu} \forall x \ne 2 \Rightarrow $ Hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$ không có cực trị và hàm số nghịch biến trên các khoảng $\left( { - \infty ;2} \right);{\mkern 1mu} {\mkern 1mu} \left( {2; + \infty {\rm{\;}}} \right)$. Phương án B và D: sai.
+) Ta có: $3 = \dfrac{{2.1 + 1}}{{1 - 2}}$ vô lí $ \Rightarrow $Đồ thị hàm số không đi qua điểm$A(1;3)$. Phương án C: sai.
Tâm đối xứng của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) là:
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) nhận giao điểm của hai đường tiệm cận làm tâm đối xứng nên \(I\left( { - \dfrac{d}{c};\dfrac{a}{c}} \right)\).
Đề thi THPT QG - 2021 - mã 103
Biết hàm số \(y = \dfrac{{x + a}}{{x - 1}}\) (\(a\) là số thực cho trước, \(a \ne - 1\)) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
+ Từ đồ thị ta nhận thấy hàm số đồng biến trên mỗi khoảng xác định \( \Rightarrow y' > 0\).
+ Do hàm số \(y = \dfrac{{x + a}}{{x - 1}}\) không xác định tại \(x = 1\) \( \Rightarrow y' > 0\,\,\forall x \ne 1\).
Tâm đối xứng của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là:
Đồ thị hàm số có tiệm cận đứng \(x = \dfrac{3}{2}\) và tiệm cận ngang \(y = - \dfrac{1}{2}\)
Tâm đối xứng của đồ thị hàm số chính là giao điểm của hai đường tiệm cận.
Giao điểm hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là \(\left( {\dfrac{3}{2}; - \dfrac{1}{2}} \right)\) nên tâm đối xứng là \(\left( {\dfrac{3}{2}; - \dfrac{1}{2}} \right)\)
Đường cong của hình vẽ bên là đồ thị của hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ với $a,{\mkern 1mu} {\mkern 1mu} b,{\mkern 1mu} {\mkern 1mu} c,{\mkern 1mu} {\mkern 1mu} d$ là các số thực. Mệnh đề nào sau đây là đúng ?
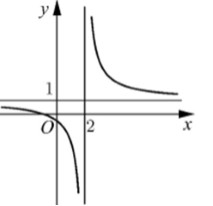
Dựa vào hình vẽ, ta thấy đồ thị hàm số có tiệm cận đứng $x = 2$ và đi xuống.
Vậy hàm số nghịch biến trên khoảng $\left( { - {\mkern 1mu} \infty ;2} \right)$ và $\left( {2; + {\mkern 1mu} \infty } \right)$$ \Rightarrow $$y' < 0,{\mkern 1mu} {\mkern 1mu} \forall x \ne 2.$
Bảng biến thiên sau đây là của hàm số nào?
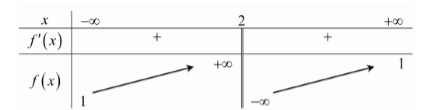
Quan sát bảng biến thiên ta thấy:
- Đồ thị hàm số nhận đường thẳng \(x = 2\) làm TCĐ, đường thẳng \(y = 1\) là tiệm cận ngang nên loại B và D.
Lại có, hàm số đồng biến trên các khoảng xác định.
Xét đáp án A:
Có \(f'\left( x \right) = \dfrac{{ - 2 + 3}}{{{{\left( {x - 2} \right)}^2}}} = \dfrac{1}{{{{\left( {x - 2} \right)}^2}}} > 0,\forall x \ne 2\).
Do đó hàm số đồng biến trên các khoảng xác định, phù hợp với các yêu cầu ở trên.
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
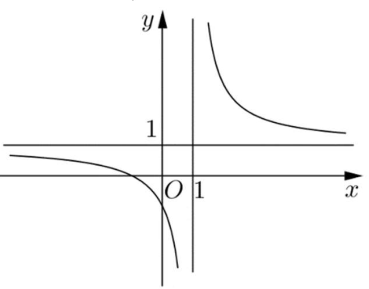
Từ đồ thị hàm số ta xác định được đây là đồ thị của hàm số dạng \(y = \dfrac{{ax + b}}{{cx + d}}\) nên loại C và D.
Nhận thấy đồ thị hàm số trên hình nhận \(y = 1\) làm TCN và \(x = 1\) làm TCĐ
+ Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) nhận \(y = 2\) làm TCN và \(x = 1\) làm TCĐ nên loại A.
+ Đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) nhận \(y = 1\) làm TCN và \(x = 1\) làm TCĐ nên chọn B.
Đề thi THPT QG – 2021 lần 1– mã 104
Biết hàm số \(y = \dfrac{{x + a}}{{x - 1}}\) \((a\) là số thực cho trước, \(a \ne 1)\) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
Ta có đồ thị hàm số có đường cong đi xuống nên \(y' < 0,\,\forall x \ne 1\)
Bảng biến thiên dưới đây là bảng biến thiên của hàm số nào:
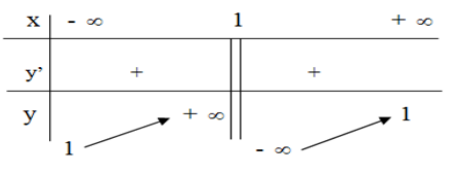
Từ BBT ta có hàm số đồng biến trên từng khoảng xác định và $\mathop {\lim }\limits_{x \to \pm \infty } y = 1,\mathop {\lim }\limits_{x \to 1} y = \infty $ nên đồ thị hàm số có tiệm cận ngang \(y=1\), tiệm cận đứng \(x=1\).
+) Hàm số \(y=\dfrac{x-2}{x-1}\) có \({y}'=\dfrac{1}{{{\left( x-1 \right)}^{2}}}>0\,\,\forall x\ne 1\), có \(y=1\) là tiệm cận ngang và \(x=1\) là tiệm cận đứng.


