Các bài toán liên quan đến lũy thừa với số mũ hữu tỉ.

Ta có: $T = 2{\left( {a + b} \right)^{ - 1}}.{\left( {ab} \right)^{\dfrac{1}{2}}}{\left[ {1 + \dfrac{1}{4}{{\left( {\sqrt {\dfrac{a}{b}}  - \sqrt {\dfrac{b}{a}} } \right)}^2}} \right]^{\dfrac{1}{2}}}$

$= \dfrac{2}{{a + b}}.\sqrt {ab} {\left[ {1 + \dfrac{1}{4}.{{\left( {\dfrac{{a - b}}{{\sqrt {ab} }}} \right)}^2}} \right]^{\dfrac{1}{2}}} = \dfrac{{2\sqrt {ab} }}{{a + b}}.\sqrt {1 + \dfrac{{{{\left( {a - b} \right)}^2}}}{{4ab}}}  = \dfrac{{2\sqrt {ab} }}{{a + b}}.\sqrt {\dfrac{{{{\left( {a + b} \right)}^2}}}{{4ab}}}  = 1$

Ta có

$P = \frac{{{a^{\frac{1}{3}}}\left( {{a^{\frac{1}{2}}} - {a^{\frac{5}{2}}}} \right)}}{{{a^{\frac{1}{4}}}\left( {{a^{\frac{7}{{12}}}} - {a^{\frac{{19}}{{12}}}}} \right)}} = \frac{{{a^{\frac{1}{3}}}.{a^{\frac{1}{2}}}\left( {1 - {a^{\frac{5}{2} - \frac{1}{2}}}} \right)}}{{{a^{\frac{1}{4}}}.{a^{\frac{7}{{12}}}}\left( {1 - {a^{\frac{{19}}{{12}} - \frac{7}{{12}}}}} \right)}} = \frac{{{a^{\frac{1}{3} + \frac{1}{2}}}\left( {1 - {a^2}} \right)}}{{{a^{\frac{1}{4} + \frac{7}{{12}}}}\left( {1 - a} \right)}} = \frac{{{a^{\frac{5}{6}}}\left( {1 - a} \right)\left( {1 + a} \right)}}{{{a^{\frac{{10}}{{12}}}}\left( {1 - a} \right)}} = 1 + a\,\,\left( {a > 0,\,a \ne 1} \right).$

Ta có $\sqrt[3]{{{a}^{5}}\sqrt[4]{a}}=\sqrt[3]{{{a}^{5}}.{{a}^{\frac{1}{4}}}}=\sqrt[3]{{{a}^{5+\frac{1}{4}}}}=\sqrt[3]{{{a}^{\frac{21}{4}}}}={{a}^{\frac{21}{12}}}={{a}^{\frac{7}{4}}}$.

Ta có 

$A = \dfrac{{\sqrt[3]{{{a^7}}}.{a^{\dfrac{{11}}{3}}}}}{{{a^4}.\sqrt[7]{{{a^{ - 5}}}}}} = \dfrac{{{a^{\dfrac{7}{3}}}.{a^{\dfrac{{11}}{3}}}}}{{{a^4}.{a^{ - \dfrac{5}{7}}}}} = \dfrac{{{a^6}}}{{{a^{\dfrac{{23}}{7}}}}} = {a^{\dfrac{{19}}{7}}} = {a^{\dfrac{{m}}{n}}} \Rightarrow \left\{ \begin{array}{l} m = 19\\ n = 7 \end{array} \right.$

Vậy ${{m}^{2}}-{{n}^{2}}=312.$

Ta có :

$P = \sqrt[5]{{{x^3}\,\sqrt[3]{{{x^2}\sqrt x }}}} = \sqrt[5]{{{x^3}\,\sqrt[3]{{{x^2}.{x^{\dfrac{1}{2}}}}}}} = \sqrt[5]{{{x^3}\,\sqrt[3]{{{x^{\dfrac{5}{2}}}}}}} = \sqrt[5]{{{x^3}\,.{{\left( {{x^{\dfrac{5}{2}}}} \right)}^{\dfrac{1}{3}}}}} = \sqrt[5]{{{x^{3 + \dfrac{5}{6}}}}} = {\left( {{x^{\dfrac{{23}}{6}}}} \right)^{\dfrac{1}{5}}} = {x^{\dfrac{{23}}{{30}}}}.$

Do $a>0,b>0$ ta chọn a = 1; b = 2 sau đó thay vào biểu thức T bấm máy tính ra kết quả

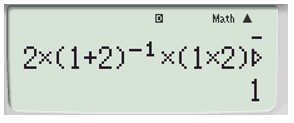
Vậy T = 1

$\begin{array}{l}\sqrt {a.\sqrt[3]{{{a^2}.\sqrt[4]{{\frac{1}{a}}}}}} :\sqrt[{24}]{{{a^7}}} = \sqrt {a.\sqrt[3]{{{a^2}.\frac{1}{{{a^{\frac{1}{4}}}}}}}} :{a^{\frac{7}{{24}}}} = \sqrt {a.\sqrt[3]{{{a^{\frac{7}{4}}}}}} :{a^{\frac{7}{{24}}}}\\ = \sqrt {a.{{\left( {{a^{\frac{7}{4}}}} \right)}^{\frac{1}{3}}}} :{a^{\frac{7}{{24}}}} = \sqrt {a.{a^{\frac{7}{{12}}}}} :{a^{\frac{7}{{24}}}} = {\left( {{a^{\frac{{19}}{{12}}}}} \right)^{\frac{1}{2}}}:{a^{\frac{7}{{24}}}} = {a^{\frac{{19}}{{24}} - \frac{7}{{24}}}} = {a^{\frac{1}{2}}}\end{array}$

Vậy m = 1 ; n = 2

Giá trị của ${{m}^{2}}+{{n}^{2}}={{1}^{2}}+{{2}^{2}}=5$

Ta có $A=\frac{{{a}^{\frac{1}{3}}}\sqrt{b}+{{b}^{\frac{1}{3}}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}=\frac{{{a}^{\frac{1}{3}}}{{b}^{\frac{1}{3}}}\left( \sqrt[6]{b}+\sqrt[6]{a} \right)}{\sqrt[6]{a}+\sqrt[6]{b}}={{a}^{\frac{1}{3}}}{{b}^{\frac{1}{3}}}=\sqrt[3]{ab}.$

${{x}^{\frac{4}{5}}}\sqrt[6]{{{x}^{5}}\sqrt{x}}$ $={{x}^{\frac{4}{5}}}\sqrt[6]{{{x}^{5}}{{x}^{\frac{1}{2}}}}$ $={{x}^{\frac{4}{5}}}\sqrt[6]{{{x}^{5+\frac{1}{2}}}}$ $={{x}^{\frac{4}{5}}}{{\left( {{x}^{\frac{11}{2}}} \right)}^{\frac{1}{6}}}$ $={{x}^{\frac{4}{5}}}{{x}^{\frac{11}{2}.\frac{1}{6}}}$ $={{x}^{\frac{4}{5}}}{{x}^{\frac{11}{12}}}$ $={{x}^{\frac{4}{5}+\frac{11}{12}}}$ $={{x}^{\frac{103}{60}}}={{x}^{m}}$ $\Rightarrow m=\dfrac{103}{60}$

$\begin{align}{{y}^{\frac{4}{5}}}:\sqrt[6]{{{y}^{5}}\sqrt{y}}={{y}^{\frac{4}{5}}}:\sqrt[6]{{{y}^{5}}{{y}^{\frac{1}{2}}}}\\={{y}^{\frac{4}{5}}}:\sqrt[6]{{{y}^{5+\frac{1}{2}}}}\\={{y}^{\frac{4}{5}}}:{{\left( {{y}^{\frac{11}{2}}} \right)}^{\frac{1}{6}}}={{y}^{\frac{4}{5}}}:{{y}^{\frac{11}{2}.\frac{1}{6}}}\\={{y}^{\frac{4}{5}}}:{{y}^{\frac{11}{12}}}={{y}^{\frac{4}{5}-\frac{11}{12}}}\\={{y}^{-\frac{7}{60}}}={{y}^{n}}\\\Rightarrow n=-\frac{7}{60} \\  \Rightarrow m-n=\frac{103}{60}-\frac{-7}{60}=\frac{11}{6} \\ \end{align}$

$0<2-\sqrt{2}<1\Rightarrow {{\left( 2-\sqrt{2} \right)}^{3}}>{{\left( 2-\sqrt{2} \right)}^{4}}\Rightarrow$Đáp án A sai.

$4-\sqrt{2}>1\Rightarrow {{\left( 4-\sqrt{2} \right)}^{3}}<{{\left( 4-\sqrt{2} \right)}^{4}}\Rightarrow$Đáp án B đúng.

$\sqrt{11}-\sqrt{2}>1\Rightarrow {{\left( \sqrt{11}-\sqrt{2} \right)}^{6}}<{{\left( \sqrt{11}-\sqrt{2} \right)}^{7}}\Rightarrow$ Đáp án C sai.

$0<\sqrt{3}-\sqrt{2}<1\Rightarrow {{\left( \sqrt{3}-\sqrt{2} \right)}^{4}}>{{\left( \sqrt{3}-\sqrt{2} \right)}^{5}}\Rightarrow$Đáp án D sai.

Ta chọn a = 2 sau đó chuyển vế phải sang nếu kết quả nào ra số dương thì đó là kết quả đúng.

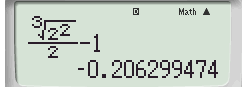
Đáp án A: (sai)

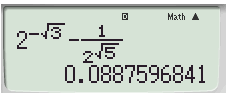
Đáp án B

Nên đáp án B đúng.

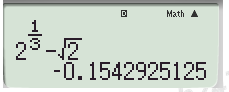
Đáp án C (sai)

Đáp án D.

$\frac{1}{{{a^{2016}}}} = {a^{ - 2016}};\frac{1}{{{a^{2017}}}} = {a^{ - 2017}}$

Do a > 1 mà $- 2016 >  - 2017 \Rightarrow {a^{ - 2016}} > {a^{ - 2017}}$

Nên D sai.

Vì $\sqrt 5  - 1 > 1$ nên ${\left( {\sqrt 5  - 1} \right)^m} < {\left( {\sqrt 5  - 1} \right)^n} \Leftrightarrow m < n$.

Vì $- \dfrac{1}{2} >  - \dfrac{3}{4}$ nên ${\left( {\sqrt a  - 2} \right)^{ - \dfrac{1}{2}}} \le {\left( {\sqrt a  - 2} \right)^{ - \dfrac{3}{4}}} \Leftrightarrow 0 < \sqrt a  - 2 \le 1 \Leftrightarrow 2 < \sqrt a  \le 3 \Leftrightarrow 4 < a \le 9$.

Vì $\dfrac{9}{4} > 2$ nên ${\left( {2 - \sqrt a } \right)^{\dfrac{9}{4}}} > {\left( {2 - \sqrt a } \right)^2} \Leftrightarrow 2 - \sqrt a  > 1 \Leftrightarrow 0 \le \sqrt a  < 1 \Leftrightarrow 0 \le a < 1$.

Với $x > 0$ ta có: $P = \sqrt[3]{{{x^5}\sqrt[4]{x}}} = \sqrt[3]{{{x^5}.{x^{\dfrac{1}{4}}}}}$$= \sqrt[3]{{{x^{5 + \dfrac{1}{4}}}}} = \sqrt[3]{{{x^{\dfrac{{21}}{4}}}}}$ $= {x^{\dfrac{{21}}{4}:3}} = {x^{\dfrac{7}{4}}}$

$\begin{array}{l}\,\,\,\,\left( {\dfrac{{{x^{\frac{1}{2}}} - {y^{\frac{1}{2}}}}}{{x{y^{\frac{1}{2}}} + {x^{\frac{1}{2}}}y}} + \dfrac{{{x^{\frac{1}{2}}} + {y^{\frac{1}{2}}}}}{{x{y^{\frac{1}{2}}} - {x^{\frac{1}{2}}}y}}} \right).\dfrac{{{x^{\frac{3}{2}}}{y^{\frac{1}{2}}}}}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \left( {\dfrac{{\sqrt x  - \sqrt y }}{{x\sqrt y  + \sqrt x .y}} + \dfrac{{\sqrt x  + \sqrt y }}{{x\sqrt y  - \sqrt x .y}}} \right).\dfrac{{x\sqrt x .\sqrt y }}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \left( {\dfrac{{\sqrt x  - \sqrt y }}{{\sqrt {xy} \left( {\sqrt x  + \sqrt y } \right)}} + \dfrac{{\sqrt x  + \sqrt y }}{{\sqrt {xy} \left( {\sqrt x  - \sqrt y } \right)}}} \right).\dfrac{{x\sqrt x .\sqrt y }}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \dfrac{{{{\left( {\sqrt x  - \sqrt y } \right)}^2} + {{\left( {\sqrt x  + \sqrt y } \right)}^2}}}{{\sqrt {xy} \left( {\sqrt x  + \sqrt y } \right)\left( {\sqrt x  - \sqrt y } \right)}}.\dfrac{{x\sqrt x .\sqrt y }}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \dfrac{{x - 2\sqrt {xy}  + y + x + 2\sqrt {xy}  + y}}{{\sqrt {xy} \left( {\sqrt x  + \sqrt y } \right)\left( {\sqrt x  - \sqrt y } \right)}}.\dfrac{{x\sqrt x .\sqrt y }}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \dfrac{{2\left( {x + y} \right)}}{{\left( {\sqrt x  + \sqrt y } \right)\left( {\sqrt x  - \sqrt y } \right)}}.\dfrac{x}{{x + y}} - \dfrac{{2y}}{{x - y}}\\ = \dfrac{{2x}}{{x - y}} - \dfrac{{2y}}{{x - y}}\\ = \dfrac{{2\left( {x - y} \right)}}{{x - y}} = 2\end{array}$

Ta có:

$\begin{array}{l}P = \dfrac{{\sqrt a  - \sqrt b }}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{\sqrt {4a}  + \sqrt[4]{{16ab}}}}{{\sqrt[4]{a} + \sqrt[4]{b}}}\\P = \dfrac{{{{\left( {\sqrt[4]{a}} \right)}^2} - {{\left( {\sqrt[4]{b}} \right)}^2}}}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{2\sqrt[4]{a}.\sqrt[4]{a} + 2\sqrt[4]{a}.\sqrt[4]{b}}}{{\sqrt[4]{a} + \sqrt[4]{b}}}\\P = \dfrac{{\left( {\sqrt[4]{a} - \sqrt[4]{b}} \right)\left( {\sqrt[4]{a} + \sqrt[4]{b}} \right)}}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \dfrac{{2\sqrt[4]{a}.\left( {\sqrt[4]{a} + \sqrt[4]{b}} \right)}}{{\sqrt[4]{a} + \sqrt[4]{b}}}\\P = \sqrt[4]{a} + \sqrt[4]{b} - 2\sqrt[4]{a}\\P = \sqrt[4]{b} - \sqrt[4]{a}\end{array}$

$\Rightarrow m =  - 1,\,\,n = 1$.

Vậy $m.n =  - 1$.

Ta có:

$\begin{array}{l}P = \left( {\dfrac{{{a^{\frac{1}{2}}} + 2}}{{a + 2{a^{\frac{1}{2}}} + 1}} - \dfrac{{{a^{\frac{1}{2}}} - 2}}{{a - 1}}} \right).\dfrac{{\left( {{a^{\frac{1}{2}}} + 1} \right)}}{{{a^{\frac{1}{2}}}}}\\P = \left( {\dfrac{{\sqrt a  + 2}}{{a + 2\sqrt a  + 1}} - \dfrac{{\sqrt a  - 2}}{{a - 1}}} \right).\dfrac{{\left( {\sqrt a  + 1} \right)}}{{\sqrt a }}\\P = \left( {\dfrac{{\sqrt a  + 2}}{{{{\left( {\sqrt a  + 1} \right)}^2}}} - \dfrac{{\sqrt a  - 2}}{{\left( {\sqrt a  - 1} \right)\left( {\sqrt a  + 1} \right)}}} \right).\dfrac{{\left( {\sqrt a  + 1} \right)}}{{\sqrt a }}\\P = \dfrac{{\left( {\sqrt a  + 2} \right)\left( {\sqrt a  - 1} \right) - \left( {\sqrt a  - 2} \right)\left( {\sqrt a  + 1} \right)}}{{\left( {\sqrt a  - 1} \right){{\left( {\sqrt a  + 1} \right)}^2}}}.\dfrac{{\left( {\sqrt a  + 1} \right)}}{{\sqrt a }}\\P = \dfrac{{a + \sqrt a  - 2 - a + \sqrt a  + 2}}{{\left( {\sqrt a  - 1} \right){{\left( {\sqrt a  + 1} \right)}^2}}}.\dfrac{{\left( {\sqrt a  + 1} \right)}}{{\sqrt a }}\\P = \dfrac{{2\sqrt a }}{{\left( {\sqrt a  - 1} \right)\left( {\sqrt a  + 1} \right)}}.\dfrac{1}{{\sqrt a }}\\P = \dfrac{2}{{\left( {\sqrt a  - 1} \right)\left( {\sqrt a  + 1} \right)}} = \dfrac{2}{{a - 1}}\end{array}$

$\Rightarrow m = 2,\,\,n =  - 1$ .

Vậy $2m - n = 2.2 - \left( { - 1} \right) = 5$.

Ta có:

$\begin{array}{l}P = \dfrac{{{a^{\frac{1}{3}}}\sqrt b  + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}} - \sqrt[3]{{ab}}\\P = \dfrac{{{a^{\frac{1}{3}}}.{b^{\frac{1}{2}}} + {b^{\frac{1}{3}}}.{a^{\frac{1}{2}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} - {\left( {ab} \right)^{\frac{1}{3}}}\\P = \dfrac{{{a^{\frac{1}{3}}}{b^{\frac{1}{3}}}\left( {{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}} \right)}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} - {\left( {ab} \right)^{\frac{1}{3}}}\\P = {\left( {ab} \right)^{\frac{1}{3}}} - {\left( {ab} \right)^{\frac{1}{3}}} = 0\end{array}$

Ta có: $\sqrt[{15}]{{{a^7}}} > \sqrt[5]{{{a^2}}} \Leftrightarrow {a^{\frac{7}{{15}}}} > {a^{\frac{2}{5}}}$.

Vì $\dfrac{7}{{15}} > \dfrac{2}{5}$, mà ${a^{\frac{7}{{15}}}} > {a^{\frac{2}{5}}}$ nên $a > 1$.