Cho số phức thỏa mãn |z−2i|≤|z−4i| và |z−3−3i|=1. Giá trị lớn nhất của P=|z−2| là
Lời giải chi tiết.Giả sử số phức thỏa mãn yêu cầu bài toán có dạng z=a+bi,(a,b∈). Khi đó ta có
{|z−2i|=|(a+bi)−2i|=√a2+(b−2)2|z−4i|=|(a+bi)−4i|=√a2+(b−4)2|z−3−3i|=|(a+bi)−3−3i|=√(a−3)2+(b−3)2|z−2|=|(a+bi)−2|=√(a−2)2+b2
Từ giả thiết ta suy ra
{√a2+(b−2)2≤√a2+(b−4)2(a−3)2+(b−3)2=1⇔{(b−2)2≤(b−4)2(a−3)2+(b−3)2=1⇔{[b−2≤b−4(VN)b−2≤−b+4(a−3)2+(b−3)2=1⇔{b≤3(a−3)2+(b−3)2=1.
Từ(a−3)2+(b−3)2=1⇒(a−3)2≤1⇒2≤a≤4⇒0≤a−2≤2.
Do đó P=|z−2|=√(a−2)2+b2≤√22+32=√13.
Đẳng thức xảy ra khi và chỉ khi
{(a−2)2=22b=3(a−3)2+(b−3)2=1⇔{a=4b=3.
Cho số phức z thỏa mãn |z2−2z+5|=|(z−1+2i)(z−1+3i)| và w=z−2+2i giá trị nhỏ nhất của |w| bằng ?
Ta có z2−2z+5=(z−1)2+4=(z−1)2−(2i)2=(z−1+2i)(z−1−2i)
Do đó |z2−2z+5|=|(z−1+2i)(z+3i−1)|
⇔|(z−1+2i)(z−1−2i)|=|(z−1+2i)(z+3i−1)|
⇔|z−1+2i||z−1−2i|=|z−1+2i||z+3i−1|⇔[|z−1+2i|=0|z−1−2i|=|z+3i−1|
TH1:
|z−1+2i|=0⇔z=1−2i⇒w=1−2i−2+2i=−1⇒|w|=1
TH2:
|z−1−2i|=|z+3i−1|
⇔|x−1+(y−2)i|=|x−1+(y+3)i|
với z=x+yi(x,y∈R).
⇔(x−1)2+(y−2)2=(x−1)2+(y+3)2
⇔y=−12 ⇒z=x−12i.
Khi đó |w|=|z−2+2i|=|x−2+32i|=√(x−2)2+94≥32.
Vậy min|w|=1.
Cho số phức z thỏa mãn điều kiện |z−1|=√2. Tìm giá trị lớn nhất của biểu thức
T=|z+i|+|z−2−i|
Tập hợp các điểm z thỏa mãn điều kiện |z−1|=√2 là đường tròn (C) tâm I(1;0) bán kính R=√2.
T=|z+i|+|z−2−i|=|z−(−1)|+|z−(2+i)|
Gọi M là điểm biểu diễn cho số phức z, A(0;−1) là điểm biểu diễn cho số phức −i, B(2;1) là điểm biểu diễn cho số phức 2+i. Dễ thấy A,B∈(C) và AB=√22+22=2√2=2R⇒AB là đường kính của đường tròn (C)⇒ΔMAB vuông tại M ⇒MA2+MB2=AB2=8⇒MB=√8−MA2
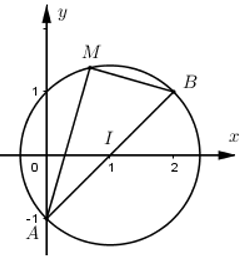
Ta có: T=|→OM−→OA|+|→OM−→OB|=MA+MB=MA+√8−MA2
Đặt MA=x(0≤x≤2√2), xét hàm số f(x)=x+√8−x2 trên [0;2√2] ta có:
f′(x)=1−x√8−x2=√8−x2−x√8−x2=0⇔√8−x2=x⇔8−x2=x2⇔x=2
f(0)=√2,f(2√2)=2√2;f(2)=4⇒max[0;2√2]f(x)=f(2)=4
Vậy maxT=4.
Xét số phức z thỏa mãn (1+2i)|z|=√10z−2+i. Mệnh đề nào dưới đây đúng?
(1+2i)|z|=√10z−2+i⇔(1+2i)|z|+2−i=√10z⇔(|z|+2)+(2|z|−1)i=√10z⇔(|z|+2)2+(2|z|−1)2=10|z|2⇔|z|2+4|z|+4+4|z|2−4|z|+1=10|z|2⇔5|z|4+5|z|2−10=0⇔|z|=1∈(12;32)
Cho số phức z thỏa mãn |z−2+3i|+|z+2+i|=4√5. Tính GTLN của P=|z−4+4i|
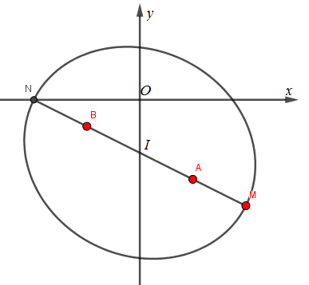
Cho số phức z=x+yi,(x,y∈R), S(x;y)là điểm biểu diễn của z trên hệ trục tọa độ Oxy.
|z−2+3i|+|z+2+i|=4√5⇔√(x−2)2+(y+3)2+√(x+2)2+(y+1)2=4√5(1)
Lấy các điểm A(2;−3),B(−2;−1). Phương trình (1) ⇔SA+SB=4√5
⇒ Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;−3),B(−2;−1) và có độ dài trục lớn là 2a=4√5⇒a=2√5.
Lấy M(4;−4). Dễ dàng kiểm tra được {→AB=2→MAMA+MB=4√5=2a
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB ⇒I(0;−2), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm S∈(E): SM≤MN=2a=4√5
SMmax=4√5khi và chỉ khi S trùng N ⇔Pmax=4√5 khi và chỉ khi S≡N(−4;0)⇔z=−4
Xét các số phức z=a+bi,(a;b∈R) thỏa mãn đồng thời hai điều kiện |z|=|¯z+4−3i| và |z+1−i|+|z−2+3i| đạt giá trị nhỏ nhất. Giá trị P=a+2b là:
Gọi z=x+yi ta có:
|x+yi|=|x−yi+4−3i|⇔x2+y2=(x+4)2+(y+3)2⇔8x+6y=−25
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(−1;1);B(2;−3) ta có:
|z+1−i|+|z−2+3i|=MA+MB nhỏ nhất.
Ta có : MA+MB≥2√MA.MB, dấu bằng xảy ra ⇔MA=MB⇒ M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có I(12;−1) và →AB=(3;−4)
Phương trình đường trung trực của AB là 3(x−12)−4(y+1)=0⇔3x−4y−112=0
Để (MA+MB)min⇔ Tọa độ điểm M là nghiệm của hệ phương trình
{8x+6y=−253x−4y=112⇔{x=−6750y=−11950
⇒z=−6750−11950i⇔{a=−6750b=−11950⇒P=a+2b=−6110
Cho số phức z thỏa mãn |z−3−4i|=√5. Gọi M,m lần lượt là giá trị lớn nhất, nhỏ nhất biểu thức P=|z+2|2−|z−i|2.
Đặt z=x+yi(x,y∈R) suy ra tập hợp các điểm M(z)=(x;y) là đường tròn (C) có tâm I(3;4) và bán kính R=√5. Ta có P=|z+2|2−|z−i|2=|x+2+yi|2−|x+(y−1)i|2=(x+2)2+y2−x2−(y−1)2
=x2+y2+4x+4−x2−y2+2y−1=4x+2y+3→(Δ):4x+2y+3−P=0.
Ta cần tìm P sao cho đường thẳng (Δ) và đường tròn (C) có điểm chung ⇔d(I;(Δ))≤R.
⇔|4.3+2.4+3−P|√42+22≤√5⇔|23−P|≤10⇔−10≤23−P≤10⇔13≤P≤33.
Do đó, {maxP=33minP=13⇒w=M+mi=33+13i. Vậy |w|=√1258.
Cho hai số phức z1,z2 thỏa mãn |z1|=2,|z2|=√3. Gọi M, N là các điểm biểu diễn cho z1 và iz2. Biết ^MON=300. Tính S=|z21+4z22| ?
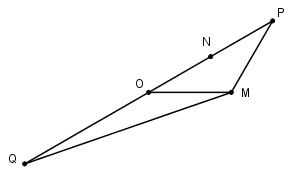
Đặt z3=iz2⇒z23=−z22⇒S=|z21+4z22|=|z21−4z23|=|z1−2z3||z1+2z3|M, N là các điểm biểu diễn cho z1,z3⇒OM=2,ON=|z3|=|iz2|=|i|.|z2|=√3.Gọi P là điểm biểu diễn cho 2z3 và Q là điểm biểu diễn cho −2z3 , ta có N là trung điểm của OP và P, Q đối xứng nhau qua O. Khi đó S=MP.MQ.
Áp dụng định lí Cosin trong ΔOMP có:
MP2=OP2+OM2−2OP.OM.cos30=12+4−2.2√3.2.√32=4⇒MP=2Áp dụng định lí Cosin trong ΔOMQ có:
MQ2=OM2+OQ2−2OM.OQ.cos1500=4+12+2.2.2√3.√32=2√7⇒S=MP.MQ=2.2√7=4√7
Cho hai số phức z1,z2 thỏa mãn |z1+1−i|=2 và z2=iz1. Tìm giá trị lớn nhất m của biểu thức |z1−z2|.
Ta có: |z1−z2|=|iz2−z2|=|z2(1−i)|=√2|z1|
Mà |z1|−|1−i|≤|z1+1−i|≤|z1|+|1−i|⇒|z1|−√2≤2≤|z1|+√2⇒2−√2≤|z1|≤2+√2
⇒√2(2−√2)≤√2|z1|≤√2(2+√2)⇒2√2−2≤√2|z1|≤2√2+2
Vậy M=2√2+2.
Cho số phức z thỏa mãn điều kiện |z−1−i|+|z+1+3i|=6√5. Giá trị lớn nhất của |z−2−3i| là
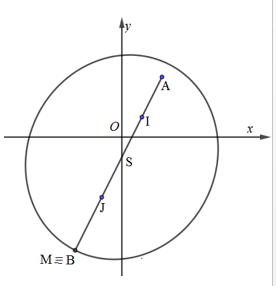
Gọi I(1;1),J(−1;−3),A(2;3). Xét số phức z=x+yi,(x,y∈R), có điểm biểu diễn là M(x;y).
|z−1−i|+|z+1+3i|=6√5
⇔√(x−1)2+(y−1)2+√(x+1)2+(y+3)2=6√5 (1)
⇔MI+MJ=6√5⇒Mdi chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là 3√5 (như hình vẽ).
Tìm giá trị lớn nhất của |z−2−3i| tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có: →IA=(1;2),→JA=(3;6)⇒→JA=3→IA, điểm A nằm trên trục lớn của elip.
⇒AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ ⇒S(0;−1).
Độ dài đoạn AB=SA+SB
Mà →AS=(−2;−4)⇒AS=2√5, SB=6√52=3√5 ⇒AB=5√5
Vậy |z−2−3i|max=5√5.
Cho hai số phức z1,z2 thỏa mãn |z1−3i+5|=2 và |iz2−1+2i|=4. Tìm giá trị lớn nhất của biểu thức T=|2iz1+3z2|.
Ta có |z1−3i+5|=2⇔|2i(z1−3i+5)|=2.|2i|⇔|2iz1+6+10i|=4.Và |iz2−1+2i|=4⇔|z2−1−2ii|=4⇔|z2+2+i|=4⇔|−3z2−6−3i|=12.Đặt {u=2iz1v=−3z2⇒{|u+6+10i|=4|v−6−3i|=12 và T=|2iz1+3z2|=|2iz1−(−3z2)|=|u−v|.Tập hợp điểm M biểu diễn số phức u là đường tròn (x+6)2+(y+10)2=16 tâm I1(−6;−10),R1=4.Tập hợp điểm N biểu diễn số phức v là đường tròn (x−6)2+(y−3)2=144 tâm I2(6;3),R2=12.
Khi đó T=MNmax⇔MN=I1I2+R1+R2=√122+132+4+12=√313+16.
Biết số phức z thỏa mãn |z−3−4i|=√5 và biểu thức T=|z+2|2−|z−i|2 đạt giá trị lớn nhất. Tính |z|?
Gọi z=x+yi⇒(x−3)2+(y−4)2=5(1)T=|x+yi+2|2−|x+yi−i|2=(x+2)2+y2−x2−(y−1)2=4x+2y+3=4(x−3)+2(y−4)+23Ta có: [4(x−3)+2(y−4)]2≤(42+22)[(x−3)2+(y−4)2]=180⇔4(x−3)+2(y−4)≤6√5Dấu bằng xảy ra ⇔x−34=y−42⇔x−3=2y−8⇔x=2y−5Thay vào (1) ta có:
(2y−8)2+(y−4)2=5⇔5(y−4)2=5⇔[y−4=1y−4=−1⇔[y=5y=3⇔[{x=5y=5{x=1y=3⇒[z=5+5iz=1+3iz=5+5i⇒T=33(TM)z=1+3i⇒T=13<33(KTM)
=>z=5+5i=> \left| z \right| =5 \sqrt {2}
Cho hai số phức z, w thỏa mãn \left\{ \begin{align} \left| z-3-2i \right|\le 1 \\ \left| \text{w}+1+2i \right|\le \left| \text{w}-2-i \right| \\ \end{align} \right.. Tìm GTNN {{P}_{\min }} của biểu thức P=\left| z-\text{w} \right|.
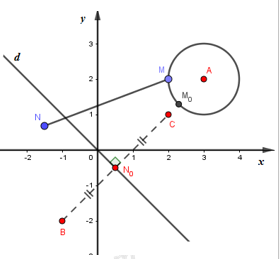
Đặt A(3;2),\,\,B(-1;-2),\,\,C(2;1). Gọi M, N lần lượt là điểm biểu diến của z, w.
Vì \left| z-3-2i \right|\le 1 nên tập hợp điểm biểu diễn của z trên hệ trục Oxy là hình tròn tâm A bán kính 1.
Vì \left| \text{w}+1+2i \right|\le \left| \text{w}-2-i \right| nên tập hợp điểm biểu diễn của w trên hệ trục Oxy là nửa mặt phẳng bờ d chứa B và đường thẳng d. Trong đó d là trung trực của đoạn thẳng BC.
P=\left| z-\text{w} \right|=MN, {{P}_{\min }}=M{{N}_{\min }}.
Dễ dàng kiểm tra được A, B, C thẳng hàng và MN ngắn nhất khi MN trùng với {{M}_{0}}{{N}_{0}}.
Trong đó, {{N}_{0}}: trung điểm của BC, {{M}_{0}}: giao của AB và đường tròn \left( A;1 \right).
Độ dài đoạn {{M}_{0}}{{N}_{0}}=d\left( A;d \right)-R=d(A;d)-1
*) Phương trình đường thẳng d:
{{N}_{0}} là trung điểm BC \Rightarrow {{N}_{0}}\left( \dfrac{1}{2};\dfrac{-1}{2} \right)
\overrightarrow{BC}=(3;3)\Rightarrow dcó 1 VTPT là \left( 1;1 \right)
Phương trình đường thẳng d: 1(x-\dfrac{1}{2})+1(y-\dfrac{-1}{2})=0\Leftrightarrow x+y=0
d\left( A;d \right)=\dfrac{\left| 3+2 \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}}=\dfrac{5}{\sqrt{2}}\Rightarrow {{M}_{o}}{{N}_{0}}=\dfrac{5}{\sqrt{2}}-1=\dfrac{5\sqrt{2}-2}{2}
Vậy, {{P}_{\min }}=\dfrac{5\sqrt{2}-2}{2}
Trong các số phức z thỏa mãn \left| {{z}^{2}}+1 \right|=2\left| z \right|, gọi z_1 và z_2 lần lượt là các số phức có môđun lớn nhất và nhỏ nhất. Khi đó môđun lớn nhất của số phức w={{z}_{1}}+{{z}_{2}} là:
Ta có
\begin{array}{l} \left| {{z^2} + 1} \right| = 2\left| z \right| \Leftrightarrow {\left| {{z^2} + 1} \right|^2} = 4{\left| z \right|^2} \Leftrightarrow \left( {{z^2} + 1} \right)\left( {\overline {{z^2} + 1} } \right) = 4z\overline z \\ \Leftrightarrow \left( {{z^2} + 1} \right)\left( {{{\overline z }^2} + 1} \right) = 4z\overline z \Leftrightarrow {\left( {z\overline z } \right)^2} + {z^2} + {\overline z ^2} + 1 - 4z\overline z = 0\\ \Leftrightarrow {\left( {z + \overline z } \right)^2} + {\left( {z\overline z } \right)^2} - 6z\overline z + 1 = 0\\ \Leftrightarrow {\left( {z + \overline z } \right)^2} + {\left| z \right|^4} - 6{\left| z \right|^2} + 1 = 0\\ \Leftrightarrow {\left| z \right|^4} - 6{\left| z \right|^2} + 1 = - {\left( {z + \overline z } \right)^2} \le 0\\ \Leftrightarrow 3 - 2\sqrt 2 \le {\left| z \right|^2} \le 3 + 2\sqrt 2 \\ \Leftrightarrow \sqrt 2 - 1 \le \left| z \right| \le \sqrt 2 + 1 \Rightarrow \left\{ \begin{array}{l} \left| {{z_1}} \right| = \sqrt 2 - 1\\ \left| {{z_2}} \right| = \sqrt 2 + 1 \end{array} \right. \end{array}
Dấu = xảy ra
\Leftrightarrow \left\{ \begin{array}{l} \left| {{z_1}} \right| = \sqrt 2 - 1\\ \left| {{z_2}} \right| = \sqrt 2 + 1\\ z + \overline z = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left[ \begin{array}{l} {z_1} = \left( {\sqrt 2 - 1} \right)i\\ {z_1} = \left( {1 - \sqrt 2 } \right)i \end{array} \right.\\ \left[ \begin{array}{l} {z_2} = \left( {\sqrt 2 + 1} \right)i\\ {z_2} = \left( { - \sqrt 2 - 1} \right)i \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \left| w \right| = \left| {{z_1} + {z_2}} \right| = 2\sqrt 2 \\ \left| w \right| = \left| {{z_1} + {z_2}} \right| = 2 \end{array} \right.
Cho hai số phức {{z}_{1}};{{z}_{2}} thỏa mãn điều kiện 2\left| \overline{{{z}_{1}}}+i \right|=\left| \overline{{{z}_{1}}}-{{z}_{1}}-2i \right| và \left| {{z}_{2}}-i-10 \right|=1. Tìm giá trị nhỏ nhất của biểu thức \left| {{z}_{1}}-{{z}_{2}} \right| ?
Gọi {{z}_{1}}=x+yi ta có:
2\left| x-yi+i \right|=\left| x-yi-x-yi-2i \right| \Leftrightarrow 2\left| x-yi+i \right|=2\left| yi+i \right| \Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( y+1 \right)}^{2}} \Leftrightarrow {{x}^{2}}+{{y}^{2}}-2y+1={{y}^{2}}+2y+1 \Leftrightarrow {{x}^{2}}=4y \Leftrightarrow y=\dfrac{{{x}^{2}}}{4}
\Rightarrow Tập hợp các điểm biểu diễn cho số phức {{z}_{1}} là parabol y=\dfrac{{{x}^{2}}}{4}.
Tập hợp các điểm biểu diễn cho số phức {{z}_{2}} là là đường tròn \left( C \right) tâm I\left( 10;1 \right) bán kính R=1.
\Rightarrow \left( C \right):\,\,{{\left( x-10 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1.
Gọi M, N lần lượt là điểm biểu diễn cho số phức {{z}_{1}},{{z}_{2}}\Rightarrow \left| {{z}_{1}}-{{z}_{2}} \right|=\left| \overrightarrow{OM}-\overrightarrow{ON} \right|=MN
\Rightarrow {{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}\Leftrightarrow M{{N}_{\min }}.
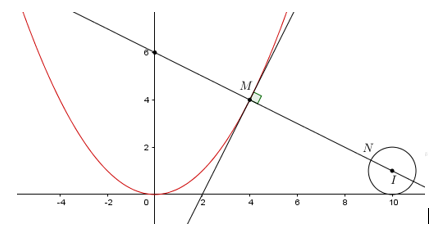
Dựa vào hình vẽ ta thấy M{{N}_{\min }}\Leftrightarrow MN\bot tiếp tuyến tại M của parabol y=\dfrac{{{x}^{2}}}{4} và đi qua I.
Ta có y'=\dfrac{x}{2} . Gọi M\left( m;\dfrac{{{m}^{2}}}{4} \right)\,\,\left( m>0 \right)\Rightarrow y'\left( m \right)=\dfrac{m}{2}\Rightarrow pttt:\,\,y=\left( x-m \right)+\dfrac{{{m}^{2}}}{4}=\dfrac{m}{2}x-\dfrac{{{m}^{2}}}{4}\,\,\left( d \right)
\begin{align} \Rightarrow MN\ge d\left( I;d \right)-1\Rightarrow M{{N}_{\min }}\Leftrightarrow d\left( I;d \right)=IM \\ \Leftrightarrow \dfrac{\left| 5m-1-\dfrac{{{m}^{2}}}{4} \right|}{\sqrt{1+\dfrac{{{m}^{2}}}{4}}}=\sqrt{{{\left( m-10 \right)}^{2}}+{{\left( \dfrac{{{m}^{2}}}{4}-1 \right)}^{2}}} \\ \Leftrightarrow \dfrac{{{\left( 5m-1-\dfrac{{{m}^{2}}}{4} \right)}^{2}}}{1+\dfrac{{{m}^{2}}}{4}}={{\left( m-10 \right)}^{2}}+{{\left( \dfrac{{{m}^{2}}}{4}-1 \right)}^{2}} \\ \end{align}
Giải phương trình trên ra tìm được m=4, khi đó IM=3\sqrt{5}\Rightarrow M{{N}_{\min }}=3\sqrt{5}-1 .
Cho hai số phức {{z}_{1}},\,\,{{z}_{2}} thỏa mãn \left| {{z}_{1}}-3i+5 \right|=2 và \left| i{{z}_{2}}-1+2i \right|=4. Tìm giá trị lớn nhất của biểu thức T=\left| 2i{{z}_{1}}+3{{z}_{2}} \right|.
Ta có \left| {{z}_{1}}-3i+5 \right|=2\Leftrightarrow \left| 2i\left( {{z}_{1}}-3i+5 \right) \right|=2.\left| 2i \right|\Leftrightarrow \left| 2i{{z}_{1}}+6+10i \right|=4.Và \left| i{{z}_{2}}-1+2i \right|=4\Leftrightarrow \left| {{z}_{2}}-\frac{1-2i}{i} \right|=4\Leftrightarrow \left| {{z}_{2}}+2+i \right|=4\Leftrightarrow \left| -\,3{{z}_{2}}-6-3i \right|=12.Đặt \left\{ \begin{array}{l} u = 2i{z_1}\\ v = - \,3{z_2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \left| {u + 6 + 10i} \right| = 4\\ \left| {v - 6 - 3i} \right| = 12 \end{array} \right. và T=\left| 2i{{z}_{1}}+3{{z}_{2}} \right|=\left| 2i{{z}_{1}}-\left( -\,3{{z}_{2}} \right) \right|=\left| u-v \right|.Tập hợp điểm M biểu diễn số phức u là đường tròn {{\left( x+6 \right)}^{2}}+{{\left( y+10 \right)}^{2}}=16 tâm {{I}_{1}}\left( -\,6;-\,10 \right),\,\,{{R}_{1}}=4.Tập hợp điểm N biểu diễn số phức v là đường tròn {{\left( x-6 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=144 tâm {{I}_{2}}\left( 6;3 \right),\,\,{{R}_{2}}=12.Khi đó T=M{{N}_{\max }}\,\Leftrightarrow \,\,MN={{I}_{1}}{{I}_{2}}+{{R}_{1}}+{{R}_{2}}=\sqrt{{{12}^{2}}+{{13}^{2}}}+4+12=\sqrt{313}+16.

