Cho số phức z thỏa mãn điều kiện \(\left| z-1 \right|=\sqrt{2}\). Tìm giá trị lớn nhất của biểu thức

\(T=\left| z+i \right|+\left| z-2-i \right|\)

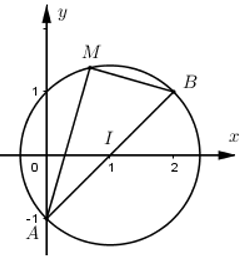
Tập hợp các điểm z thỏa mãn điều kiện \(\left| z-1 \right|=\sqrt{2}\) là đường tròn \(\left( C \right)\) tâm \(I\left( 1;0 \right)\) bán kính \(R=\sqrt{2}\).

\(T=\left| z+i \right|+\left| z-2-i \right|=\left| z-\left( -1 \right) \right|+\left| z-\left( 2+i \right) \right|\)

Gọi M là điểm biểu diễn cho số phức z, \(A\left( 0;-1 \right)\) là điểm biểu diễn cho số phức \(-i\), \(B\left( 2;1 \right)\) là điểm biểu diễn cho số phức \(2+i\). Dễ thấy \(A,B\in \left( C \right)\) và \(AB=\sqrt{{{2}^{2}}+{{2}^{2}}}=2\sqrt{2}=2R\Rightarrow AB\) là đường kính của đường tròn \(\left( C \right)\Rightarrow \Delta MAB\) vuông tại M \(\Rightarrow M{{A}^{2}}+M{{B}^{2}}=A{{B}^{2}}=8\Rightarrow MB=\sqrt{8-M{{A}^{2}}}\)

Ta có: \(T=\left| \overrightarrow{OM}-\overrightarrow{OA} \right|+\left| \overrightarrow{OM}-\overrightarrow{OB} \right|=MA+MB=MA+\sqrt{8-M{{A}^{2}}}\)

Đặt \(MA=x\,\,\left( 0\le x\le 2\sqrt{2} \right)\), xét hàm số \(f\left( x \right)=x+\sqrt{8-{{x}^{2}}}\) trên \(\left[ 0;2\sqrt{2} \right]\) ta có:

\(f'\left( x \right)=1-\frac{x}{\sqrt{8-{{x}^{2}}}}=\frac{\sqrt{8-{{x}^{2}}}-x}{\sqrt{8-{{x}^{2}}}}=0\Leftrightarrow \sqrt{8-{{x}^{2}}}=x\Leftrightarrow 8-{{x}^{2}}={{x}^{2}}\Leftrightarrow x=2\)

\(\begin{align}  & f\left( 0 \right)=\sqrt{2},\,\,f\left( 2\sqrt{2} \right)=2\sqrt{2};\,\,f\left( 2 \right)=4 \\  & \Rightarrow \underset{\left[ 0;2\sqrt{2} \right]}{\mathop{\max }}\,f\left( x \right)=f\left( 2 \right)=4 \\ \end{align}\)

Vậy \(\max T=4\).