Tìm điểm M biểu diễn số phức z=i−2
z=i−2=−2+i nên điểm biểu diễn là M(−2;1)
Cho số phức z thỏa mãn (1+i)z=3−i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình bên ?

(1+i)z=3−i⇒z=3−i1+i=(3−i)(1−i)(1+i)(1−i)=2−4i12+12=1−2i⇒Q(1;−2) là điểm biểu diễn z.
Trên mặt phẳng tọa độ, cho hai số phức z1=2+i và z2=1−i. Điểm biểu diễn số phức z1−z2 là điểm nào dưới đây?
Ta có: {z1=2+iz2=1−i ⇒z1−z2=(2−1)+(1+1)i=1+2i
⇒N(1;2) là điểm biểu diễn số phức z1−z2.
Trong hình bên .M,N. lần lượt là điểm biểu diễn số phức z và w. Số phức z+w bằng?

Dựa vào hình vẽ ta thấy: M(−1;2)⇒z=−1+2i và N(2;1)⇒w=2+i.
Khi đó ta có: z+w=−1+2i+2+i=1+3i.
Cho ba số phức z1=4−3i, z2=(1+2i)i và z3=1−i1+i có điểm biểu diễn trên mặt phẳng Oxylần lượt là A, B, C. Số phức nào dưới đây có điểm biểu diễn là điểm D thỏa ABCD là hình bình hành?
Ta có
z1=4−3i⇒A(4;−3)
z2=(1+2i)i=−2+i⇒B(−2;1)
z3=1−i1+i=−i⇒C(0;−1)
Vì ABCD là hình bình hành nên →AB=→DC.
⇔{−2−4=0−xD1−(−3)=−1−yD⇔{xD=6yD=−5.
Vậy số phức có điểm biểu diễn là điểm D(6;−5) có dạng z=6−5i.
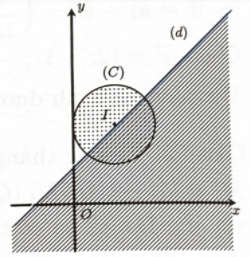
Cho số phức z thỏa mãn {|z−1−2i|≤1|z−1+2i|≥|z+3−2i|. Gọi S là diện tích phần mặt phẳng chứa các điểm biểu diễn của số phức z. Tính S.
Bước 1: Giả sử z=x+yi(x,y∈R). Giải |z−1−2i|≤1
Giả sử z=x+yi(x,y∈R). Khi đó
|z−1−2i|≤1 ⇔|(x−1)+(y−2)i|≤1⇔√(x−1)2+(y−2)2≤1⇔(x−1)2+(y−2)2≤1
Bước 2: Giải |z−1+2i|≥|z+3−2i|
Và |z−1+2i|≥|z+3−2i| ⇔√(x−1)2+(y+2)2≥√(x+3)2+(y−2)2
⇔(x−1)2+(y+2)2≥(x+3)2+(y−2)2⇔y≥x+1
Bước 3: Gọi (T) là nửa mặt phẳng có bờ là đường thẳng d:y=x+1, không chứa gốc tọa độ O(0;0). Tính S.
Gọi (T) là nửa mặt phẳng có bờ là đường thẳng d:y=x+1, không chứa gốc tọa độ O(0;0). Khi đó tập hợp các điểm biểu diễn số phức z thỏa mãn đề là nửa hình tròn (C) tâm I(1;2), bán kính R=1 và thuộc (T). Vì đường thẳng d đi qua tâm I(1;2) của hình tròn (C) nên diện tích cần tìm là một nửa diện tích hình tròn (C). Do đó S=π2.
Có bao nhiêu số phức z thỏa mãn |z+2−i|=2√2 và (z−i)2 là một số thực?
Đặt z=a+bi
Ta có |z+2−i|=2√2⇒(a+2)2+(b−1)2=8 (*)
Mặt khác (z−i)2=(a+bi−i)2=a2−(b−1)2+2a(b−1)i là một số thực nên 2a(b−1)=0 ⇔[a=0b−1=0⇔[a=0b=1
Với a=0, (*) trở thành:
(b−1)2=4⇔[b=3b=−1⇒[z=3iz=−i
Với b=1, (*) trở thành:
(a+2)2=8⇔[a=−2+2√2a=−2−2√2⇒[z=−2+2√2+iz=−2−2√2+i
Vậy có 4 số phức z thỏa mãn yêu cầu bài toán.
Đề thi THPT QG - 2021 - mã 103
Trên mặt phẳng tọa độ, điểm M(−2;3) là điểm biểu diễn của số phức nào dưới đây?
Điểm M(−2;3) là điểm biểu diễn của số phức z1=−2+3i.
Trong mặt phẳng tọa độ, cho A,B,C là ba điểm biểu diễn lần lượt cho ba số phức z1=5−i, z2=(4+i)2 và z3=(2i)3. Diện tích của tam giác ABC là kết quả nào dưới đây?
Ta có:
z1=5−i⇒A(5;−1).
z2=(4+i)2=15+8i⇒B(15;8).
z3=(2i)3=−8i⇒C(0;−8).
Ta có
AB=√102+92=√181AC=√(−5)2+(−7)2=√74BC=√(−15)2+(−16)2=√481
Gọi p là nửa chu vi tam giác ABC ta có: p=AB+AC+BC2=√181+√74+√4812.
Vậy diện tích tam giác ABC là: S=√p(p−AB)(p−AC)(p−BC)=252.
Điểm biểu diễn số phức z=2−3i có tọa độ là:
Gọi A là điểm biểu diễn số phức, suy ra {xA=2yA=−3.
Vậy A(2;−3).
Trong mặt phẳng tọa độ (hình vẽ bên), số phức z=3−4i được biểu diễn bởi điểm nào trong các điểm A,B,C,D?
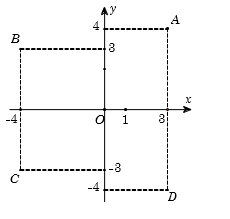
Số phức z=3−4i biểu diễn điểm có tọa độ là (3;−4), đây chính là điểm D.
Giả sử M,N,P,Q được cho ở hình vẽ bên là điểm biểu diễn của các số phức z1,z2,z3,z4 trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
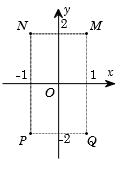
Dựa vào hình vẽ ta thấy
Điểm M là điểm biểu diễn số phức z1=1+2i.
Điểm Q là điểm biểu diễn số phức z4=1−2i.
Điểm N là điểm biểu diễn số phức z2=−1+2i.
Điểm P là điểm biểu diễn số phức z3=−1−2i.
Cho số phức z=2+5i. Tìm số phức w=iz+¯z.
¯z=2−5i⇒w=i(2+5i)+2−5i=−3−3i.
Cho số phức z thỏa mãn (1−i)z+2iˉz=5+3i. Tìm số phức w=z+2ˉz.
Đặt z=a+bi(a;b∈R), suy ra ˉz=a−bi.
Theo giả thiết, ta có (1−i)(a+bi)+2i(a−bi)=5+3i⇔(a+3b−5)+(a+b−3)i=0
⇔{a+3b−5=0a+b−3=0⇔{a=2b=1 ⇒z=2+i⇒ˉz=2−i
Vậy w=z+2ˉz=(2+i)+2(2−i)=6−i.
Gọi S là tổng phần thực và phần ảo của số phức w=z3−i, biết z thỏa mãn z+2−4i=(2−i)¯iz. Mệnh đề nào sau đây đúng?
Đặt z=x+yi(x;y∈R), suy ra iz=i(x+yi)=−y+xi ⇒¯iz=−y−xi
Theo giả thiết, ta có x+yi+2−4i=(2−i)(−y−xi)
⇔x+2+(y−4)i=(−2y−x)+(y−2x)i ⇔{x+2=−2y−xy−4=y−2x⇔{x=2y=−3⇒z=2−3i
Khi đó w=z3−i=(2−3i)3−i=−46−10i.
Cho số phức z=z21+|z1|2 với z1 là số thuần ảo. Mệnh đề nào sau đây đúng?
Gọi z1=m.i(m∈R)⇒{z21=(m.i)2=m2.i2=−m2|z1|=√02+m2=|m|⇒|z1|2=m2.
Khi đó z=z21+|z1|2=−m2+m2=0.
Đề thi THPT QG 2019 – mã đề 104
Cho hai số phức z1=2−i và z2=1+i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 2z1+z2 có tọa độ là
2z1+z2=2(2−i)+1+i=4−2i+1+i=5−i.
Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 2z1+z2 có tọa độ là (5;−1).
Cho số phức z thỏa mãn 1−iz+1=1+i. Điểm M biểu diễn của số phức w=z3+1 trên mặt phẳng tọa độ có tọa độ là:
Ta có 1−iz+1=1+i⇔z+1=1−i1+i ⇔z+1=−i⇒z=−1−i
Suy ra w=z3+1=(−1−i)3+1=−(1+i)3+1=3−2i
⇒M(3;−2)
Cho số phức z thỏa mãn |z|=1 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w=1z là một trong bốn điểm M,N,P,Q. Khi đó điểm biểu diễn của số phức w là
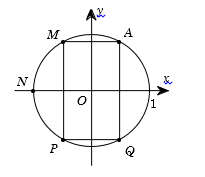
Gọi z=x+yi(x;y∈R) được biểu diễn bởi A.
Từ giả thiết, ta có {x2+y2=1x>0;y>0.
Ta có w=1z=1x+yi=x−yix2+y2=x−yi=ˉz.
Vì hai số phức z và ˉz có điểm biểu diễn đối xứng qua trục hoành nên ta chọn điểm Q thỏa mãn yêu cầu bài toán.
Xét các số phức z thỏa mãn |z+2+i|=|¯z+i|. Tập hợp điểm biểu diễn các số phức z là đường thẳng có phương trình
Gọi z=x+yi(x,y∈R), khi đó ta có:
|x+yi+2+i|=|x−yi+i|⇔(x+2)2+(y+1)2=x2+(y−1)2⇔4x+4+2y+1=−2y+1⇔4x+4y+4=0⇔x+y+1=0
Vậy tập hợp điểm biểu diễn số phức z là đường thẳng có phương trình x+y+1=0.

