Các bài toán về mặt cầu và mặt phẳng

Mặt cầu \(\left( S \right)\) có tâm là \(I\left( {1;2;0} \right)\) và bán kính là \(R = 3\) \( \Rightarrow {d_{\left( {I,\left( Q \right)} \right)}} = \dfrac{2}{{\sqrt 3 }} < R\)

\( \Rightarrow \) Mặt cầu \(\left( S \right)\) cắt \(\left( Q \right)\) và tâm \(I\) không thuộc mặt phẳng \(\left( Q \right)\).

Ta có hình vẽ minh họa như sau:

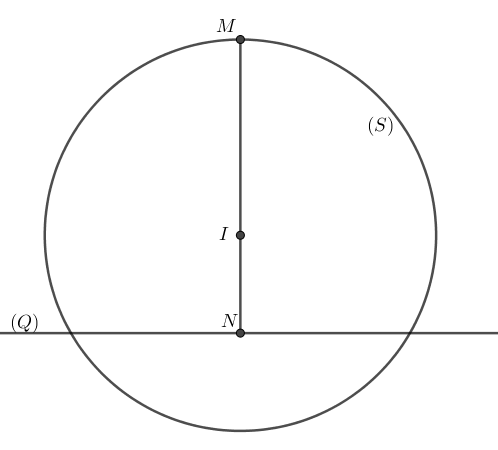
Vẽ hình, ta xác định được độ dài \(MN\) lớn nhất đồng thời vuông góc với mặt phẳng \(\left( Q \right)\) như hình vẽ trên.

\( \Rightarrow \) \(I,M,N\) thẳng hàng.

Khi đó, \(MN:\left\{ \begin{array}{l}\overrightarrow u  = \overrightarrow {{n_{\left( Q \right)}}}  = \left( {1; - 1;1} \right)\\I\left( {1;2;0} \right) \in MN\end{array} \right.\) \( \Rightarrow MN:\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{{ - 1}} = \dfrac{z}{1}\).

\( \Rightarrow \left\{ \begin{array}{l}M\left( {1 + t;2 - t;t} \right) \in \left( S \right)\\N\left( {1 + u;2 - u;u} \right) \in \left( Q \right)\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}{\left( {1 + t - 1} \right)^2} + {\left( {2 - t - 2} \right)^2} + {t^2} = 9\\1 + u - \left( {2 - u} \right) + u - 1 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}t = \sqrt 3 \\t =  - \sqrt 3 \end{array} \right.\\u = \dfrac{2}{3}\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}N\left( {\dfrac{5}{3};\dfrac{4}{3};\dfrac{2}{3}} \right)\\{M_1}\left( {1 + \sqrt 3 ;2 - \sqrt 3 ;\sqrt 3 } \right)\end{array} \right.\\\left\{ \begin{array}{l}N\left( {\dfrac{5}{3};\dfrac{4}{3};\dfrac{2}{3}} \right)\\{M_2}\left( {1 - \sqrt 3 ;2 + \sqrt 3 ; - \sqrt 3 } \right)\end{array} \right.\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}\overrightarrow {{M_1}N} \left( {\dfrac{2}{3} - \sqrt 3 ;\sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} - \sqrt 3 } \right)\\\overrightarrow {{M_2}N} \left( {\dfrac{2}{3} + \sqrt 3 ; - \sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} + \sqrt 3 } \right)\end{array} \right.\)

Dễ dàng kiểm tra được \({M_2}N > {M_1}N\)

\( \Rightarrow \overrightarrow {MN}  = \overrightarrow {{M_2}N}  = \left( {\dfrac{2}{3} + \sqrt 3 ; - \sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} + \sqrt 3 } \right)\)

\(\left( S \right):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right),\,\,\,\left( {a,b,c > 0} \right),\,\,R = \sqrt {{a^2} + {b^2} + {c^2} - d} ,\,\,\left( {{a^2} + {b^2} + {c^2} > d} \right)\)

\(\begin{array}{l}M\left( {2;0;1} \right) \in \left( S \right) \Rightarrow {2^2} + {0^2} + {1^2} - 2a.2 - 2b.0 - 2c.1 + d = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 4a + 2c - d = 5 \Leftrightarrow d = 4a + 2c - 5\end{array}\)

Khi đó: \(R = \sqrt {{a^2} + {b^2} + {c^2} - d}  = \sqrt {{a^2} + {b^2} + {c^2} - 4a - 2c + 5} \)

\(r_1^2 = {R^2} - {d^2}\left( {I;\left( {Oxy} \right)} \right) = {a^2} + {b^2} + {c^2} - 4a - 2c + 5 - {c^2}\)

\( \Rightarrow {a^2} + {b^2} - 4a - 2c + 5 = 13\)

\(\left( S \right)\) cắt 3 mặt phẳng tọa độ \(\left( {Oxy} \right),\left( {Oxz} \right),\left( {Oyz} \right)\) theo các giao tuyến là các đường tròn có bán kính bằng \(\sqrt {13} \) \(\begin{array}{l} \Rightarrow {a^2} + {b^2} = {b^2} + {c^2} = {c^2} + {a^2} = 13 \Rightarrow {a^2} = {b^2} = {c^2} \Leftrightarrow a = b = c > 0\\ \Rightarrow {a^2} + {b^2} - 4a - 2c + 5 = 13 \Leftrightarrow 2{a^2} - 6a - 8 = 0 \Leftrightarrow \left[ \begin{array}{l}a = 4\\a =  - 1\,\,\,\left( {ktm} \right)\end{array} \right.\\ \Rightarrow a = b = c = 4 \Rightarrow a + b + c = 12.\end{array}\)  

Gọi E là hình chiếu của I trên Oy $ \Rightarrow E\left( {0; - 2;0} \right)$

Suy ra bán kính mặt cầu tâm I và tiếp xúc với trục Oy là: $R = IE = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( { - 2 + 2} \right)}^2} + {{\left( {3 - 0} \right)}^2}}  = \sqrt {10} $

Vậy phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:$\;{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 10.$

Gọi mặt phẳng $\left( P \right)$ là mặt phẳng cần tìm.$\left( P \right)//\left( {\alpha {\rm{\;}}} \right) \Rightarrow $ Phương trình mặt phẳng $\left( P \right)$ có dạng $4x + 3y - 12z + D = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {D \ne 10} \right)$

Mặt cầu $\left( S \right)$ có tâm $I\left( {1;2;3} \right)$, bán kính $R = 4$.

$\left( P \right)$ tiếp xúc với $\left( S \right) \Rightarrow d\left( {I;\left( P \right)} \right) = R$$ \Rightarrow \dfrac{{\left| {4.1 + 3.2 - 12.3 + D} \right|}}{{\sqrt {{4^2} + {3^2} + {{\left( { - 12} \right)}^2}} }} = 4 \Leftrightarrow \left| {D - 26} \right| = 52 \Leftrightarrow \left[ \begin{array}{l}D = 78\\D =  - 26\end{array} \right.$

Vậy mặt phẳng $\left( P \right)$ thỏa mãn yêu cầu bài toán có phương trình  $\left[ \begin{array}{l}4x + 3y - 12z - 26 = 0\\4x + 3y - 12z + 78 = 0\end{array} \right.$

Mặt cầu (S) có tâm \(I\left( 1;1;-2 \right)\) và bán kính \(R=\sqrt{7}\).

Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính lớn nhất thì \(d\left( I;\left( P \right) \right)\) nhỏ nhất.

Ta có \(d\left( I;\left( P \right) \right)=\frac{\left| 1+1-\left( -2 \right)-m \right|}{\sqrt{3}}=\frac{\left| 4-m \right|}{\sqrt{3}}\)

\(\Rightarrow d{{\left( I;\left( P \right) \right)}_{\min }}=0\Leftrightarrow m=4\)

Mặt cầu (S) có tâm \(I\left( 1;2;0 \right)\), bán kính R = 5.

\(d\left( I;\left( \alpha  \right) \right)=\frac{\left| 1+2.2+7 \right|}{\sqrt{1+4+4}}=4=d\).

Do đó mặt phẳng \(\left( \alpha  \right):\,\,x+2y-2z+7=0\) cắt nhau theo một đường tròn (C) có bán kính \(r=\sqrt{{{R}^{2}}-{{d}^{2}}}=3\).

Vậy chu vi đường tròn (C) bằng \(2\pi r=6\pi \).

Mặt phẳng \(\left( \beta  \right)\) cắt mặt cầu \(\left( S \right)\) theo đường tròn có bán kính \(r=\frac{8\pi }{2\pi }=4\).

Mặt cầu \(\left( S \right)\) có tâm \(I\left( -1;2;3 \right)\), bán kính \(R=\sqrt{17-m}\).

Ta có \(d\left( I;\left( \beta  \right) \right)=\frac{\left| -2-2+6-8 \right|}{\sqrt{4+1+4}}=2=d\)

Áp dụng định lí Pytago ta có \({{R}^{2}}={{r}^{2}}+{{d}^{2}}={{2}^{2}}+{{4}^{2}}=20\Leftrightarrow 17-m=20\Leftrightarrow m=-3\).

Xét mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=9\) có tâm \(I\left( 1;2;2 \right),\) bán kính \(R=3.\)

Khoảng cách từ tâm \(I\,\,\xrightarrow{{}}\,\,mp\,\,\left( P \right)\) là \(d\left( I;\left( P \right) \right)=\frac{\left| 2.1-1.2-2.2+1 \right|}{\sqrt{{{2}^{2}}+{{\left( -\,1 \right)}^{2}}+{{2}^{2}}}}=1.\)

Vậy bán kính đường tròn giao tuyến là \(r=\sqrt{{{R}^{2}}-{{d}^{2}}\left( I;\left( P \right) \right)}=2\sqrt{2}.\)

Mặt cầu \(\left( S \right):\,\,\,{x^2} + {y^2} + {z^2} - 2x - 4y - 4z = 0\) có tâm \(I\left( {1;2;2} \right)\), bán kính \(R = \sqrt {{1^2} + {2^2} + {3^2} - 0}  = \sqrt {14} \).

Gọi \(\left( P \right)\) là mặt phẳng tiếp xúc với mặt cầu \(\left( S \right)\) tại \(A\left( {3;4;3} \right)\), khi đó ta có \(IA \bot \left( P \right)\) nên \(\left( P \right)\) nhận \(\overrightarrow {IA}  = \left( {2;2;1} \right)\) là 1 VTPT.

Vậy phương trình mặt phẳng \(\left( P \right)\) đi qua \(A\left( {3;4;3} \right)\) và có 1 VTPT \(\overrightarrow {IA}  = \left( {2;2;1} \right)\) là:

\(2\left( {x - 3} \right) + 2\left( {y - 4} \right) + 1\left( {z - 3} \right) = 0\) \( \Leftrightarrow 2x + 2y + z - 17 = 0\).

Ta có \(d\left( I;\left( P \right) \right)=\frac{\left| -1-2.2-2.1-2 \right|}{\sqrt{1+4+4}}=3=R\).

Vậy phương trình mặt cầu là: \(\left( S \right):\,\,{{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9\)

Vì \(I\) thuộc tia \(Ox\)\(\Rightarrow \) \(I\left( a;0;0 \right)\,\,\,\,\left( a>0 \right)\)\(\Rightarrow \) \(\overrightarrow{AI}=\left( a-1;2;-\,3 \right)\Rightarrow \,\,IA=\sqrt{{{\left( a-1 \right)}^{2}}+13}.\)

Mà \(A\) thuộc mặt cầu \(\left( S \right)\)\(\Rightarrow \,\,R=IA\Leftrightarrow I{{A}^{2}}=49\Leftrightarrow \,\,{{\left( a-1 \right)}^{2}}=36\Leftrightarrow \,\,a=7.\)

Vậy phương trình mặt cầu \(\left( S \right)\) là \({{\left( x-7 \right)}^{2}}+{{y}^{2}}+{{z}^{2}}=49.\)

\(\left( ABC \right):\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) \(\begin{align}  M\left( \frac{1}{7};\frac{2}{7};\frac{3}{7} \right)\in \left( ABC \right)\Rightarrow \frac{1}{7a}+\frac{2}{7b}+\frac{3}{7c}=1\Leftrightarrow \frac{1}{a}+\frac{2}{b}+\frac{3}{c}=7 \\ \end{align}\)

\(\left( ABC \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) có tâm \(I\left( 1;2;3 \right)\) và bán kính \(R=\sqrt{\frac{72}{7}}\)  

\(\begin{align}  \Rightarrow d\left( I;\left( ABC \right) \right)=R\Leftrightarrow \frac{\left| \frac{1}{a}+\frac{2}{b}+\frac{3}{c}-1 \right|}{\sqrt{\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}}}=\sqrt{\frac{72}{7}} \\  \Leftrightarrow \frac{6}{\sqrt{\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}}}=\sqrt{\frac{72}{7}}\Rightarrow \sqrt{\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}}=\frac{\sqrt{14}}{2} \\ \end{align}\)

\(\Rightarrow \frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}=\frac{7}{2}\)

Theo đề bài ta có: \(r=\sqrt{8}.\)

\(OI=d\left( I;\ \left( P \right) \right)=\frac{\left| 2.1-2+2.\left( -1 \right)-1 \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}+{{2}^{2}}}}=\frac{\left| -3 \right|}{\sqrt{9}}=1.\)

Khi đó ta có: \(R=\sqrt{O{{I}^{2}}+{{r}^{2}}}=\sqrt{1+8}=3.\)

Ta có phương trình mặt cầu cần tìm là: \({{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9.\)

Mặt cầu \(\left( S \right):\,\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\) có tâm \(I\left( {1; - 2;\,\,3} \right)\) và bán kính \(R = 5.\)

Ta có: \(\overrightarrow {IH}  = \left( {3;\,\,4;\,\,0} \right).\)

Phương trình mặt phẳng \(\left( P \right)\) cần tìm đi qua \(H\left( {4;\,\,2;\,\,3} \right)\) và tiếp xúc với mặt cầu \(\left( S \right)\) nhận \(\overrightarrow {IH} \) làm VTPT.

\( \Rightarrow \left( P \right):\,\,\,3\left( {x - 4} \right) + 4\left( {y - 2} \right) = 0\) \( \Leftrightarrow 3x + 4y - 20 = 0.\)

\(d\left( I;\left( P \right) \right)=\frac{\left| 1-2.2-2.(-1)-8 \right|}{\sqrt{{{1}^{2}}+{{2}^{2}}+{{2}^{2}}}}=3\)

\((P):x-2y-2z-8=0\) tiếp xúc với mặt cầu \(\Leftrightarrow R=d\left( I;\left( \alpha  \right) \right)=3\)

\(\Rightarrow \) Phương trình mặt cầu đó là:  \({{\left( x-1 \right)}^{2}}+{{(y-2)}^{2}}+{{(z+1)}^{2}}=9\)

Ta có: \(I\left( { - 2;\,\,5;\,\,1} \right)\) và \(\left( P \right):\,\,\,2x + 2y - z + 7 = 0\)

Mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng \(\left( P \right)\) \( \Leftrightarrow d\left( {I;\,\,\left( P \right)} \right) = R.\)

\( \Leftrightarrow R = \dfrac{{\left| {2.\left( { - 2} \right) + 2.5 - 1 + 7} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{12}}{3} = 4.\)

\( \Rightarrow \) Phương trình mặt cầu \(\left( S \right)\) cần tìm là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} + {\left( {z - 1} \right)^2} = 16.\)

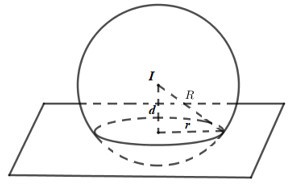
Ta có: \(d = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {2.2 + 1 + 2.1 - 1} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = \dfrac{6}{3} = 2\).

Áp dụng định lí Pytago ta có: \({R^2} = {d^2} + {r^2} = {2^2} + {4^2} = 20\) \( \Rightarrow R = 2\sqrt 5 \).

Vậy phương trình mặt cầu là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 20\).

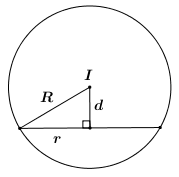
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\), bán kính \(R = \sqrt {{1^2} + {2^2} + {3^2}}  = \sqrt {14} \).

Ta có: \(d = d\left( {I;\left( {Oxy} \right)} \right) = \left| {{z_I}} \right| = 3\).

Gọi \(r\) là bán kính đường tròn giao tuyến của \(\left( S \right)\) và \(\left( {Oxy} \right)\), áp dụng định lí Pytago ta có:

\({R^2} = {r^2} + {d^2} \Leftrightarrow {r} = \sqrt {{R^2} - {d^2}}  = \sqrt {14 - 9}  = \sqrt 5 \).

Phương trình mặt phẳng \(\left( {Oxy} \right)\) là \(z = 0\) \( \Rightarrow d\left( {I;\left( {Oxy} \right)} \right) = \dfrac{{\left| { - 4} \right|}}{1} = 4\).

Vì \(\left( S \right)\) có tâm \(I\left( {1;0 - 4} \right)\) và tiếp xúc với mặt phẳng \(\left( {Oxy} \right)\) nên bán kính mặt cầu \(\left( S \right)\) là \(R = d\left( {I;\left( {Oxy} \right)} \right) = 4\).

Vậy phương trình mặt cầu \(\left( S \right)\) tâm \(I\left( {1;0 - 4} \right)\), bán kính \(R = 4\) là:

\({\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 4} \right)^2} = 16\)

Gọi \(R\) là bán kính mặt cầu cần tìm \( \Rightarrow R = d\left( {I;\,\,\left( \alpha  \right)} \right) = \dfrac{{\left| {1 - 2.2 + 2.5 + 2} \right|}}{{\sqrt {1 + {{\left( { - 2} \right)}^2} + {2^2}} }} = \dfrac{9}{3} = 3.\)

Vậy mặt cầu tâm \(I\) và tiếp xúc với \(\left( \alpha  \right)\) có phương trình  là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 9.\)