Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình \(f\left( {\sin x} \right) = m\) có nghiệm thuộc khoảng \(\left( {0;\pi } \right)\) là
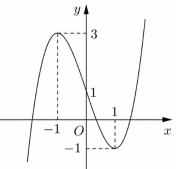
Đặt \(\sin x = t\). Với \(x \in \left( {0;\pi } \right) \Rightarrow t \in \left( {0;1} \right]\).
Khi đó phương trình ban đầu trở thành \(f\left( t \right) = m\) có nghiệm \(t \in \left( {0;1} \right]\).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và \(y = m\).
Dựa vào đồ thị hàm số ta thấy, để phương trình \(f\left( t \right) = m\) có nghiệm \(t \in \left( {0;1} \right]\)\( \Rightarrow m \in \left[ { - 1;1} \right)\).
Cho các số thực dương \(x\), \(y\). Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{{4x{y^2}}}{{{{\left( {x + \sqrt {{x^2} + 4{y^2}} } \right)}^3}}}\)
\(P = \dfrac{{4x{y^2}}}{{{{\left( {x + \sqrt {{x^2} + 4{y^2}} } \right)}^3}}} = \dfrac{{4{{\left( {\dfrac{y}{x}} \right)}^2}}}{{{{\left( {1 + \sqrt {1 + 4{{\left( {\dfrac{y}{x}} \right)}^2}} } \right)}^3}}}\) \(\left( {\forall x >0,y > 0} \right)\)
Đặt \(t = \sqrt {1 + 4{{\left( {\dfrac{y}{x}} \right)}^2}} \), \(t > 1\). Khi đó biểu thức trở thành \(P\left( t \right) = \dfrac{{{t^2} - 1}}{{{{\left( {t + 1} \right)}^3}}}=\dfrac{{t - 1}}{{{{\left( {t + 1} \right)}^2}}}\) với \(t > 1\)
\(P'\left( t \right) = \dfrac{{ - {t^2} + 2t + 3}}{{{{\left( {t + 1} \right)}^4}}} = 0 \Leftrightarrow t = 3\)
Bảng biến thiên:
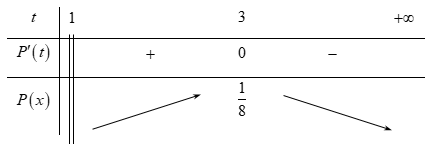
Vậy $\max P = P\left( 3 \right) = \dfrac{1}{8}$.
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) cắt trục \(Ox\) tại ba điểm có hoành độ \(a < b < c\) như hình vẽ.
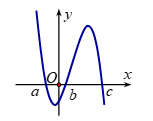
Khẳng định nào dưới đây có thể xảy ra?
Dùng bảng biến thiên kết hợp các phương án để loại trừ.
Từ đồ thị của \(y = f'\left( x \right)\) ta có bảng biến thiên như sau
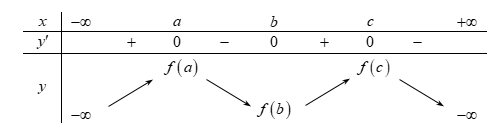
Từ bảng biến thiên ta có \(f\left( a \right) > f\left( b \right),f\left( c \right) > f\left( b \right)\) (\(f\left( b \right)\) là số nhỏ nhất) nên phương án C có thể xảy ra.
Một sợi dây có chiều dài là \(6\,\,{\rm{m}}\), được chia thành hai phần. Phần thứ nhất được uốn thành hình tam giác đều, phần thứ hai uốn thành hình vuông. Hỏi độ dài của cạnh hình tam giác đều bằng bao nhiêu để diện tích hai hình thu được là nhỏ nhất?
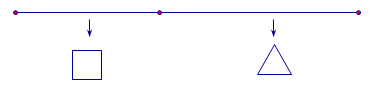
Gọi cạnh tam giác đều là $x$ khi đó chu vi tam giác đều là $3x$ và chu vi hình vuông là \(6 - 3x\)
Cạnh hình vuông có độ dài là \(\dfrac{{6 - 3x}}{4},\)\(\left( {0 < x < 2} \right)\)
Tổng diện tích hình tam giác đều và hình vuông là
\(S = \dfrac{{{x^2}\sqrt 3 }}{4} + {\left( {\dfrac{{6 - 3x}}{4}} \right)^2} = \dfrac{{\left( {4\sqrt 3 + 9} \right){x^2} - 36x + 36}}{{16}} = f\left( x \right)\)
Khảo sát hàm số \(f\left( x \right)\) trên \(\left( {0 < x < 2} \right)\) ta thấy \({S_{\min }} \Leftrightarrow x = \dfrac{{18}}{{4\sqrt 3 + 9}}.\)
Cho \(x\), \(y\) là các số thực thỏa mãn \(x + y = \sqrt {x - 1} + \sqrt {2y + 2} \). Gọi \(M\), \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của \(P = {x^2} + {y^2} + 2\left( {x + 1} \right)\left( {y + 1} \right) + 8\sqrt {4 - x - y} \). Tình giá trị \(M + m\).
Đk: \(x \ge 1;y \ge - 1\). Đặt \(t = x + y\); \(t \ge 0\).
Có \(\sqrt {x - 1} + \sqrt {2y + 2} = \sqrt {x - 1} + \sqrt 2 .\sqrt {y + 1} \le \sqrt {3\left( {x + y} \right)} \Rightarrow x + y \le \sqrt {3\left( {x + y} \right)} \).
Vậy \(t \le \sqrt {3t} \Leftrightarrow {t^2} - 3t \le 0 \Leftrightarrow 0 \le t \le 3\).
\(P = {\left( {x + y} \right)^2} + 2\left( {x + y} \right) + 2 + 8\sqrt {4 - \left( {x + y} \right)} \) nên \(P = {t^2} + 2t + 2 + 8\sqrt {4 - t} \)
\(P' = 2t + 2 - \dfrac{4}{{\sqrt {4 - t} }}\)
\(P' = 0 \Leftrightarrow \left( {2t + 2} \right)\sqrt {4 - t} = 4\) \( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 1 \pm 2\sqrt 2 \notin \left[ {0;3} \right]\end{array} \right.\).
\(P\left( 0 \right) = 18;\)\(P\left( 3 \right) = 25\).
Suy ra $M = 25;m = 18$\( \Rightarrow M + m = 43\).
Tìm \(m\) để hàm số \(y = \dfrac{{2\cot x + 1}}{{\cot x + m}}\) đồng biến trên khoảng \(\left( {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right)\)?
Đặt \(t = \cot x\), \(x \in \left[ {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right]\) \( \Rightarrow t \in \left( {0;1} \right)\).
Xét hàm số \(f\left( t \right) = \dfrac{{2t + 1}}{{t + m}}\) trên khoảng \(\left( {0;\,\,1} \right)\),\(t \ne - m\).
Ta có \(f'\left( t \right) = \dfrac{{2m - 1}}{{{{\left( {t + m} \right)}^2}}}\), \(\forall t \in \left( {0;1} \right)\),\(t \ne - m\).
Khi đó để hàm số đã cho đồng biến trên khoảng \(\left( {\dfrac{\pi }{4};\,\,\dfrac{\pi }{2}} \right)\) thì \(f\left( t \right)\) nghịch biến trên khoảng \(\left( {0;\,\,1} \right)\) (vì \(t' = \dfrac{{ - 1}}{{{{\sin }^2}x}} < 0,\,\)\(\forall x \in \left( {\dfrac{\pi }{4};\,\,\dfrac{\pi }{2}} \right)\) \( \Leftrightarrow f'\left( t \right) < 0,\)\(\forall t \in \left( {0;\,\,1} \right)\),\(t \ne - m\)).
Điều kiện: \(\left\{ \begin{array}{l}2m - 1 < 0\\ - m \notin \left( {0;\,1} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{1}{2}\\\left[ \begin{array}{l} - m \le 0\\ - m \ge 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{1}{2}\\\left[ \begin{array}{l}m \ge 0\\m \le - 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m \le - 1\\0 \le m < \dfrac{1}{2}\end{array} \right.\).
Hàm số \(f\left( x \right) = \left| {8{x^4} - 8{x^2} + 1} \right|\) đạt giá trị lớn nhất trên đoạn \(\left[ { - 1;\,\,1} \right]\) tại bao nhiêu giá trị của \(x\)?
Xét hàm số \(f\left( x \right) = \left| {8{x^4} - 8{x^2} + 1} \right| = \sqrt {{{\left( {8{x^4} - 8{x^2} + 1} \right)}^2}} \) trên đoạn \(\left[ { - 1;\,\,1} \right]\).
Ta có \(f'\left( x \right) = \dfrac{{\left( {32{x^3} - 16x} \right)\left( {8{x^4} - 8{x^2} + 1} \right)}}{{\sqrt {{{\left( {8{x^4} - 8{x^2} + 1} \right)}^2}} }}\)
\(f'\left( x \right) = 0 \Leftrightarrow {32{x^3} - 16x} = 0\) \(\Leftrightarrow x = 0;\,\,x = \pm \dfrac{1}{{\sqrt 2 }}\)
$8{x^4} - 8{x^2} + 1\ne 0$\( \Leftrightarrow x \ne \pm \dfrac{{\sqrt {2 + \sqrt 2 } }}{2};\,\,x \ne \pm \dfrac{{\sqrt {2 - \sqrt 2 } }}{2}\)
Mà \(f\left( 0 \right) = 1\); \(f\left( { \pm \dfrac{1}{{\sqrt 2 }}} \right) = 1\); \(f\left( { \pm \dfrac{{\sqrt {2 + \sqrt 2 } }}{2}} \right) = 0\); \(f\left( { \pm \dfrac{{\sqrt {2 - \sqrt 2 } }}{2}} \right) = 0\),\(f\left( { \pm 1} \right) = 1\)
Vậy \(\mathop {\max }\limits_{\left[ { - 1;\,1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( { \pm \dfrac{1}{{\sqrt 2 }}} \right) = f\left( { \pm 1} \right) = 1\)
Cho \(x\), \(y\) là những số thực thoả mãn \({x^2} - xy + {y^2} = 1\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(P = \dfrac{{{x^4} + {y^4} + 1}}{{{x^2} + {y^2} + 1}}\). Giá trị của \(A = M + 15m\) là
Ta có
+) \(1 + xy = {x^2} + {y^2} \ge 2xy \Leftrightarrow xy \le 1\) vì \({\left( {x - y} \right)^2} = {x^2} + {y^2} - 2xy \ge 0\).
+) \({x^2} - xy + {y^2} = 1 \Leftrightarrow {\left( {x + y} \right)^2} - 3xy = 1 \Leftrightarrow {\left( {x + y} \right)^2} = 1 + 3xy \ge 0 \Leftrightarrow xy \ge - \dfrac{1}{3}\).
Khi đó \(P = \dfrac{{{x^4} + {y^4} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {{x^2} + {y^2}} \right)}^2} - 2{x^2}{y^2} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {1 + xy} \right)}^2} - 2{{\left( {xy} \right)}^2} + 1}}{{xy + 2}}\).
Đặt \(t = xy,\,t \in \left[ { - \dfrac{1}{3};\,\,1} \right]\), xét hàm số \(P = \dfrac{{ - {t^2} + 2t + 2}}{{t + 2}}\)
\(P' = \dfrac{{ - {t^2} - 4t + 2}}{{{{\left( {t + 2} \right)}^2}}}\); \(P' = 0 \Leftrightarrow t = - 2 + \sqrt 6 \)
Mà \(P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(P\left( 1 \right) = 1\); \(P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Khi đó: \(m = P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(M = P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Vậy \(A = M + 15m = 17 - 2\sqrt 6 \).
Tìm tất cả những giá trị thực của \(m\) để bất phương trình sau có nghiệm với mọi \(x\) thuộc tập xác định. \(\sqrt[4]{{2x}} + \sqrt {2x} + 2\sqrt[4]{{6 - x}} + 2\sqrt {6 - x} > m\).
Xét hàm số \(f\left( x \right) = \sqrt[4]{{2x}} + \sqrt {2x} + 2\sqrt[4]{{6 - x}} + 2\sqrt {6 - x} \) trên đoạn \(\left[ {0;\,\,6} \right]\)
Ta có \(f'\left( x \right) = \dfrac{1}{2}\left( {\dfrac{1}{{\sqrt[4]{{{{\left( {2x} \right)}^3}}}}} - \dfrac{1}{{\sqrt[4]{{{{\left( {6 - x} \right)}^3}}}}}} \right) + \left( {\dfrac{1}{{\sqrt {2x} }} - \dfrac{1}{{\sqrt {6 - x} }}} \right)\)
\( \Leftrightarrow f'\left( x \right) = \left( {\dfrac{1}{{\sqrt[4]{{2x}}}} - \dfrac{1}{{\sqrt[4]{{6 - x}}}}} \right)\left[ {\dfrac{1}{2}\left( {\dfrac{1}{{\sqrt[4]{{{{\left( {2x} \right)}^2}}}}} + \dfrac{1}{{\sqrt[4]{{{{\left( {6 - x} \right)}^2}}}}} + \dfrac{1}{{\sqrt[4]{{2x\left( {6 - x} \right)}}}}} \right) + \left( {\dfrac{1}{{\sqrt[4]{{2x}}}} + \dfrac{1}{{\sqrt[4]{{6 - x}}}}} \right)} \right]\)
Vì \(\dfrac{1}{2}\left( {\dfrac{1}{{\sqrt[4]{{{{\left( {2x} \right)}^2}}}}} + \dfrac{1}{{\sqrt[4]{{{{\left( {6 - x} \right)}^2}}}}} + \dfrac{1}{{\sqrt[4]{{2x\left( {6 - x} \right)}}}}} \right) + \left( {\dfrac{1}{{\sqrt[4]{{2x}}}} + \dfrac{1}{{\sqrt[4]{{6 - x}}}}} \right) > 0,\,\,\forall x \in \left( {0;\,\,6} \right)\) nên
\(f'\left( x \right) = 0 \Leftrightarrow \dfrac{1}{{\sqrt[4]{{2x}}}} - \dfrac{1}{{\sqrt[4]{{6 - x}}}} = 0 \Leftrightarrow x = 2\)
Mà \(f\left( 0 \right) = 2\sqrt 6 + 2\sqrt[4]{6}\); \(f\left( 2 \right) = 3\sqrt 2 + 6\); \(f\left( 6 \right) = 2\sqrt 3 + \sqrt[4]{{12}}\)
Nên \(\mathop {\max }\limits_{\left[ {0;\,\,6} \right]} f\left( x \right) = f\left( 2 \right) = 3\sqrt 2 + 6\) và \(\mathop {\min }\limits_{\left[ {0;\,\,6} \right]} f\left( x \right) = f\left( 6 \right) = \sqrt[4]{{12}} + 2\sqrt 3 \)
Khi đó để bất phương trình có nghiệm với mọi \(x \in \left[ {0;\,\,6} \right]\) thì \(m < \mathop {\min }\limits_{\left[ {0;\,\,6} \right]} f\left( x \right) \Leftrightarrow m < \sqrt[4]{{12}} + 2\sqrt 3 \).
Nhà xe khoán cho hai tài xế ta-xi An và Bình mỗi người lần lượt nhận $32$ lít và $72$ lít xăng. Hỏi tổng số ngày ít nhất là bao nhiêu để hai tài xế chạy tiêu thụ hết số xăng của mình được khoán, biết rằng chỉ tiêu cho hai người một ngày tổng cộng chỉ chạy đủ hết $10$ lít xăng?
Gọi $x$ là số lít xăng mà An đã dùng trong một ngày. Với $0 < x < 10$.
$ \Rightarrow $ $10 - x$ là số lít xăng mà Bình đã dùng trong một ngày.
Khi đó
+ Để An tiêu thụ hết $32$ lít xăng cần $\dfrac{{32}}{x}$ ngày.
+ Để Bình tiêu thụ hết $72$ lít xăng cần $\dfrac{{72}}{{10 - x}}$ ngày.
Vậy tổng số ngày chạy xe của hai tài xế là
$y = \dfrac{{32}}{x} + \dfrac{{72}}{{10 - x}} \Rightarrow y' = - \dfrac{{32}}{{{x^2}}} + \dfrac{{72}}{{{{\left( {10 - x} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow x = 4$
Bảng biến thiên:
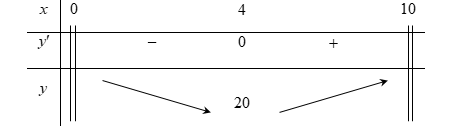
Nhìn bảng biến thiên ta thấy tổng số ngày chạy xe ít nhất của hai tài xế là \(20\) ngày.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
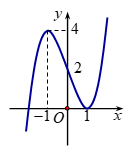
Phương trình \(\left| {f\left( {x - 2} \right) - 2} \right| = \pi \) có bao nhiêu nghiệm thực phân biệt?
Cách 1:
+ Tịnh tiến đồ thị \(y = f\left( x \right)\) sang phải $2$ đơn vị ta được đồ thị hàm số \(y = f\left( {x - 2} \right)\) (hình a)
+ Tịnh tiến đồ thị \(y = f\left( {x - 2} \right)\) xuống dưới $2$ đơn vị ta được đồ thị hàm số \(y = f\left( {x - 2} \right) - 2\) (hình b)
+ Vẽ đồ thị hàm số \(y = \left| {f\left( {x - 2} \right) - 2} \right|\) như hình c.
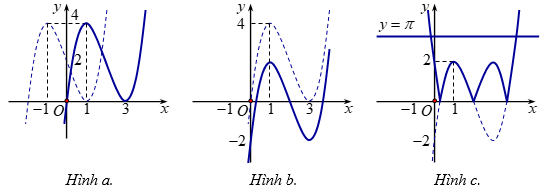
Dựa vào đồ thị hàm số \(y = \left| {f\left( {x - 2} \right) - 2} \right|\) suy ra phương trình \(\left| {f\left( {x - 2} \right) - 2} \right| = \pi \) có hai nghiệm thực phân biệt.
