Đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn được gọi là:
Đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn được gọi là trục đường tròn.
Cho hình chóp tam giác đều \(S.ABC\). Chọn kết luận không đúng:
Hình chóp \(S.ABC\) là hình chóp tam giác đều nên \(SO\) với \(O\) là tâm đáy chính là trục đường tròn đáy nên A, C đúng, D sai.
Ngoài ra \(SA = SB = SC\) nên B đúng.
Cho hai điểm \(M,N\) cố định và đường thẳng \(\Delta \) cố định thỏa mãn \(MN \bot \Delta ,d\left( {M,\Delta } \right) = d\left( {N,\Delta } \right)\). Có bao nhiêu đường tròn đi qua \(M,N\) và nhận \(\Delta \) làm trục?
Gọi \(\left( P \right)\) là mặt phẳng chứa \(MN\) và vuông góc \(\Delta \), \(O = \left( P \right) \cap \Delta \). Khi đó \(MO = NO\) nên \(M,N\) nằm trên đường tròn tâm \(O\) bán kính \(OM\).
Do \(M,N,\Delta \) cố định nên \(\left( P \right),O\) cố định và \(\left( {O,OM} \right)\) cố định và duy nhất.
Cho các hình sau đây: điểm, đường thẳng, đường tròn. Số hình khi quay quanh một trục cố định ta được mặt tròn xoay là:
Khi quay đường thẳng, đường tròn quanh một trục cố định thì ta được mặt tròn xoay.
Khi quay một điểm quanh trục cố định ta chỉ được một đường tròn.
Cho nửa đường tròn tâm \(O\) đường kính \(AB\). Khi quay nửa đường tròn quanh \(AB\) ta được:
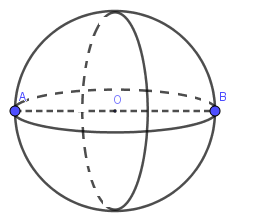
Khi quay nửa đường tròn đường kính \(AB\) quanh trục \(AB\) ta được mặt cầu đường kính \(AB\).
Quay tam giác \(ABC\) vuông tại \(A\) quanh trục \(AB\) ta được:
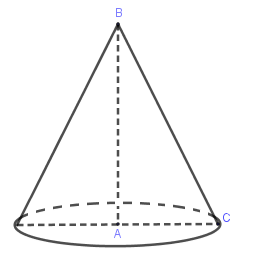
Quay hình tam giác vuông \(ABC\) quanh trục \(AB\) ta được hình nón đỉnh \(B\).
Quay hình tam giác vuông \(ABC\) tại \(A\) có \(\widehat B = {30^0}\) quanh trục là đường thẳng \(AC\) ta được hình nón có góc ở đỉnh bằng:
Quay hình tam giác vuông \(ABC\) tại \(A\) có \(\widehat B = {30^0}\) quanh trục là đường thẳng \(AC\) ta được hình nón đỉnh \(C\) có góc ở đỉnh \(2\widehat C = {120^0}\).
Chọn phát biểu đúng:
Khi quay tam giác \(ABC\) vuông tại \(A\) quanh trục \(AB\) thì
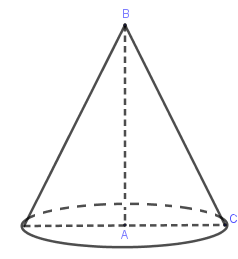
Quan sát hình vẽ ta thấy \(AB\) là đường cao.
Quay hình vuông \(ABCD\) quanh trục \(AC\) ta được:
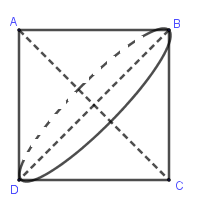
Quan sát hình vẽ ta thấy khi quay hình vuông \(ABCD\) quanh trục \(AC\) ta được \(2\) hình nón.
Số hình nón có được khi quay hình sau quanh trục \(BC\) là:
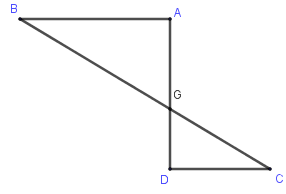
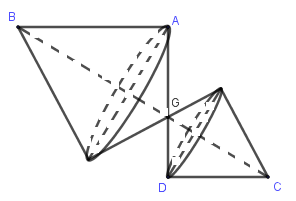
Quan sát hình vé ta thấy, có \(4\) hình nón được tạo thành.
Cho đường thẳng \(\Delta \) cố định và đường thẳng \(d//\Delta \). Quay \(d\) quanh \(\Delta \) ta được:
Quay đường thẳng \(d\) quanh \(\Delta \) ta được mặt trụ.
Quay hình chữ nhật \(ABCD\) quanh mỗi cạnh \(AB,CD\) thì ta được hai hình trụ có
Quay hình chữ nhật quanh hai cạnh đối diện ta được các hình trụ có chiều cao và bán kính đáy bằng nhau nên A đúng, B, C, D sai.
Cho hình chữ nhật \(ABCD\), khi quay hình chữ nhật quanh cạnh \(AB\) thì \(CD\) được gọi là:
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) thì được hình trụ có chiều cao \(AB\), đường sinh \(CD\) và bán kính đáy \(AD,BC\).
Do đó \(CD\) được gọi là đường sinh.
Cho hình chữ nhật \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm các cạnh \(AB,CD\). Quay hình chữ nhật quanh trục \(MN\) ta được hình trụ có bán kính đáy là:
Khi quay hình chữ nhật \(ABCD\) quanh \(MN\) ta được hình trụ có chiều cao \(MN\) và đường kính đáy \(AB,CD\) hay bán kính đáy \(AM,MB,NC,ND\).
Nếu cắt mặt trụ bởi mặt phẳng tròn xoay bởi một mặt phẳng tạo với trục một góc \(\alpha = {90^0}\) thì ta được:
Cắt mặt trụ bởi mặ phẳng tạo với trục một góc \(\alpha = {90^0}\) tức là mặt phẳng vuông góc với trục thì ta được đường tròn.
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \({45^0}\) thì ta được:
Khi cắt mặt trụ bởi mặt phẳng tạo với trục một góc \({45^0} < {90^0}\) thì ta được elip.
Nếu cắt hình trụ bởi mặt phẳng đi qua trục thì ta được thiết diện là:
Nếu cắt hình trụ bởi mặt phẳng đi qua trục thì ta được thiết diện là hình chữ nhật.
Cho hình \(\left( H \right)\) bao gồm tam giác \(ABC\) đều nội tiếp đường tròn \(\left( C \right)\). Quay hình \(\left( H \right)\) quanh trục đối xứng của nó ta được:
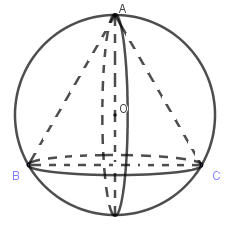
Quan sát hình vẽ ta thấy, khi quay hình \(\left( H \right)\) quanh trục đối xứng ta được hình nón nội tiếp hình cầu.
Cho hình \(\left( H \right)\) dưới đây:
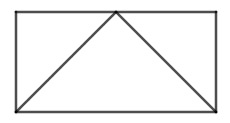
Quay hình \(\left( H \right)\) quanh trục đối xứng của nó ta được:
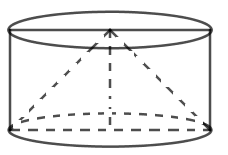
Quay hình \(\left( H \right)\) quanh trục đối xứng ta được một hình nón nội tiếp hình trụ hay hình trụ ngoại tiếp hình nón.
Trục đường tròn là đường thẳng đi qua tâm và:
- Trục của đường tròn: là đường thẳng vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.

