Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm \(y = f'\left( x \right)\) như hình vẽ
Đặt \(g\left( x \right) = 3f\left( x \right) - {x^3} + 3x - m\), với \(m\) là tham số thực. Điều kiện cần và đủ để bất phương trình \(g\left( x \right) \ge 0\) đúng với \(\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]\) là:
\(g\left( x \right) \ge 0 \Leftrightarrow 3f\left( x \right) - {x^3} + 3x - m \ge 0 \Leftrightarrow 3f\left( x \right) - {x^3} + 3x \ge m\)
Đặt \(h\left( x \right) = 3f\left( x \right) - {x^3} + 3x\). Ta có \(h'\left( x \right) = 3f'\left( x \right) - 3{x^2} + 3\)
Suy ra
\(\,\,\left\{ \begin{array}{l}h'\left( { - \sqrt 3 } \right) = 3f'\left( { - \sqrt 3 } \right) - 6 = 0\\h'\left( {\sqrt 3 } \right) = 3f'\left( {\sqrt 3 } \right) - 6 = 0\\h'\left( 0 \right) = 3f'\left( 0 \right)+3 = 0\\h'\left( \pm 1 \right) = 3f'\left( \pm 1 \right) < 0\end{array} \right.\)
Từ đó ta có bảng biến thiên:
Vậy \(h\left( x \right) \ge m \Leftrightarrow m \le h\left( {\sqrt 3 } \right) = 3f\left( {\sqrt 3 } \right)\)
Với mỗi số thực \(x\), gọi \(f\left( x \right)\) là giá trị nhỏ nhất trong các số \({g_1}\left( x \right) = 4x + 1\), \({g_2}\left( x \right) = x + 2\), \({g_3}\left( x \right) = - 2x + 4\). Giá trị lớn nhất của \(f\left( x \right)\) trên \(\mathbb{R}\) là
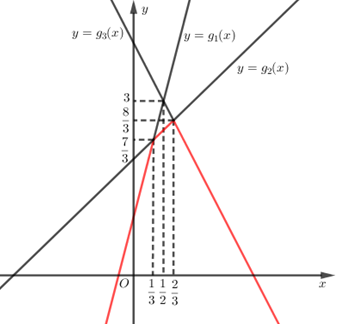
Quan sát các đồ thị hàm số ta thấy:
+ Trong nửa khoảng \(\left( { - \infty ;\dfrac{1}{3}} \right]\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_1}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là nửa đường thẳng \(y = {g_1}\left( x \right)\)
+ Trong đoạn \(\left[ {\dfrac{1}{3};\dfrac{2}{3}} \right]\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_2}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là một đoạn của đường thẳng \(y = {g_2}\left( x \right)\)
+ Trong nửa khoảng \(\left[ {\dfrac{2}{3}; + \infty } \right)\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_3}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là nửa đường thẳng \(y = {g_3}\left( x \right)\)
\( \Rightarrow \) Đồ thị hàm số \(y = f\left( x \right)\) là phần đường thẳng được tô màu đỏ.
Suy ra giá trị lớn nhất của \(f\left( x \right)\) là \(\dfrac{8}{3}\)
Biết rằng đồ thị của hàm số \(y = P\left( x \right) = {x^3} - 2{x^2} - 5x + 2\) cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là \({x_1}\), \({x_2}\), \({x_3}\). Khi đó giá trị của biểu thức \(T = \dfrac{1}{{x_1^2 - 4{x_1} + 3}} + \dfrac{1}{{x_2^2 - 4{x_2} + 3}} + \dfrac{1}{{x_3^2 - 4{x_3} + 3}}\) bằng
Xét biểu thức chia \(P\left( x \right)\) cho \({x^2} - 4x + 3\) ta được \(P\left( x \right) = \left( {x + 2} \right)\left( {{x^2} - 4x + 3} \right) - 4\)
Mà $P\left( {{x_1}} \right) = 0 \Leftrightarrow \left( {{x_1} + 2} \right)\left( {x_1^2 - 4{x_1} + 3} \right) - 4 = 0 \Leftrightarrow \dfrac{1}{{x_1^2 - 4{x_1} + 3}} = \dfrac{{{x_1} + 2}}{4}$
Tương tự, ta có $\dfrac{1}{{x_2^2 - 4{x_2} + 3}} = \dfrac{{{x_2} + 2}}{4}$; $\dfrac{1}{{x_3^2 - 4{x_3} + 3}} = \dfrac{{{x_3} + 2}}{4}$
Vậy \(T = \dfrac{{{x_1} + 2}}{4} + \dfrac{{{x_2} + 2}}{4} + \dfrac{{{x_3} + 2}}{4} = \dfrac{{{x_1} + {x_2} + {x_3} + 6}}{4} = 2\)
Mặt khác thì $\dfrac{{P'\left( x \right)}}{{P\left( x \right)}} = \dfrac{{3{x^2} - 4x - 5}}{{{x^3} - 2{x^2} - 5x + 2}} \Rightarrow \dfrac{{P'\left( 1 \right)}}{{P\left( 1 \right)}} = \dfrac{3}{2};\dfrac{{P'\left( 3 \right)}}{{P\left( 3 \right)}} = - \dfrac{5}{2} \Leftrightarrow \dfrac{1}{2}\left[ {\dfrac{{P'\left( 1 \right)}}{{P\left( 1 \right)}} - \dfrac{{P'\left( 3 \right)}}{{P\left( 3 \right)}}} \right] = 2$
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau.
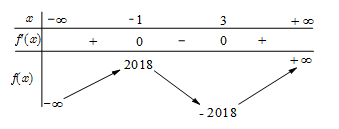
Đồ thị hàm số \(y = \left| {f\left( {x - 2017} \right) + 2018} \right|\) có bao nhiêu điểm cực trị?
Do hàm số \(g\left( x \right) = f\left( {x - 2017} \right) + 2018\) thu được bằng cách tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải một đoạn có độ dài bằng $2017$ đơn vị và tịnh tiến lên trên một đoạn có độ dài bằng $2018$ đơn vị nên ta có bảng biến thiên của hàm số \(y = g\left( x \right)\) như sau:
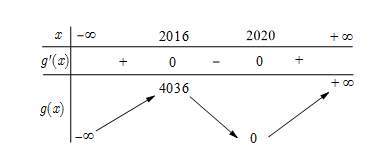
Do đó ta có bảng biến thiên của hàm số \(y = \left| {g\left( x \right)} \right|\) là:
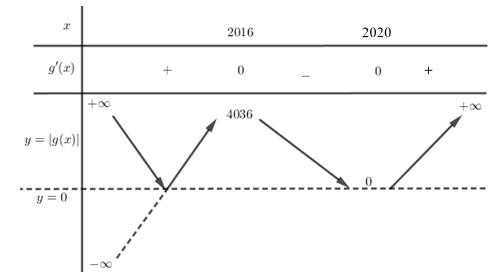
Vậy đồ thị hàm số \(y = \left| {f\left( {x - 2017} \right) + 2018} \right|\) có $3$ cực trị.
Cô An đang ở khách sạn \(A\) bên bờ biển, cô cần đi du lịch đến hòn đảo \(C\). Biết rằng khoảng cách từ đảo \(C\) đến bờ biển là \(10\;{\rm{km}}\), khoảng cách từ khách sạn \(A\) đến điểm \(B\) trên bờ gần đảo \(C\) nhất là \(50\;{\rm{km}}\). Từ khách sạn \(A\), cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo \(C\) (như hình vẽ bên). Biết rằng chi phí đi đường thủy là \(5\) USD/km, chi phí đi đường bộ là \(3\)USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
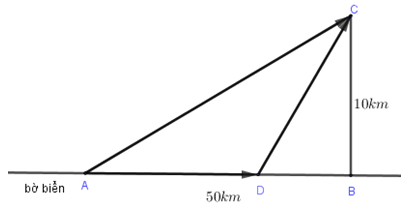
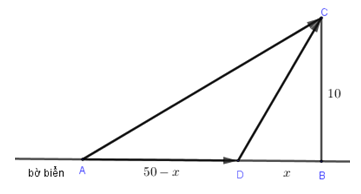
Gọi \(AD\) là quãng đường cô An đi đường bộ.
Đặt \(DB = x\,\left( {{\rm{km}}} \right)\left( {0 \le x \le 50} \right)\) \( \Rightarrow AD = 50 - x\,\left( {{\rm{km}}} \right)\).
Chi phí của cô An: \(f\left( x \right) = \left( {50 - x} \right)3 + \sqrt {{x^2} + {{10}^2}} {\rm{.5 }}\left( {{\rm{USD}}} \right)\)
\(f\left( x \right)\) liên tục trên \(\left[ {0;50} \right]\).
Ta có $f'\left( x \right) = - 3 + 5.\dfrac{{x{\rm{ }}}}{{\sqrt {{x^2} + 100} }}$$ = \dfrac{{ - 3\sqrt {{x^2} + 100} + 5x{\rm{ }}}}{{\sqrt {{x^2} + 100} }}$
$f'\left( x \right) = 0$$ \Leftrightarrow - 3\sqrt {{x^2} + 100} + 5x{\rm{ }} = 0$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\9\left( {{x^2} + 100} \right) = 25{x^2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = \dfrac{{9.100}}{{16}}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x = \dfrac{{15}}{2}\end{array} \right.$.
Ta có \(f\left( 0 \right) = 200;\,\,f\left( {50} \right) = 50\sqrt {26} ;\,\,f\left( {\dfrac{{15}}{2}} \right) = 190\)
Để chi phí ít nhất thì $x = \dfrac{{15}}{2}$.
Vậy cô An phải đi đường bộ một khoảng: \(AD = 50 - \dfrac{{15}}{2} = \dfrac{{85}}{2}\left( {{\rm{km}}} \right)\) để chi phí ít nhất.
Tìm tập hợp $S$ tất cả các giá trị của tham số thực $m$ để đồ thị hàm số $y = {x^4} - 2{m^2}{x^2} + {m^4} + 3$ có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ $O$ tạo thành một tứ giác nội tiếp.
\(y' = 4{x^3} - 4{m^2}x\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm m.\end{array} \right.\)
Để hàm số có 3 cực trị thì phương trình \(y' = 0\) có 3 nghiệm, hay \(m \ne 0\).
Không mất tính tổng quát giả sử 3 điểm cực trị có tọa độ \(A\left( {0;\,\,{m^4} + 3} \right)\); \(B\left( {m;3} \right)\);\(C\left( { - m;3} \right)\).
Ta có \(\overrightarrow {AC} \left( { - m; - {m^4}} \right);\,\,\overrightarrow {OC} \left( { - m;3} \right)\)
Tứ giác \(OBAC\) có \(\left\{ \begin{array}{l}AB = AC\\OB = OC\end{array} \right.\).
Suy ra \(OA\) là đường trung trực của \(BC\).
Để tứ giác \(OBAC\) nội tiếp đường tròn thì điểm \(B\), \(C\) phải nhìn cạnh \(OA\) dưới góc \(90^\circ .\)
Khi đó \(\overrightarrow {AC} .\overrightarrow {OC} = 0 \Leftrightarrow {m^2} - 3{m^4} = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0:L\\m = \pm \sqrt {\dfrac{1}{3}} :T/m\end{array} \right.\).
Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được \(220500\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) nước. Biết tỉ lệ giữa chiều cao và chiều rộng của bể bằng \(3\). Xác định diện tích đáy của bể cá để tiết kiệm nguyên vật liệu nhất.
Gọi \(a\), \(b\), \(c > 0\) lần lượt là chiều rộng, dài, cao của hình hộp chữ nhật.
Theo đề \(V = abc = 220500\) và \(c = 3a \Rightarrow 3{a^2}b = 220500 \Rightarrow ab = \dfrac{{73500}}{a}\)
Ta có \({S_{tp}} = ab + 2ac + 2bc\)\( = ab + 6{a^2} + 6ab = 7ab + 6{a^2}\)
\( = \dfrac{{514500}}{a} + 6{a^2}\)\( = 6\left( {\dfrac{{42875}}{a} + \dfrac{{42875}}{a} + {a^2}} \right)\)
\({S_{tp}} = 6\left( {\dfrac{{42875}}{a} + \dfrac{{42875}}{a} + {a^2}} \right) \ge 6.3\sqrt[3]{{\dfrac{{42875}}{a}.\dfrac{{42875}}{a}.{a^2}}} = 22050.\)
Suy ra \({S_{tp}}\) nhỏ nhất khi $\dfrac{42875}{a}={{a}^{2}}\Leftrightarrow a=35\Rightarrow b=60\Rightarrow {{S}_{}}=2100\,\,\,\text{c}{{\text{m}}^{\text{2}}}$
Cho hàm số \(y = {x^4} - 2m{x^2} + m\), có đồ thị \(\left( C \right)\) với \(m\) là tham số thực. Gọi \(A\) là điểm thuộc đồ thị \(\left( C \right)\) có hoành độ bằng \(1\). Tìm \(m\) để tiếp tuyến \(\Delta \) với đồ thị \(\left( C \right)\) tại \(A\) cắt đường tròn \(\left( \gamma \right):\,{x^2} + {\left( {y - 1} \right)^2} = 4\) tạo thành một dây cung có độ dài nhỏ nhất
Đường tròn \(\left( \gamma \right):\,{x^2} + {\left( {y - 1} \right)^2} = 4\) có tâm \(I\left( {0;\,1} \right)\), \(R = 2\)
Ta có \(A\left( {1;\,1 - m} \right)\); \(y' = 4{x^3} - 4mx \Rightarrow y'\left( 1 \right) = 4 - 4m\)
Suy ra phương trình \(\Delta \): \(y = \left( {4 - 4m} \right)\left( {x - 1} \right) + 1 - m\).
Dễ thấy \(\Delta \) luôn đi qua điểm cố định $F\left( {\dfrac{3}{4};\,0} \right)$ và điểm $F$ nằm trong đường tròn \(\left( \gamma \right)\)
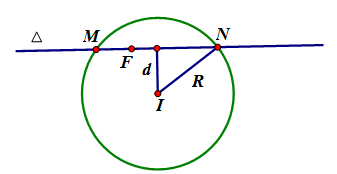
Giả sử \(\Delta \) cắt \(\left( \gamma \right)\) tại \(M\), \(N\). Thế thì ta có: \(MN = 2\sqrt {{R^2} - {d^2}\left( {I;\,\Delta } \right)} = 2\sqrt {4 - {d^2}\left( {I;\,\Delta } \right)} \)
Do đó \(MN\) nhỏ nhất $ \Leftrightarrow d\left( {I;\,\Delta } \right)$ lớn nhất $ \Leftrightarrow d\left( {I;\,\Delta } \right) = IF$$ \Rightarrow \Delta \bot IF$
Khi đó đường \(\Delta \) có 1 vectơ chỉ phương $\vec u \bot \overrightarrow {IF} = \left( {\dfrac{3}{4};\, - 1} \right)$; \(\vec u = \left( {1;\,\,4 - 4m} \right)\) nên ta có:
$\overrightarrow u .\overrightarrow {IF} = 0 \Leftrightarrow 1.\dfrac{3}{4} - \left( {4 - 4m} \right) = 0$$ \Leftrightarrow m = \dfrac{{13}}{{16}}$
Cho hàm số $f\left( x \right)$ có đồ thị là đường cong $\left( C \right)$, biết đồ thị của $f'\left( x \right)$ như hình vẽ:
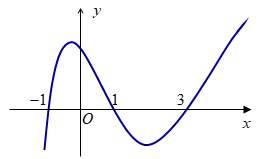
Tiếp tuyến của $\left( C \right)$ tại điểm có hoành độ bằng $1$ cắt đồ thị $\left( C \right)$ tại hai điểm $A$, $B$ phân biệt lần lượt có hoành độ $a$, $b$. Chọn khẳng định đúng trong các khẳng định sau:
Từ đồ thị, ta có $f'\left( 1 \right) = 0$.
Phương trình tiếp tuyến của $\left( C \right)$ tại điểm có hoành độ bằng $1$ có dạng: $y = f'\left( 1 \right)\left( {x - 1} \right) + f\left( 1 \right) \Leftrightarrow y = f\left( 1 \right)$.
Phương trình hoành độ giao điểm của tiếp tuyến trên với đồ thị $\left( C \right)$: $f\left( x \right) = f\left( 1 \right)$.
Từ đồ thị, ta có $f'\left( { - 1} \right) = f'\left( 3 \right) = 0$. Ta được bảng biến thiên của hàm số $y = f\left( x \right)$.
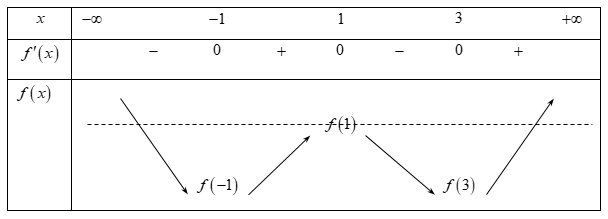
Từ bảng biến thiên, ta thấy đường thẳng $y = f\left( 1 \right)$ cắt đồ thị hàm số tại ba điểm có hoành độ lần lượt là $1$, $a$, $b$ với $a < - 1$ và $b > 3$. Như vậy đáp án D đúng, các khẳng định A, B, C đều không thỏa điều trên.
Cho hàm số \(y = {\left( {x - m} \right)^3} - 3x + {m^2}\) có đồ thị là \(\left( {{C_m}} \right)\) với \(m\) là tham số thực. Biết điểm \(M\left( {a;\,\,b} \right)\) là điểm cực đại của \(\left( {{C_m}} \right)\) ứng với một giá trị \(m\) thích hợp, đồng thời là điểm cực tiểu của \(\left( {{C_m}} \right)\) ứng với một giá trị khác của \(m\). Tổng \(S = 2018a + 2020b\) bằng
Vì điểm \(M\left( {a;\,\,b} \right)\) thuộc đồ thị \(\left( {{C_m}} \right)\) nên ta có: \({\left( {a - m} \right)^3} - 3a + {m^2} = b,\forall m \in \mathbb{R}\). \(\left( 1 \right)\)
Xét \(y' = 3{\left( {x - m} \right)^2} - 3\); \(y' = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = m - 1\\x = m + 1\end{array} \right.\).
Bảng biến thiên
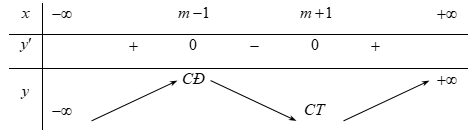
Dựa vào bảng biến thiên, ta có:
Nếu \({m_1}\) là giá trị của tham số \(m\) để đồ thị hàm số nhận điểm $M\left( {a;\,\,b} \right)$ là điểm cực đại thì \(a = {m_1} - 1\). Nếu \({m_2}\) là giá trị của tham số \(m\) để đồ thị hàm số nhận điểm $M\left( {a;\,\,b} \right)$ là điểm cực tiểu thì \(a = {m_2} + 1\)
Do đó $m_1=a+1,m_2=a-1$
Mà \({m_1}\), \({m_2}\) phải thỏa mãn \(\left( 1 \right)\) nên ta có: \(\left\{ \begin{array}{l} - 1 - 3a + {\left( {a + 1} \right)^2} = b\\1 - 3a + {\left( {a - 1} \right)^2} = b\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = - \dfrac{1}{4}\end{array} \right.\)
Vậy \(S = 2018a + 2020b = 504\)
