Câu hỏi:
2 năm trước
Cho hàm số y=f(x) có bảng biến thiên như sau.
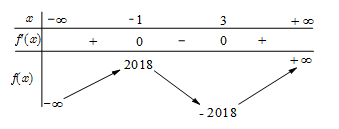
Đồ thị hàm số y=|f(x−2017)+2018| có bao nhiêu điểm cực trị?
Trả lời bởi giáo viên
Đáp án đúng: b
Do hàm số g(x)=f(x−2017)+2018 thu được bằng cách tịnh tiến đồ thị hàm số y=f(x) sang phải một đoạn có độ dài bằng 2017 đơn vị và tịnh tiến lên trên một đoạn có độ dài bằng 2018 đơn vị nên ta có bảng biến thiên của hàm số y=g(x) như sau:
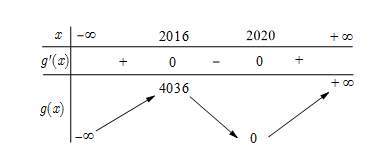
Do đó ta có bảng biến thiên của hàm số y=|g(x)| là:
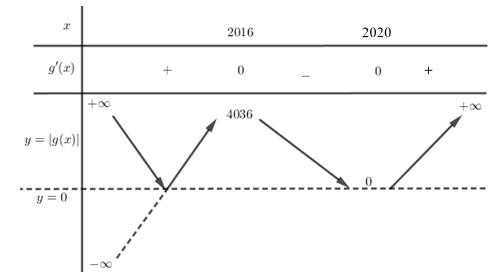
Vậy đồ thị hàm số y=|f(x−2017)+2018| có 3 cực trị.
Hướng dẫn giải:
- Lập bảng biến thiên của hàm số y=f(x−2017)+2018
- Từ đó suy ra bảng biến thiên của hàm số y=|f(x−2017)+2018| và kết luận đáp án đúng.