Với mỗi số thực \(x\), gọi \(f\left( x \right)\) là giá trị nhỏ nhất trong các số \({g_1}\left( x \right) = 4x + 1\), \({g_2}\left( x \right) = x + 2\), \({g_3}\left( x \right) = - 2x + 4\). Giá trị lớn nhất của \(f\left( x \right)\) trên \(\mathbb{R}\) là
Trả lời bởi giáo viên
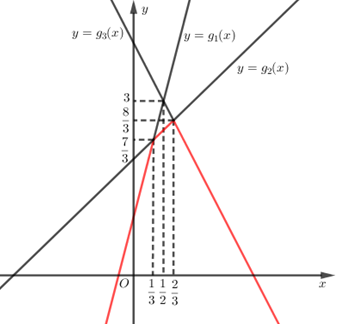
Quan sát các đồ thị hàm số ta thấy:
+ Trong nửa khoảng \(\left( { - \infty ;\dfrac{1}{3}} \right]\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_1}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là nửa đường thẳng \(y = {g_1}\left( x \right)\)
+ Trong đoạn \(\left[ {\dfrac{1}{3};\dfrac{2}{3}} \right]\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_2}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là một đoạn của đường thẳng \(y = {g_2}\left( x \right)\)
+ Trong nửa khoảng \(\left[ {\dfrac{2}{3}; + \infty } \right)\) thì \(\min \left\{ {{g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)} \right\} = {g_3}\left( x \right)\) nên đồ thị hàm số \(y = f\left( x \right)\) là nửa đường thẳng \(y = {g_3}\left( x \right)\)
\( \Rightarrow \) Đồ thị hàm số \(y = f\left( x \right)\) là phần đường thẳng được tô màu đỏ.
Suy ra giá trị lớn nhất của \(f\left( x \right)\) là \(\dfrac{8}{3}\)
Hướng dẫn giải:
- Vẽ các đồ thị hàm số \(y = {g_1}\left( x \right);\) \(y = {g_2}\left( x \right);\) \(y = {g_3}\left( x \right)\) trên cùng một hệ trục tọa độ.
- Tìm đồ thị hàm số \(y = f\left( x \right)\) trên từng khoảng và suy ra đồ thị hàm số \(y = f\left( x \right)\) trên \(R\)
- Tìm \(GTLN\) của \(f\left( x \right)\) và kết luận.