Cho hàm số \(y = {x^3} - 3x + 1\). Mệnh đề nào sau đây đúng?
TXĐ: \(D = \mathbb{R}\). Ta có \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\).
Bảng xét dấu \(y'\) :

\( \Rightarrow \) Hàm số đã cho đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\) và nghịch biến trên \(\left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Nhìn trên đồ thị ta thấy khi \(x\) tăng trong \(\left( {0;2} \right)\) thì đồ thị hàm số \(f\left( x \right)\) đi lên \( \Rightarrow \) giá trị tung độ tăng \( \Rightarrow \) Hàm số đồng biến trên \(\left( {0;2} \right)\).
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số đã cho đồng biến trên khoảng \(( - 2;0)\)
Cho phương trình \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt?
ĐKXĐ: \(x \ge \dfrac{m}{4}\)
Ta có: \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\\ \Leftrightarrow {x^3} + 12x = \left( {4x - m} \right)\sqrt {4x - m} + 12\sqrt {4x - m} \)
\( \Leftrightarrow {x^3} + 12x = {\left( {\sqrt {4x - m} } \right)^3} + 12\sqrt {4x - m} (*)\)
Xét hàm số \(f\left( t \right) = {t^3} + 12t,\,\,\,f'\left( t \right) = 3{t^2} + 12 > 0,\,\forall t \Rightarrow \) Hàm số đồng biến trên \(\mathbb{R}\)
Phương trình (*) trở thành
\( f\left( x \right) = f\left( {\sqrt {4x - m} } \right)\)
\( \Leftrightarrow x = \sqrt {4x - m} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 4x - m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\m = 4x - {x^2} = g\left( x \right)\end{array} \right.\)

Phương trình đã cho có hai nghiệm thực phân biệt \( \Leftrightarrow 0 \le m < 4 \Rightarrow m \in \left\{ {0;1;2;3} \right\}\): 4 giá trị thỏa mãn.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?
Dựa vào BBT ta thấy hàm số đã cho nghịch biến trên khoảng \(\left( {0\,;\,\,1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Quan sát đồ thị hàm số ta thấy trong khoảng \(\left( { - 1;0} \right)\) thì đồ thị hàm số đi lên nên hàm số đồng biến trong khoảng \(\left( { - 1;0} \right)\).
Hàm số \(y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1\) nghịch biến trên khoảng \(\left( {1;3} \right)\) khi và chỉ khi:
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 6{x^2} - 6\left( {m + 1} \right)x + 6m\).
Xét \(y' = 0 \Leftrightarrow {x^2} - \left( {m + 1} \right)x + m = 0\).
Ta có \(\Delta = {\left( {m + 1} \right)^2} - 4m = {\left( {m - 1} \right)^2} \ge 0\)\(\forall m\)
+) Với \(m = 1\) ta có \(y' = 6{x^2} - 12x + 6 = 6{\left( {x - 1} \right)^2} \ge 0\)\(\forall x \in \left( {1;3} \right)\), do đó hàm số đồng biến trên \(\left( {1;3} \right)\) (loại).
+) Với \(m \ne 1 \Rightarrow \Delta > 0\,\,\forall m\), suy ra phương trình \(y' = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{m + 1 + m - 1}}{2} = m\\{x_2} = \dfrac{{m + 1 - m + 1}}{2} = 1\end{array} \right.\).
Ta có bảng xét dấu:
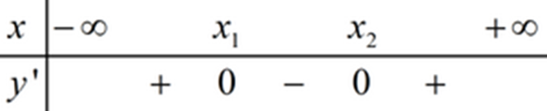
Từ BXD ta thấy để hàm số nghịch biến trên \(\left( {1;3} \right)\) thì \(y' \le 0\,\,\forall x \in \left( {1;3} \right)\) \( \Rightarrow \left( {1;3} \right) \subset \left( {{x_1};{x_2}} \right)\)
\( \Rightarrow \left[ \begin{array}{l}\left( {1;3} \right) \subset \left( {1;m} \right)\\\left( {1;3} \right) \subset \left( {m;1} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 \le 1 < 3 \le m\\m \le 1 < 3 \le 1\,\,\left( \text{Loại} \right)\end{array} \right. \)
$\Leftrightarrow m \ge 3\,\,\left( {tm} \right)$
Vậy \(m \ge 3\).
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\) ?
\(y = - {x^3} - x\) \( \Rightarrow {y^\prime } = - {x^2} - 1 = - \left( {{x^2} + 1} \right) < 0\forall x \in \mathbb{R}\)
Hàm số \(y = - {x^3} - x\) nghịch biến trên \(\mathbb{R}\)
Tập tất cả giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3m{x^2} + 3x + 1\) đồng biến trên \(\mathbb{R}\) là
Hàm số đã cho là hàm số bậc ba có \(a = 1 > 0\), có: \(y' = 3{x^2} - 6mx + 3\).
Do đó nó đồng biến trên \(\mathbb{R}\) nếu và chỉ nếu phương trình \(y' = 0\) vô nghiệm hoặc có nghiệm kép \( \Leftrightarrow \Delta ' = 9{m^2} - 9 \le 0 \Leftrightarrow - 1 \le m \le 1\).
Vậy \(m \in \left[ { - 1;1} \right]\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(D\). Nếu với mọi \({x_1},{x_2} \in D\) mà \({x_1} < {x_2}\) ta đều có \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) thì:
Hàm số \(y = f\left( x \right)\) thỏa mãn nếu với mọi \({x_1},{x_2} \in D\) mà \({x_1} < {x_2}\) ta đều có \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) thì hàm số đồng biến trên \(D\)
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm trên \(R\). Chọn kết luận đúng:
Đáp án A: Nếu \(f'\left( x \right) > 0,\forall x \in R\) thì hàm số \(y = f\left( x \right)\) đồng biến trên \(R\) nên A đúng.
Đáp án B: Nếu \(f'\left( x \right) < 0,\forall x \in R\) thì hàm số nghịch biến trên \(R\) nên B sai.
Đáp án C, D: Nếu \(f'\left( x \right) = 0,\forall x \in R\) thì hàm số không đổi trên \(R\) nên C, D sai.
Cho hàm số \(y = f\left( x \right)\) nghịch biến trên \(D\) và \({x_1},{x_2} \in D\) mà \({x_1} > {x_2}\), khi đó:
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(D\) thì với mọi \({x_1},{x_2} \in D\) mà \({x_1} > {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) đồng biến trên \(R\) thì:
Hàm số \(y = f\left( x \right)\) đồng biến trên \(R\) thì \(f'\left( x \right) \ge 0,\forall x \in R\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(D\). Nếu với mọi \({x_1},{x_2} \in D\) mà \({x_1} < {x_2}\) ta đều có \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\) thì:
Hàm số \(y = f\left( x \right)\) thỏa mãn nếu với mọi \({x_1},{x_2} \in D\) mà \({x_1} < {x_2}\) ta đều có \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\) thì hàm số nghịch biến trên \(D\)
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(R\). Nếu hàm số \(f\left( x \right)\) nghịch biến trên \(R\) thì:
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(R\) thì \(f'\left( x \right) \le 0,\forall x \in R\).
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = - {x^2} - 1\) trên \(R\), chọn kết luận đúng:
Ta có: \(f'\left( x \right) = - {x^2} - 1 < 0,\forall x \in R\) nên hàm số nghịch biến trên \(R\).
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm trên \(\left( { - 5;5} \right)\). Khi đó:
Vì \(y = f\left( x \right)\) đồng biến trên \(\left( { - 5;5} \right)\) nên \(f'\left( x \right) \ge 0,\forall x \in \left( { - 5;5} \right)\).
Do đó \(f'\left( 3 \right) \ge 0,\) \(f'\left( 0 \right) \ge 0\) nên các đáp án A, B, D đều sai.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
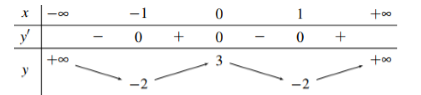
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Từ BBT ta thấy hàm số đồng biến trên \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\)
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = {x^2} + 2\) trên \(R\), chọn kết luận đúng:
Ta có: \(f'\left( x \right) = {x^2} + 2 > 0,\forall x \in R\) nên hàm số đồng biến trên \(R\).
Cho hàm số có bảng biến thiên như sau:
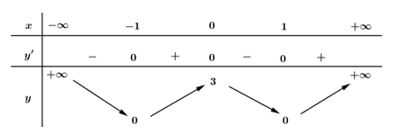
Mệnh đề nào dưới đây đúng?
Dựa vào bàng biến thiên ta thấy hàm số đồng biến trên các khoảng $\left( { - 1;\;0} \right)$ và $\left( {1; + \infty {\rm{\;}}} \right).$
Hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 1} \right)$ và $\left( {0;\;1} \right).$

