Hàm số \(y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1\) nghịch biến trên khoảng \(\left( {1;3} \right)\) khi và chỉ khi:

TXĐ: \(D = \mathbb{R}\).

Ta có \(y' = 6{x^2} - 6\left( {m + 1} \right)x + 6m\).

Xét \(y' = 0 \Leftrightarrow {x^2} - \left( {m + 1} \right)x + m = 0\).

Ta có \(\Delta  = {\left( {m + 1} \right)^2} - 4m = {\left( {m - 1} \right)^2} \ge 0\)\(\forall m\)

+) Với \(m = 1\) ta có \(y' = 6{x^2} - 12x + 6 = 6{\left( {x - 1} \right)^2} \ge 0\)\(\forall x \in \left( {1;3} \right)\), do đó hàm số đồng biến trên \(\left( {1;3} \right)\) (loại).

+) Với \(m \ne 1 \Rightarrow \Delta  > 0\,\,\forall m\), suy ra phương trình \(y' = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{m + 1 + m - 1}}{2} = m\\{x_2} = \dfrac{{m + 1 - m + 1}}{2} = 1\end{array} \right.\).

Ta có bảng xét dấu:

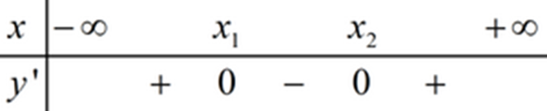
Từ BXD ta thấy để hàm số nghịch biến trên \(\left( {1;3} \right)\) thì \(y' \le 0\,\,\forall x \in \left( {1;3} \right)\) \( \Rightarrow \left( {1;3} \right) \subset \left( {{x_1};{x_2}} \right)\)

\( \Rightarrow \left[ \begin{array}{l}\left( {1;3} \right) \subset \left( {1;m} \right)\\\left( {1;3} \right) \subset \left( {m;1} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 \le 1 < 3 \le m\\m \le 1 < 3 \le 1\,\,\left( \text{Loại} \right)\end{array} \right. \)

$\Leftrightarrow m \ge 3\,\,\left( {tm} \right)$

Vậy \(m \ge 3\).