Có bao nhiêu số nguyên \(m \in \left( { - 7;7} \right)\) để đồ thị hàm số \(y = \left| {{x^4} - 3m{x^2} - 4} \right|\) có đúng ba điểm cực trị \(A,B,C\) và diện tích tam giác \(ABC\) lớn hơn 4.
Xét hàm số \(y = f\left( x \right) = {x^4} - 3m{x^2} - 4,\,\,\,\,f'\left( x \right) = 4{x^3} - 6mx,\,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = \dfrac{{3m}}{2}\end{array} \right.\)
+) TH1: \(m \le 0\):
Đồ thị hàm số \(y = f\left( x \right)\) có duy nhất 1 điểm cực trị là \(M\left( {0; - 4} \right)\) (cực tiểu)
Khi đó, đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có đúng 3 điểm cực trị là \(A\left( {0; 4} \right)\), \(B\left( {{x_1};0} \right),\,\,C\left( {{x_2};0} \right),\,\,\left( {{x_1} < {x_2}} \right)\) (B, C chính là giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và trục hoành)
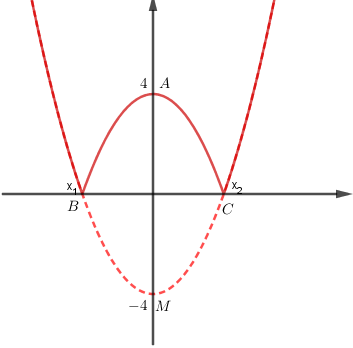
Giải phương trình: \({x^4} - 3m{x^2} - 4 = 0 \Leftrightarrow {x^2} = \dfrac{{3m + \sqrt {9{m^2} + 16} }}{2} \)
$\Leftrightarrow {x_{1,2}} = \dfrac{{ \pm \sqrt {3m + \sqrt {9{m^2} + 16} } }}{{\sqrt 2 }} $ $\Rightarrow {x_2} - {x_1} = \sqrt 2 .\sqrt {3m + \sqrt {9{m^2} + 16} } $
Diện tích tam giác \(ABC\) là:
$\dfrac{1}{2}.4.\sqrt 2 .\sqrt {3m + \sqrt {9{m^2} + 16} } > 4 $ $\Leftrightarrow \sqrt {3m + \sqrt {9{m^2} + 16} } > \sqrt 2 $
$ \Leftrightarrow 3m + \sqrt {9{m^2} + 16} > 2$ $ \Leftrightarrow \sqrt {9{m^2} + 16} > 2 - 3m$
\( \Leftrightarrow 9{m^2} + 16 > {\left( {2 - 3m} \right)^2}\) (do \(m \le 0\))
\( \Leftrightarrow 9{m^2} + 16 > 4 - 12m + 9{m^2} \) \(\Leftrightarrow m > - 1\,\, \Rightarrow - 1 < m \le 0\)
+) TH2: \(m > 0\)
Đồ thị hàm số \(y = f\left( x \right)\) có 3 điểm cực trị là \(M\left( {0; -4} \right)\) (cực tiểu), \(B\left( { - \sqrt {\dfrac{{3m}}{2}} ;{y_0}} \right),\,\,C\left( {\sqrt {\dfrac{{3m}}{2}} ;{y_0}} \right)\)
Với \({y_0} = f\left( {\sqrt {\dfrac{{3m}}{2}} } \right) = \dfrac{{9{m^2}}}{4} - 3m.\dfrac{{3m}}{2} - 4 = - \dfrac{{9{m^2}}}{4} - 4 < 0,\forall m\)
Khi đó, đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có đúng 5 điểm cực trị \( \Rightarrow \) Loại.
Vậy, \( - 1 < m \le 0\).
Mà \(m \in \left( { - 7;7} \right),\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ 0 \right\}\): 1 giá trị.
Cho hàm số \(y = {x^3} - 6mx + 4\) có đồ thị \(\left( {{C_m}} \right)\). Gọi \({m_0}\) là giá trị của \(m\) để đường thẳng đi qua điểm cực đại, điểm cực tiểu của \(\left( {{C_m}} \right)\) cắt đường tròn tâm \(I\left( {1;0} \right)\), bán kính \(\sqrt 2 \) tại hai điểm phân biệt \(A,B\) sao cho tam giác \(IAB\) có diện tích lớn nhất. Chọn khẳng định đúng?
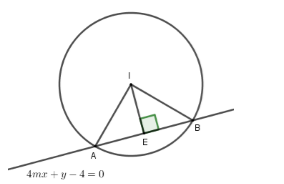
Ta có: \(y' = 3{x^2} - 6m \Rightarrow y = y'.\left( {\dfrac{1}{3}x} \right) - 4mx + 4\).
Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là \(y = - 4mx + 4 \Leftrightarrow 4mx + y - 4 = 0\).
Diện tích tam giác \(IAB\) là \({S_{IAB}} = \dfrac{1}{2}IA.IB.\sin \widehat {AIB} = \dfrac{1}{2}.\sqrt 2 .\sqrt 2 .\sin \widehat {AIB} = \sin \widehat {AIB} \le 1\)
\( \Rightarrow {S_{IAB}}\) đạt GTLN khi \(\sin \angle AIB = 1 \Leftrightarrow IA \bot IB\) hay tam giác \(IAB\) vuông cân tại \(I\) và \(IA = IB = \sqrt 2 \)\( \Rightarrow AB = 2 \Rightarrow d\left( {I,AB} \right) = \dfrac{1}{2}AB = 1.\)
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {4m.1 + 0 - 4} \right|}}{{\sqrt {{{\left( {4m} \right)}^2} + {1^2}} }} = 1 \Leftrightarrow \left| {4m - 4} \right| = \sqrt {{{\left( {4m} \right)}^2} + {1^2}} \\ \Leftrightarrow 16{m^2} - 32m + 16 = 16{m^2} + 1 \Leftrightarrow m = \dfrac{{15}}{{32}} \in \left( {0;1} \right)\end{array}\)
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - \left( {2m - 1} \right){x^2} + \left( {{m^2} - m + 7} \right)x + m - 5\) có hai điểm cực trị là độ dài hai cạnh góc vuông của một tam giác vuông có cạnh huyền bằng \(\sqrt {74} \).
Ta có: \(y' = {x^2} - 2\left( {2m - 1} \right)x + {m^2} - m + 7\).
Điều kiện bài toán tương đương tìm \(m\) để phương trình \(y' = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 74\).
+) Phương trình \(y' = 0\) có hai nghiệm dương phân biệt \({x_1},{x_2}\)
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {2m - 1} \right)^2} - \left( {{m^2} - m + 7} \right) > 0\\2\left( {2m - 1} \right) > 0\\{m^2} - m + 7 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{m^2} - 3m - 6 > 0\\2m - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m > \dfrac{1}{2}\end{array} \right. \Leftrightarrow m > 2\)
Khi đó:
\(\begin{array}{l}x_1^2 + x_2^2 = 74 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 74\\ \Rightarrow 4{\left( {2m - 1} \right)^2} - 2\left( {{m^2} - m + 7} \right) = 74\\ \Leftrightarrow 4\left( {4{m^2} - 4m + 1} \right) - 2{m^2} + 2m - 14 - 74 = 0\\ \Leftrightarrow 14{m^2} - 14m - 84 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,\,\,\left( {tm} \right)\\m = - 2\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 3\).
Tìm tất cả các giá trị thực của tham số m để hàm số $y = {x^3} - 3{x^2} + (m + 1)x + 2$ có hai điểm cực trị.
$y = {x^3} - 3{x^2} + (m + 1)x + 2 \Rightarrow y' = 3{x^2} - 6x + m + 1$
Hàm số $y = {x^3} - 3{x^2} + (m + 1)x + 2$ có hai điểm cực trị $ \Leftrightarrow y' = 0$ có 2 nghiệm phân biệt
$ \Leftrightarrow \Delta ' > 0 \Leftrightarrow {3^2} - 3.(m + 1) > 0 \Leftrightarrow m < 2$
Tìm tất cả các giá trị thực của $m$ để hàm số $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2$ có cực đại, cực tiểu
Ta có: $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2 \Rightarrow y' = 4{x^3} + 4x\left( {{m^2} - 9} \right) = 4x\left( {{x^2} + {m^2} - 9} \right)$
$y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = 9 - {m^2}\left( 1 \right)}\end{array}} \right.$
Hàm số đã cho có cực đại, cực tiểu khi và chỉ khi phương trình $\left( 1 \right)$có hai nghiệm phân biệt khác 0
$ \Leftrightarrow 9 - {m^2} > 0 \Leftrightarrow {\rm{\;}} - 3 < m < 3$
Hàm số $y = m{x^4} + \left( {m + 3} \right){x^2} + 2m - 1$ chỉ có cực đại mà không có cực tiểu khi
+) Với \(m = 0\) thì ta có hàm số \(y = 3{x^2} - 1\) có \(3 > 0\) nên đồ thị hàm số là một parabol có bề lõm hướng lên trên\( \Rightarrow \) hàm số có điểm cực tiểu \(x = 0\).
+) Với \(m \ne 0\) ta có hàm trùng phương \(y = m{x^4} + \left( {m + 3} \right){x^2} + 2m - 1\)
\( \Rightarrow y' = 4m{x^3} + 2\left( {m + 3} \right)x = x\left( {4m{x^2} + 2m + 6} \right)\), \(y'' = 12m{x^2} + 2\left( {m + 3} \right)\).
Xét phương trình \(y' = 0\) \( \Leftrightarrow x\left( {4m{x^2} + 2m + 6} \right) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = \dfrac{{ - m - 3}}{{2m}}{\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Nếu hàm số có cực đại mà không có cực tiểu thì phương trình \(y' = 0\) có nghiệm \(x = 0\) duy nhất .
Hay phương trình (2) vô nghiệm hoặc có nghiệm kép \(x = 0\)
\( \Leftrightarrow \dfrac{{ - m - 3}}{{2m}} \le 0 \Leftrightarrow \dfrac{{m + 3}}{{2m}} \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \le {\rm{\;}} - 3}\\{m > 0}\end{array}} \right.\)
Với \(m > 0\) thì phương trình \(y' = 0\) có nghiệm duy nhất \(x = 0\) và \(y''\left( 0 \right) = 2\left( {m + 3} \right) > 0\), do đó \(x = 0\) là điểm cực tiểu của hàm số (loại).
Với \(m < - 3\) thì \(y''\left( 0 \right) = 2\left( {m + 3} \right) < 0\), do đó \(x = 0\) là điểm cực đại (nhận).
Với \(m = - 3\) thì \(y' = - 12{x^3} = 0 \Leftrightarrow x = 0\) và \(y'\) đổi dấu từ dương sang âm qua nghiệm \(x = 0\).
Do đó \(x = 0\) là điểm cực đại của hàm số (nhận).
Vậy \(m \le - 3\).
Hàm số $y = {x^3} + 2a{x^2} + 4bx - 2018,{\mkern 1mu} {\mkern 1mu} (a,{\mkern 1mu} b \in R)$ đạt cực trị tại $x = - 1$ . Khi đó hiệu $a - b$ là:
$y = {x^3} + 2a{x^2} + 4bx - 2018,{\mkern 1mu} {\mkern 1mu} (a,{\mkern 1mu} b \in R) \Rightarrow y' = 3{x^2} + 4ax + 4b$
Hàm số trên đạt cực trị tại $x = - 1$
$ \Rightarrow 3{( - 1)^2} + 4a.( - 1) + 4b = 0 $ $\Leftrightarrow 3 - 4a + 4b = 0 \Leftrightarrow 3 - 4(a - b) = 0 $ $\Leftrightarrow a - b = \dfrac{3}{4}$
Tìm tất cả các giá trị thực của m để hàm số \(y = 4{x^3} + m{x^2} - 12x\) đạt cực tiểu tại điểm $x = - 2$.
Ta có \(\left\{ \begin{array}{l}y' = 12{x^2} + 2mx - 12\\y'' = 24x + 2m\end{array} \right.\) .
Từ giả thiết bài toán ta phải có \(y'\left( { - 2} \right) = 48 - 4m - 12 = 0 \Leftrightarrow m = 9.\)
Thay vào \(y''\left( { - 2} \right) = - 48 + 2m = - 48 + 18 = - 30 < 0\).
Khi đó, hàm số đạt cực đại tại $x = - 2$.
Vậy không có giá trị \(m\) thỏa mãn .
Cho hàm số $y = {\rm{\;}} - {x^3} + \left( {2m + 1} \right){x^2} - \left( {{m^2} - 1} \right)x - 5$ . Với giá trị nào của tham số $m$ thì đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung?
Ta có: $y' = {\rm{\;}} - 3{{\rm{x}}^2} + 2\left( {2m + 1} \right)x - \left( {{m^2} - 1} \right)$
Hàm số có 2 cực trị nằm về 2 phía trục tung$ \Leftrightarrow {\rm{\;}} - 3{{\rm{x}}^2} + 2\left( {2m + 1} \right)x - \left( {{m^2} - 1} \right) = 0$ có hai nghiệm phân biệt trái dấu$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {2m + 1} \right)}^2} - 3\left( {{m^2} - 1} \right) > 0}\\{{m^2} - 1 < 0}\end{array}} \right.$$ \Leftrightarrow {\rm{\;}} - 1 < m < 1$
Biết ${m_0}$ là giá trị của tham số m để hàm số $y = {x^3} - 3{x^2} + mx - 1$ có 2 điểm cực trị ${x_1},{x_2}$ sao cho $x_1^2 + x_2^2 - {x_1}{x_2} = 13$, mệnh đề nào dưới đây đúng?
Xét phương trình $y' = 3{x^2} - 6x + m = 0$ (*). Hàm số có 2 cực trị $ \Leftrightarrow $ Phương trình (*) có $2$ nghiệm phân biệt$ \Leftrightarrow \Delta ' = 9 - 3m > 0 \Leftrightarrow m < 3$
Ta có ${x_1},{x_2}$ là $2$ nghiệm của (*), theo Viét ta có: $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1}{x_2} = \dfrac{m}{3}}\end{array}} \right.$
Khi đó $x_1^2 + x_2^2 - {x_1}{x_2} = 13 $ $\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} = 13$ $ \Leftrightarrow {2^2} - 3.\dfrac{m}{3} = 13$ $ \Leftrightarrow m = - 9$
Vậy $m \in \left( { - 15; - 7} \right)$
Cho hàm số $y = {x^3} + \left( {1 - 2m} \right){x^2} + \left( {2 - m} \right)x + m + 2$. Tập hợp tất cả các giá trị của tham số $m\;$ sao cho hàm số đã cho có $2$ điểm cực trị, đồng thời điểm cực tiểu nhỏ hơn $1$ là
$y = {x^3} + \left( {1 - 2m} \right){x^2} + \left( {2 - m} \right)x + m + 2$$ \Rightarrow y' = 3{x^2} + 2\left( {1 - 2m} \right)x + 2 - m$
Để đồ thị hàm số có 2 điểm cực trị thì $\Delta ' > 0 \Leftrightarrow {\left( {1 - 2m} \right)^2} - 3.\left( {2 - m} \right) > 0$$ \Leftrightarrow 4{m^2} - m - 5 > 0 \Leftrightarrow \left[ \begin{array}{l}m > \dfrac{5}{4}\\m < - 1\end{array} \right.$
Giả sử ${x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} \left( {{x_1} < {\mkern 1mu} {x_2}} \right)$ là nghiệm của phương trình $y' = 0$. Theo Vi – ét: ${x_1} + {x_2} = \dfrac{{4m - 2}}{3},{\mkern 1mu} {\mkern 1mu} {x_1}{x_2} = \dfrac{{2 - m}}{3}$
Do $a = 1 > 0$ nên hàm số đạt cực tiểu tại $x = {x_2}$
Theo đề bài, ta có: điểm cực tiểu nhỏ hơn 1$ \Rightarrow {x_1} < {x_2} < 1$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) > 0}\\{\left( {{x_1} - 1} \right) + \left( {{x_2} - 1} \right) < 0}\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 > 0}\\{\left( {{x_1} + {x_2}} \right) - 2 < 0}\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\dfrac{{2 - m}}{3} - \dfrac{{4m - 2}}{3} + 1 > 0}\\{\dfrac{{4m - 2}}{3} - 2 < 0}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 5m + 7 > 0}\\{4m - 8 < 0}\end{array}} \right. \Leftrightarrow m < \dfrac{7}{5}$
Vậy, để đồ thị của hàm số đã cho có $2$ điểm cực trị, đồng thời điểm cực tiểu nhỏ hơn $1$ thì $m \in \left( { - \infty ; - 1} \right) \cup \left( {\dfrac{5}{4};\dfrac{7}{5}} \right)$.
Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số $y = {x^4} - 2m{x^2} + 2{m^2} - m$ có ba điểm cực trị là ba đỉnh của một tam giác vuông cân?
Ta có:$y' = 4{x^3} - 4mx = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = m}\end{array}} \right.$
Để phương trình có $3$ nghiệm phân biệt \( \Leftrightarrow m > 0\).
$ \Rightarrow y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 2{m^2} - m \Rightarrow A\left( {0;2{m^2} - m} \right)}\\{x = \sqrt m \Rightarrow y = {m^2} - m \Rightarrow B\left( {\sqrt m ;{m^2} - m} \right)}\\{x = - \sqrt m \Rightarrow y = {m^2} - m \Rightarrow C\left( { - \sqrt m ;{m^2} - m} \right)}\end{array}} \right.$
Ta có tam giác $ABC$ luôn là tam giác cân tại $A$ nên để $ABC$ là tam giác vuông cân thì ta cần thêm điều kiện tam giác $ABC$ vuông tại $A.$
$\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0}\\{\overrightarrow {AB} = \left( {\sqrt m ; - {m^2}} \right){\mkern 1mu} ;{\mkern 1mu} \overrightarrow {AC} = \left( { - \sqrt m ; - {m^2}} \right)}\\{ \Rightarrow - m + {m^4} = 0 \Leftrightarrow m\left( {{m^3} - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\\{m = 1{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}} \right.}\end{array}$
Vậy $m = 1.$
Cho hàm số $y = \dfrac{9}{8}{x^4} + 3\left( {m - 3} \right){x^2} + 4m + 2017$ với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều.
Ta có $y' = \dfrac{9}{2}{x^3} + 6\left( {m - 3} \right)x;{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\3{x^2} = 4\left( {3 - m} \right){\rm{ }}\left( * \right)\end{array} \right..$
Để hàm số có ba điểm cực trị $ \Leftrightarrow 4\left( {3 - m} \right) > 0 \Leftrightarrow m < 3.$
Khi đó tọa độ ba điểm cực trị của đồ thị hàm số là:
$A\left( {0;4m + 2017} \right),\,\,B\left( {2\sqrt {\dfrac{{3 - m}}{3}} ;4m + 2017 - 2{{\left( {3 - m} \right)}^2}} \right),\,\,C\left( { - 2\sqrt {\dfrac{{3 - m}}{3}} ;4m + 2017 - 2{{\left( {3 - m} \right)}^2}} \right).$
Do dam giác $ABC$ cân tại $A$ nên yêu cầu bài toán $ \Leftrightarrow A{B^2} = B{C^2}$
$\dfrac{{4\left( {3 - m} \right)}}{3} + 4{\left( {3 - m} \right)^4} = \dfrac{{16\left( {3 - m} \right)}}{3}$$ \Leftrightarrow {\left( {3 - m} \right)^4} = 3 - m$ $ \Leftrightarrow \left[ \begin{array}{l}3 - m = 0\\3 - m = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\left( L \right)\\m = 2\left( {TM} \right)\end{array} \right.$
Tìm tất cả các giá trị thực của tham số \(m\) để đồ thị của hàm số \(y = {x^4} - 2m{x^2}\) có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn $1.$
Ta có $y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m{\rm{ }}\,\left( * \right)\end{array} \right..$
Để hàm số có ba điểm cực trị $ \Leftrightarrow \,\,m > 0.$
Khi đó tọa độ ba điểm cực trị của đồ thị hàm số là: $A\left( {0;0} \right),\,\,B\left( {\sqrt m ; - {m^2}} \right),\,\,C\left( { - \sqrt m ; - {m^2}} \right).$
Tam giác $ABC$ cân tại $A$, suy ra ${S_{\Delta ABC}} = \dfrac{1}{2}d\left( {A,BC} \right).BC$ $ = \dfrac{1}{2}{m^2}.2\sqrt m = {m^2}\sqrt m $.
Theo bài ra, ta có ${S_{\Delta ABC}} < 1 \Leftrightarrow {m^2}\sqrt m < 1$ $ \Leftrightarrow 0 < m < 1\left( {TM} \right)$
Cho hàm số \(y = 3{x^4} + 2\left( {m - 2018} \right){x^2} + 2017\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng \({120^0}\).
Ta có $y' = 12{x^3} + 4\left( {m - 2018} \right)x;{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\3{x^2} = 2018 - m\end{array} \right..$
Để hàm số có ba điểm cực trị $ \Leftrightarrow 2018 - m > 0 \Leftrightarrow m < 2018$.
Khi đó, tọa độ các điểm cực trị của đồ thị hàm số là:
\(A\left( {0;2017} \right),B\left( {\sqrt {\dfrac{{2018 - m}}{3}} ; - \dfrac{{{{\left( {m - 2018} \right)}^2}}}{3} + 2017} \right),C\left( { - \sqrt {\dfrac{{2018 - m}}{3}} ; - \dfrac{{{{\left( {m - 2018} \right)}^2}}}{3} + 2017} \right)\)
Do tam giác $ABC$ cân tại $A$ nên ycbt \( \Leftrightarrow 3A{B^2} = B{C^2}\)
\( \Leftrightarrow 3\left[ {\dfrac{{2018 - m}}{3} + \dfrac{{{{\left( {m - 2018} \right)}^4}}}{9}} \right] = 4\dfrac{{2018 - m}}{3}\)\( \Leftrightarrow {\left( {m - 2018} \right)^3} = - 1 \Leftrightarrow m = 2017\) (thỏa mãn)
Cho hàm số \(y = {x^3} - 3{x^2} - 9x + m\). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
Ta có \(y' = 3{x^2} - 6x - 9;{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \Rightarrow y = 5 + m\\x = 3 \Rightarrow y = - 27 + m\end{array} \right..\)
Suy ra tọa độ hai điểm cực trị là \(A\left( { - 1;5 + m} \right)\) và \(B\left( {3; - 27 + m} \right)\).
Suy ra đường thẳng đi qua hai điểm \(A,{\rm{ }}B\) có phương trình \(y = - 8x + m - 3\).
Cho hàm số \(y = {x^3} - 3{x^2} - mx + 2\) với \(m\) là tham số thực. Tìm giá trị của \(m\) để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng \(d:x + 4y - 5 = 0\) một góc \(\alpha = {45^0}.\)
Ta có \(y' = 3{x^2} - 6x - m.\)
Để đồ thị hàm số đã cho có hai điểm cực trị \( \Leftrightarrow \) phương trình $y' = 0$ có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = 9 + 3m > 0 \Leftrightarrow m > - 3.\)
Ta có \(y = y'.\left( {\dfrac{1}{3}x - \dfrac{1}{3}} \right) - \left( {\dfrac{{2m}}{3} + 2} \right)x + 2 - \dfrac{m}{3}.\)
\( \Rightarrow \) đường thẳng đi qua hai điểm cực trị \(A\) và \(B\) là \(\Delta :y = - \left( {\dfrac{{2m}}{3} + 2} \right)x + 2 - \dfrac{m}{3}.\)
Đường thẳng \(d:x + 4y - 5 = 0\) có một VTPT là \({\vec n_d} = \left( {1;4} \right).\)
Đường thẳng \(\Delta :y = - \left( {\dfrac{{2m}}{3} + 2} \right)x + 2 - \dfrac{m}{3}\) có một VTPT là \({\vec n_\Delta } = \left( {\dfrac{{2m}}{3} + 2;1} \right).\)
Ycbt \( \Leftrightarrow \dfrac{{\sqrt 2 }}{2} = \cos {45^0} = \left| {{\rm{cos}}\left( {{{\vec n}_d},{{\vec n}_\Delta }} \right)} \right| = \dfrac{{\left| {1.\left( {\dfrac{{2m}}{3} + 2} \right) + 4.1} \right|}}{{\sqrt {{1^2} + {4^2}} .\sqrt {{{\left( {\dfrac{{2m}}{3} + 2} \right)}^2} + {1^2}} }}\)
\( \Leftrightarrow 60{m^2} + 264m + 117 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}m = - \dfrac{1}{2}\\m = - \dfrac{{39}}{{10}}\;\end{array} \right. \Rightarrow m = - \dfrac{1}{2}\) (do \(m > - 3\))
Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và hàm số $y = f'\left( x \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
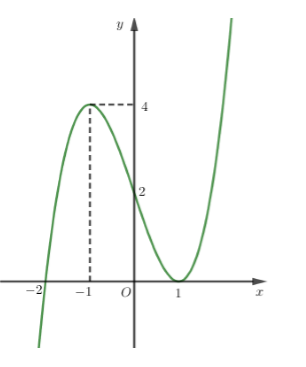
Dựa vào đồ thị hàm số $y = f'\left( x \right)$, ta có các nhận xét sau:
= $f'\left( x \right)$ đổi dấu từ $'' - ''$ sang $'' + ''$ khi đi qua điểm $x = - \,2$ suy ra $x = - \,2$ là điểm cực trị và là điểm cực tiểu của hàm số $y = f\left( x \right).$
= $f'\left( x \right)$ không đổi dấu khi đi qua điểm $x = - \,1,\,\,x = 1$ suy ra $x = - \,1,\,\,x = 1$ không là các điểm cực trị của hàm số $y = f\left( x \right).$
Vậy hàm số đã cho đạt cực tiểu tại điểm $x = - \,2.$
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2017;2018} \right]\) để hàm số $y = \dfrac{1}{3}{x^3} - m{x^2} + \left( {m + 2} \right)x$ có hai điểm cực trị nằm trong khoảng $\left( {0; + \infty } \right)$.
Ta có: $y' = {x^2} - 2mx + m + 2$
Yêu cầu bài toán $ \Leftrightarrow y' = 0$ có hai nghiệm dương phân biệt
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m - 2 > 0\\S = {x_1} + {x_2} > 0\\P = {x_1}{x_2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 1} \right)\left( {m - 2} \right) > 0\\2m > 0\\m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 1\end{array} \right.\\m > 0\end{array} \right. \Leftrightarrow m > 2$
Mà \(m \in \mathbb{Z},m \in \left[ { - 2017;2018} \right] \Rightarrow m = \left\{ {3;4;5;...2018} \right\}\)
Vậy có \(2016\) giá trị.
Cho hàm số $y = - {x^3} + 3m{x^2} - 3m - 1$ với \(m\) là tham số thực. Tìm giá trị của \(m\) để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng $d:x + 8y - 74 = 0$.
Ta có $y' = - 3{x^2} + 6mx = - 3x\left( {x - 2m} \right);{\rm{ }}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right.$.
Để đồ thị hàm số có hai điểm cực trị \( \Leftrightarrow m \ne 0\).
Khi đó gọi $A\left( {0; - 3m - 1} \right)$ và $B\left( {2m;4{m^3} - 3m - 1} \right)$ là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của $AB$ là điểm $I\left( {m;2{m^3} - 3m - 1} \right)$và\(\overrightarrow {AB} = \left( {2m;4{m^3}} \right) = 2m\left( {1;2{m^2}} \right)\).
Đường thẳng \(d\) có một vectơ chỉ phương là \(\overrightarrow u = \left( {8; - 1} \right).\)
Ycbt \( \Leftrightarrow \left\{ \begin{array}{l}I \in d\\\overrightarrow {AB} .\overrightarrow u = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 8\left( {2{m^3} - 3m - 1} \right) - 74 = 0\\8 - 2{m^2} = 0\end{array} \right. \Leftrightarrow m = 2.\)

