Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
Phương trình hoành độ $2{x^2} + 1 = 3x$.
$ \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow y = 3 \hfill \\ x = \dfrac{1}{2} \Rightarrow y = \dfrac{3}{2} \hfill \\ \end{gathered} \right.$
Vậy có hai giao điểm là $\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$.
Số giao điểm của đồ thị hàm số $y = {x^3} - 2{x^2} + x - 1$ và đường thẳng $y = 1 - 2x$ là:
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình:
$\begin{gathered} {x^3} - 2{x^2} + x - 1 = 1 - 2x \Leftrightarrow {x^3} - 2{x^2} + 3x - 2 = 0 \hfill \\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x + 2} \right) = 0 \Leftrightarrow x = 1 \hfill \\ \end{gathered} $
Vậy hai đồ thị hàm số đã cho có $1$ giao điểm duy nhất.
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình:
$\begin{gathered}{x^3} + 2{x^2} - x + 1 = {x^2} - x + 3 \Leftrightarrow {x^3} + {x^2} - 2 = 0 \hfill \\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 2x + 2} \right) = 0 \Leftrightarrow x = 1 \hfill \\ \end{gathered} $
Như vậy hai đồ thị có $1 $ điểm chung.
Các đồ thị hàm số $y = {x^4} - 2{x^2} + 2$ và $y = - {x^2} + 4$ có tất cả bao nhiêu điểm chung?
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
$\begin{gathered}{x^4} - 2{x^2} + 2 = - {x^2} + 4 \Leftrightarrow {x^4} - {x^2} - 2 = 0 \hfill \\ \Leftrightarrow \left[ \begin{gathered} {x^2} = - 1 < 0(L) \hfill \\ {x^2} = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow x = \pm \sqrt 2 \hfill \\ \end{gathered} $
Như vậy hai đồ thị có $2$ giao điểm.
Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:
Phương trình hoành độ giao điểm: $3{x^2} = {x^3} + {x^2} + x + 1 \Leftrightarrow {x^3} - 2{x^2} + x + 1 = 0$.
Xét hàm $f\left( x \right) = {x^3} - 2{x^2} + x + 1$ ta có:
$f'\left( x \right) = 3{x^2} - 4x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow f\left( 1 \right) = 1 \hfill \\ x = \dfrac{1}{3} \Rightarrow f\left( {\dfrac{1}{3}} \right) = \dfrac{{31}}{{27}} \hfill \\ \end{gathered} \right.$
Bảng biến thiên:
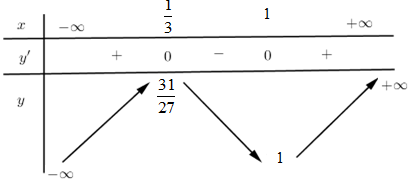
Từ bảng biến thiên ta thấy đường thẳng $y = 0$ chỉ cắt đồ thị hàm số tại $1$ điểm duy nhất nên hai đồ thị hàm số cắt nhau tại duy nhất $1$ điểm.
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ và đường thẳng d: $y = - m$.
Xét hàm số (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ có: $y' = 5{x^4} + 3{x^2} + \dfrac{1}{{2\sqrt {1 - x} }} > 0\,\,\forall x \in \left( { - \infty ;1} \right)$$ \Rightarrow $ hàm số luôn đồng biến trên $\left( { - \infty ;1} \right]$.
Lại có $y\left( 1 \right) = 2$.
Ta có BBT:
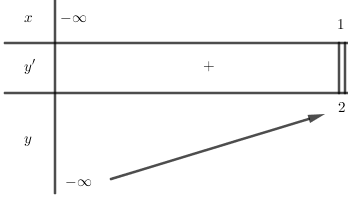
Theo BBT ta thấy pt có nghiệm $ \Leftrightarrow - m \leqslant 2 \Leftrightarrow m \geqslant - 2$.
Cho hàm số $y = {x^3} + 3{x^2} + m$ có đồ thị $\left( C \right)$.Để đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A,B,C$ sao cho $C$ là trung điểm của $AB$ thì giá trị của tham số $m$ là:
Vì đồ thị của hàm đa thức bậc 3 luôn có tâm đối xứng $I\left( {{x_0};{y_0}} \right)$ có hoành độ ${x_0}$ là nghiệm của phương trình $y''\left( {{x_0}} \right) = 0$
Vậy đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A, B, C$ sao cho $C$ là trung điểm $AB$
$ \Leftrightarrow $$C$ là tâm đối xứng của $\left( C \right)$
Ta có:
$y' = 3{x^2} + 6x \Rightarrow y'' = 6x + 6 = 0 \Leftrightarrow x = - 1 \Rightarrow y = m + 2 \Rightarrow C\left( { - 1;m + 2} \right)$$C \in Ox \Leftrightarrow y = 0 \Leftrightarrow m + 2 = 0 \Leftrightarrow m = - 2$
Biết đường thẳng $y = mx + 1$ cắt đồ thị hàm số $y = {x^3} - 3x + 1$ tại ba điểm phân biệt. Tất cả các giá trị thực của tham số $m$ là:
Xét phương trình hoành độ giao điểm $mx + 1 = {x^3} - 3x + 1$
$ \Leftrightarrow {x^3} - 3x - mx = 0 \Leftrightarrow x\left( {{x^2} - 3 - m} \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ {x^2} = m + 3\left( * \right) \hfill \\ \end{gathered} \right.$
Để đường thẳng cắt đồ thị hàm số tại $3$ điểm phân biệt thì $\left( * \right)$ phải có hai nghiệm phân biệt khác $0$ $ \Leftrightarrow m + 3 > 0 \Leftrightarrow m > - 3$.
Cho hàm số $y = {x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right)$. Tập hợp tất cả các giá trị của $m$ để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
${x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right) = 0$
$ \Leftrightarrow \left( {x + 1} \right)\left[ {{x^2} - \left( {m + 4} \right)x + 3\left( {m + 1} \right)} \right] = 0 \Leftrightarrow \left[ \begin{gathered} x = - 1 \hfill \\{x^2} - \left( {m + 4} \right)x + 3\left( {m + 1} \right) = 0\left( * \right) \hfill \\ \end{gathered} \right. $
Để đồ thị hàm số cắt trục hoành tại $3$ điểm phân biệt có hoành độ âm thì phương trình $\left( * \right)$ có 2 nghiệm âm phân biệt khác $ - 1$
$ \Leftrightarrow \left\{ \begin{gathered} \Delta > 0 \hfill \\ - \dfrac{b}{a} < 0 \hfill \\ \dfrac{c}{a} > 0 \hfill \\ y\left( { - 1} \right) \ne 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} {\left( {m - 2} \right)^2} > 0 \hfill \\ m + 4 < 0 \hfill \\ 3\left( {m + 1} \right) > 0 \hfill \\ {\left( { - 1} \right)^2} - \left( {m + 4} \right)\left( { - 1} \right) + 3\left( {m + 1} \right) \ne 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} m \ne 2 \hfill \\ m < - 4 \hfill \\ m > - 1 \hfill \\ m \ne - 2 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow m \in \emptyset $
Gọi \(S\) là tập các số nguyên \(m \in [ - 5;5]\) để phương trình \(2x - 2\sqrt {x - \sqrt {{x^2} - 4} } \)\( + \sqrt {x + \sqrt {{x^2} - 4} } \)\( = 2m + 2\sqrt {{x^2} - 4} \) có nghiệm. Số tập con của tập \(S\) là
Bước 1: Tìm điều kiện xác định.
Điều kiện xác định \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 4 \ge 0}\\{x - \sqrt {{x^2} - 4} \ge 0 \Leftrightarrow x \ge 2}\\{x + \sqrt {{x^2} - 4} \ge 0}\end{array}} \right.\)
Bước 2: Đặt \(t = \sqrt {x - \sqrt {{x^2} - 4} } (0 < t \le \sqrt 2 )\)
Nhận xét: \(\sqrt {x - \sqrt {{x^2} - 4} } \cdot \sqrt {x + \sqrt {{x^2} - 4} } = 2\).
Đặt \(t = \sqrt {x - \sqrt {{x^2} - 4} } (0 < t \le \sqrt 2 )\). Phương trình trên trở thành:
\(2{t^2} - 2t + \dfrac{2}{t} = 2m\)\( \Leftrightarrow {t^2} - t + \dfrac{1}{t} = m\)
Bước 3: Xét hàm số \(f(t) = {t^2} - t + \dfrac{1}{t}\), lập bảng biến thiên
Xét hàm số \(f(t) = {t^2} - t + \dfrac{1}{t}\), với \(0 < t \le \sqrt 2 \).
Do đó \({f^\prime }(t) = 2t - 1 - \dfrac{1}{{{t^2}}},\)
\({f^\prime }(t) = 0 \Leftrightarrow t = 1\).
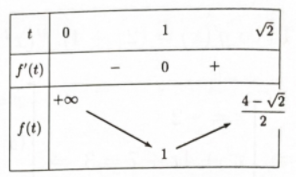
Bước 4: Tìm số tập con của tập hợp \(S\)
Dựa vào bảng biến thiên, để phương trình có nghiệm thì \(m \ge 1\).
Vì \(m \in \mathbb{Z}\) và \(m \in [ - 5;5]\) nên ta có \(S = \{ 1;2;3;4;5\} \).
Vậy số tập con của tập hợp \(S\) là \({2^5} = 32\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
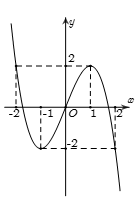
Đáp án A: đúng.
Đáp án B: Với \(m > 2\) hoặc \(m < - 2\) thì đường thẳng \(y = m\) cắt đồ thị hàm số tại một điểm duy nhất nên B đúng.
Đáp án C: Hàm số đạt cực tiểu tại \(x = - 1\) chứ không phải đạt cực tiểu bằng \( - 1\) nên C sai.
Đáp án D: Giá trị lớn nhất của hàm số trên \(\left[ { - 2;2} \right]\) đạt được bằng \(2\) tại \(x = - 2\) nên D đúng.
Đề thi THPT QG - 2021 - mã 103
Đồ thị của hàm số \(y = - {x^3} + 2{x^2} - 1\) cắt trục tung tại điểm có tung độ bằng:
Đồ thị hàm số \(y = - {x^3} + 2{x^2} - 1\) cắt trục tung \( \Rightarrow x = 0\)
Với \(x = 0\) thay vào hàm số \( \Rightarrow y = - 1\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(|\sin x - \cos x| + \) \(4\sin 2x = m\) có nghiệm thực?
Đặt \(t = |\sin x - \cos x|\)\( = \sqrt 2 \left| {\sin \left( {x - \dfrac{\pi }{4}} \right)} \right| \in [0;\sqrt 2 ]\)
\( \Rightarrow {t^2} = 1 - \sin 2x \Leftrightarrow \sin 2x = 1 - {t^2}.\)
Phương trình đã cho trở thành \(t + 4\left( {1 - {t^2}} \right) = m\)\( \Leftrightarrow - 4{t^2} + t + 4 = m(*)\)
Phương trình đã cho có nghiệm thực \( \Leftrightarrow \) Phương trình \((*)\) có nghiệm thực trên \([0;\sqrt 2 ]\).
Xét hàm số \(f(t) = - 4{t^2} + t + 4\) trên \([0;\sqrt 2 ]\).
Ta có \({f^\prime }(t) = - 8t + 1\).
\( \Rightarrow {f^\prime }(t) = 0 \Leftrightarrow - 8t + 1 = 0\)\( \Leftrightarrow t = \dfrac{1}{8}\)
Ta có bảng biến thiên
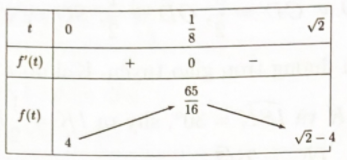
Dựa vào bảng biến thiên ta có yêu cầu bài toán \( \Leftrightarrow \sqrt 2 - 4 \le m \le \dfrac{{65}}{{16}}\).
Do \(m \in \mathbb{Z} \Rightarrow m \in \{ - 2; - 1;0;1;2;3;4\} \). Vậy có 7 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
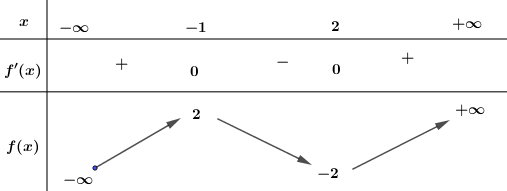
Số nghiệm thực của phương trình \(2f\left( x \right) + 3 = 0\) là
\(2f\left( x \right) + 3 = 0 \Leftrightarrow f\left( x \right) = - \dfrac{3}{2} \Rightarrow \) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - \dfrac{3}{2}\) song song với trục hoành.
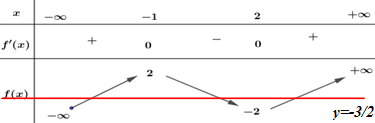
Dựa vào BBT ta thấy đường thẳng \(y = - \dfrac{3}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt.
Vậy phương trình \(2f\left( x \right) + 3 = 0\) có 3 nghiệm phân biệt.
Có tất cả bao nhiêu số nguyên \(m\) thỏa mãn đồ thị hàm số \(y = {x^3} + 2020x + m\) và trục hoành có duy nhất một điểm chung?
Đồ thị hàm số \(y = {x^3} + 2020x + m\) và trục hoành có duy nhất 1 điểm chung
\( \Leftrightarrow \) Phương trình hoành độ giao điểm của hai đồ thị hàm số \({x^3} + 2020x + m = 0\) \( \Leftrightarrow {x^3} + 2020x = - m\) có nghiệm duy nhất
\( \Leftrightarrow \) Đường thẳng \(y = - m\) và đồ thị hàm số \(y = {x^3} + 2020x\) có duy nhất 1 điểm chung.
Xét hàm số \(y = {x^3} + 2020x\) ta có: \(y' = 3{x^2} + 2020 > 0\,\,\forall x\)
\( \Rightarrow \) Hàm số \(y = {x^3} + 2020x\) đồng biến trên \(\mathbb{R}.\)
Ta có BBT:
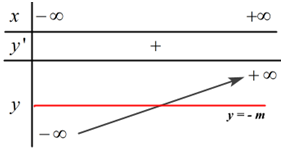
\( \Rightarrow \) Với mọi giá trị của \(m\) thì đường thẳng \(y = - m\) luôn cắt đồ thị hàm số \(y = {x^3} + 2020x\) tại duy nhất 1 điểm.
Vậy có vô số giá trị của \(m\) thỏa mãn bài toán.
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là:
+ Để giải phương trình \(f\left( {f\left( x \right)} \right) = 0\) ta đi xét phương trình \(f\left( x \right) = 0\).
Từ đồ thị \(f\left( x \right)\) kẻ tương giao với đường thẳng \(y = 0 \Rightarrow \) Phương trình \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\,voi\,\,a < - 1\\x = b\,\,voi\,\,b \in \left( { - 1;0} \right)\\x = c\,\,voi\,\,c \in \left( {0;1} \right)\\x = d\,\,voi\,\,d > 1\end{array} \right.\).
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a \to ke\,\,tuong\,\,giao\,\,\left( {a < - 1} \right) \Rightarrow 0\,\,nghiem\\f\left( x \right) = b \to ke\,\,tuong\,\,giao\,\,\left( {b \in \left( { - 1;0} \right)} \right) \Rightarrow 4\,\,nghiem\\f\left( x \right) = c \to ke\,\,tuong\,\,giao\,\,\left( {c \in \left( {0;1} \right)} \right) \Rightarrow 4\,\,nghiem\\f\left( x \right) = d \to ke\,\,tuong\,\,giao\,\,\left( {d > 1} \right) \Rightarrow 2\,\,nghiem\end{array} \right.\)
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 1\) có 10 nghiệm phân biệt.
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
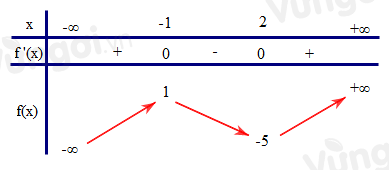
Số nghiệm thực phân biệt của phương trình \({f^\prime }(f(x)) = 0\) là
Xét phương trình \({f^\prime }(f(x)) = 0\) (1)
Đặt \(t = f(x)\)
\((1) \Leftrightarrow {f^\prime }(t) = 0\)
Dựa vào bảng biến thiên của hàm số \(y = f(x)\)
Ta có \({f^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{x = 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 2}\end{array}} \right.} \right.\)
Với \(t = - 1 \Leftrightarrow f(t) = - 1 \Leftrightarrow f(x) = - 1 \Rightarrow 3\) nghiệm
Với \(t = 2 \Leftrightarrow f(t) = 2 \Leftrightarrow f(x) = 2 \Rightarrow 1\) nghiệm
Vậy số nghiệm thực phân biệt của phương trình là \(3 + 1 = 4\) nghiệm.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên.
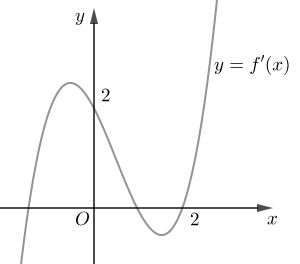
Bất phương trình \(f\left( x \right) > 2x + m\) (\(m\) là tham số thực) nghiệm đúng với mọi \(x \in \left( {0;2} \right)\) khi và chỉ khi
\(f\left( x \right) > 2x + m \Leftrightarrow m < f\left( x \right) - 2x = g\left( x \right)\,\,\forall x \in \left( {0;2} \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {0;2} \right]} g\left( x \right)\).
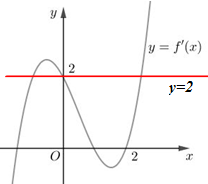
Ta có \(g'\left( x \right) = f'\left( x \right) - 2 = 0 \Leftrightarrow f'\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} < 0\\x = 0\\x = {x_2} > 2\end{array} \right.\).
Từ đó ta có BBT của đồ thị hàm số \(y = g\left( x \right) = f\left( x \right) - 2\) như sau:
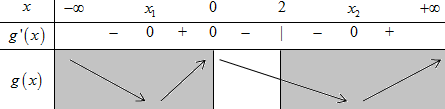
Xét trên \(\left[ {0;2} \right]\) ta thấy \(\mathop {\min }\limits_{\left[ {0;2} \right]} g\left( x \right) = g\left( 2 \right) = f\left( 2 \right) - 2.2 = f\left( 2 \right) - 4\).
Vậy \(m \le f\left( 2 \right) - 4\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
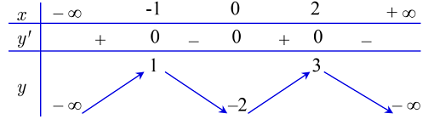
Số nghiệm thực của phương trình \(2f\left( x \right) + 5 = 0\) là:
Số nghiệm của phương trình \(2f\left( x \right) + 5 = 0\) \( \Leftrightarrow f\left( x \right) = - \dfrac{5}{2}\) là số giao điểm của đường thẳng \(y = - \dfrac{5}{2}\) và đồ thị hàm số \(y = f\left( x \right).\)
Ta có BBT:
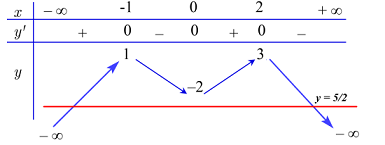
Dựa vào BBT ta thấy đường thẳng \(y = - \dfrac{5}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt.
\( \Rightarrow 2f\left( x \right) + 5 = 0\) có 2 nghiệm phân biệt.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
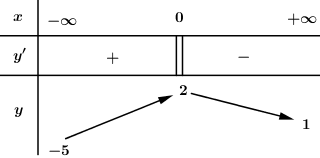
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = m\) có nghiệm duy nhất?
Phương trình \(f\left( x \right) = m\) là có nghiệm duy nhất \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất.
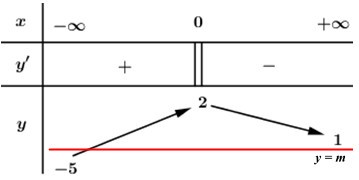
Dựa vào BBT ta thấy, đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất \( \Leftrightarrow \left[ \begin{array}{l} - 5 < m \le 1\\m = 2\end{array} \right.\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;\,\,0;\,\,1;\,\,2} \right\}\)
Vậy có 7 giá trị nguyên của m thỏa mãn bài toán.
