Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
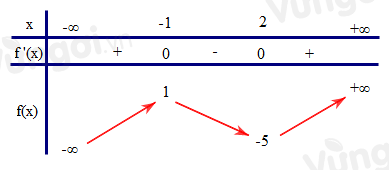
Số nghiệm thực phân biệt của phương trình \({f^\prime }(f(x)) = 0\) là
Trả lời bởi giáo viên
Xét phương trình \({f^\prime }(f(x)) = 0\) (1)
Đặt \(t = f(x)\)
\((1) \Leftrightarrow {f^\prime }(t) = 0\)
Dựa vào bảng biến thiên của hàm số \(y = f(x)\)
Ta có \({f^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{x = 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 2}\end{array}} \right.} \right.\)
Với \(t = - 1 \Leftrightarrow f(t) = - 1 \Leftrightarrow f(x) = - 1 \Rightarrow 3\) nghiệm
Với \(t = 2 \Leftrightarrow f(t) = 2 \Leftrightarrow f(x) = 2 \Rightarrow 1\) nghiệm
Vậy số nghiệm thực phân biệt của phương trình là \(3 + 1 = 4\) nghiệm.
Hướng dẫn giải:
- Đặt \(t = f(x)\)
- Giải phương trình f’(x)=0
- Tìm t rồi tìm x.

