Trả lời bởi giáo viên
Đáp án đúng: b
Phương trình hoành độ giao điểm: 3x2=x3+x2+x+1⇔x3−2x2+x+1=0.
Xét hàm f(x)=x3−2x2+x+1 ta có:
f′(x)=3x2−4x+1=0⇔[x=1⇒f(1)=1x=13⇒f(13)=3127
Bảng biến thiên:
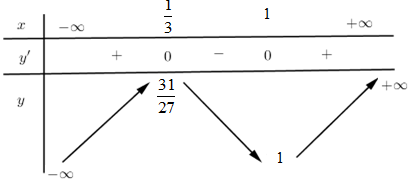
Từ bảng biến thiên ta thấy đường thẳng y=0 chỉ cắt đồ thị hàm số tại 1 điểm duy nhất nên hai đồ thị hàm số cắt nhau tại duy nhất 1 điểm.
Hướng dẫn giải:
- Bước 1: Lập phương trình hoành độ giao điểm .
- Bước 2: Khảo sát sự biến thiên của hàm số h(x)=f(x)−g(x) trên TXĐ.
+ Tính h′(x), giải phương trình h′(x)=0 tìm các nghiệm và các điểm h′(x) không xác định.
+ Xét dấu h′(x) và lập bảng biến thiên.
- Bước 3: Kết luận số giao điểm của hai đồ thị hàm số y=f(x) và y=g(x).
+ Số giao điểm của hai đồ thị hàm số y=f(x) và y=g(x) là số giao điểm của đồ thị hàm số h(x) với trục hoành (đường thẳng y=0)
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
