Phương trình x3−3x2+m=0 có ba nghiệm phân biệt khi và chỉ khi m thuộc khoảng
Bước 1:
Ta có: x3−3x2=−m
Bước 2:
Đặt y=f(x)=x3−3x2 , ta có: f′(x)=3x2−6x=0⇔[x=0x=2
BBT của hàm số f(x)=x3−3x2
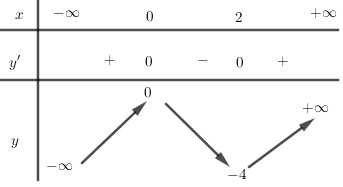
Bước 3:
Đường thẳng y=−m cắt đồ thị hàm số f(x)=x3−3x2 tại ba điểm phân biệt khi −4<−m<0⇔0<m<4
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số bậc ba y=f(x)có đồ thị như hình vẽ bên.
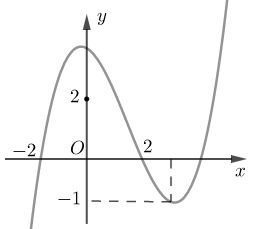
Số nghiệm thực của phương trình |f(x3−3x)|=23 là
|f(x3−3x)|=23⇔[f(x3−3x)=23(∗)f(x3−3x)=−23(∗∗)
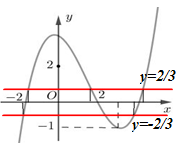
Pt(∗)⇔[x3−3x=x1(−2<x1<0)(1)x3−3x=x2(0<x2<2)(2)x3−3x=x3(x3>2)(3)
Pt(∗∗)⇔[x3−3x=x4(x4<−2)(4)x3−3x=x5(x5>2)(5)x3−3x=x6(x6>2)(6)
Xét phương trình g(x)=x3−3x=xi, số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=g(x) và đường thẳng y=xi song song với trục hoành.
Ta có g′(x)=3x2−3=0⇔x=±1.
BBT:
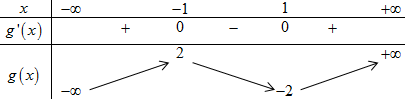
Từ BBT ta thấy:
(1), (2) có 3 nghiệm phân biệt.
(3), (4), (5), (6) có 1 nghiệm.
Và dễ thấy tất cả các nghiệm trên là không trùng nhau.
Vậy phương trình ban đầu có 10 nghiệm phân biệt.
Gọi T là tập hợp tất cả các giá trị nguyên của tham số m để phương trình x3−3x2−m3+3m2=0 có ba nghiệm phân biệt. Tổng tất cả các phần tử của T bằng
Ta có:
x3−3x2−m3+3m2=0⇔(x3−m3)−3(x2−m2)=0⇔(x−m)(x2+mx+m2)−3(x−m)(x+m)=0⇔(x−m)(x2+mx+m2−3x−3m)=0⇔(x−m)[x2+(m−3)x+m2−3m]=0⇔[x−m=0x2+(m−3)x+m2−3m=0⇔[x=mx2+(m−3)x+m2−3m=0(1)
Đặt f(x)=x2+(m−3)x+m2−3m.
Để pt đã cho có 3 nghiệm phân biệt thì (1) có 2 nghiệm phân biệt khác m⇔{Δ>0f(m)≠0
⇔{(m−3)2−4(m2−3m)>0m2+(m−3).m+m2−3m≠0⇔{(m−3)2−4m(m−3)>0m2+m2−3m+m2−3m≠0⇔{(m−3)(m−3−4m)>03m2−6m≠0⇔{(m−3)(−3m−3)>03m(m−2)≠0⇔{−1<m<3m≠0,m≠2
Do m∈Z nên m=1 hay T={1}.
Vậy tổng các phần tử của T là 1.
Đồ thị hàm số y=13x4−3x2−2020 cắt trục hoành tại bao nhiêu điểm?
Xét phương trình hoành độ giao điểm 13x4−3x2−2020=0 (*)
Đặt x2=t≥0 ta có phương trình 13t2−3t−2020=0
Phương trình trên có ac=13.(−2020)<0 nên có hai nghiệm trái dấu t1<0<t2
Suy ra x2=t2⇔x=±√t2
Hay phương trình (*) có hai nghiệm phân biệt nên đồ thị hàm số đã cho cắt trục hoành tại 2 điểm phân biệt.
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số y=x−2x−1+x−1x+xx+1+x+1x+2 và y=|x+1|−x−m (m là tham số thực) có đồ thị lần lượt là (C1)và (C2). Tập hợp tất cả các giá trị của m để (C1) và (C2) cắt nhau tại đúng bốn điểm phân biệt là:
Xét phương trình hoành độ giao điểm
x−2x−1+x−1x+xx+1+x+1x+2=|x+1|−x−m
⇔x−2x−1+x−1x+xx+1+x+1x+2−|x+1|+x=−m.
Xét hàm số f(x)=x−2x−1+x−1x+xx+1+x+1x+2−|x+1|+x có TXĐ D=R∖{−2;−1;0;1}.
f′(x)=1(x−1)2+1x2+1(x+1)2+1(x+2)2−x+1|x+1|+1
Ta có −x+1|x+1|+1=|x+1|−(x+1)|x+1|.
Do |x+1|≥x+1∀x⇒|x+1|−(x+1)≥0⇔|x+1|−(x+1)|x+1|≥0.
⇒f′(x)>0∀x∈D
⇒Hàm số đồng biến trên từng khoảng xác định của nó.
Bảng biến thiên:

Từ BBT ta thấy phương trình f(x)=−m có đúng 4 nghiệm phân biệt khi và chỉ khi −m≥3⇔m≤−3
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ. Số nghiệm thực của phương trình 4f(x)−7=0 là:
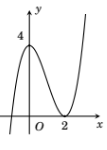
Số nghiệm của phương trình 4f(x)−7=0⇔f(x)=74 là số giao điểm của đường thẳng y=74 và đồ thị (C) của hàm số y=f(x).
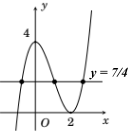
Dựa vào đồ thị hàm số ta thấy đường thẳng y=74 cắt đồ thị hàm số (C):y=f(x) tại 3 điểm phân biệt.
⇒ Phương trình đã cho có 3 nghiệm phân biệt.
Cho hàm số y=(x−2)(x2+1) có đồ thị (C). Mệnh đề nào dưới đây đúng?
Xét phương trình hoành độ giao điểm (x−2)(x2+1)=0⇔x−2=0⇔x=2 (do x2+1>0∀x).
Vậy (C) cắt trục hoành tại một điểm.
Cho hàm số y=f(x) có bảng biến thiên:
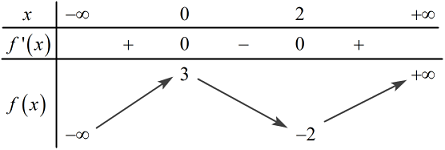
Số nghiệm của phương trình 2f(x)−3=0 là:
Số nghiệm của phương trình 2f(x)−3=0⇔f(x)=32 là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y=32
Ta có BBT:
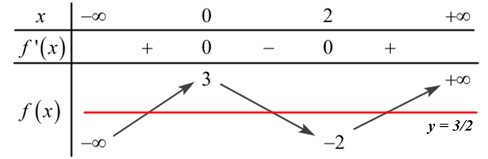
Dựa vào BBT ta thấy đường thẳng y=32 cắt đồ thị hàm số y=f(x) tại 3 điểm phân biệt
⇒ Phương trình 2f(x)−3=0 có 3 nghiệm phân biệt.
Cho hàm số f(x) có đồ thị trong hình bên. Phương trình f[f(cosx)−1]=0 có bao nhiêu nghiệm thuộc đoạn [0;2π]?
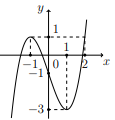
Đặt t=f(cosx)−1, phương trình trở thành f(t)=0.
Dựa vào đồ thị hàm số ta thấy f(t)=0⇔[t=a∈(−2;−1)t=b∈(−1;0)t=c∈(1;2)
Khi đó ta có: [f(cosx)−1=a∈(−∞;−1)f(cosx)−1=b∈(−1;0)f(cosx)−1=c∈(1;2)⇒[f(cosx)=a+1∈(−1;0)(1)f(cosx)=b+1∈(0;1)(2)f(cosx)=c+1∈(2;3)(3)
Tiếp tục dựa vào đồ thị hàm số ta có:
(1)⇔[cosx=a1<−1(1.1)cosx=a2∈(−1;0)(1.2)cosx=a3>1(1.3)
Các phương trình (1.1), (1.3) vô nghiệm do −1≤cosx≤1, phương trình (1.2) có 2 nghiệm phân biệt thuộc [0;2π].
(2)⇔[cosx=b1<−1(2.1)cosx=b2∈(−1;0)(2.2)cosx=b3>1(2.3)
Các phương trình (1.1), (1.3) vô nghiệm do −1≤cosx≤1, phương trình (1.2) có 2 nghiệm phân biệt thuộc [0;2π].
(3)⇔cosx=c1>1⇒ Phương trình vô nghiệm.
Vậy phương trình ban đầu có 4 nghiệm phân biệt thuộc [0;2π].
Cho hàm số f(x) liên tục trên R∖{0} và có bảng biến thiên dưới đây.
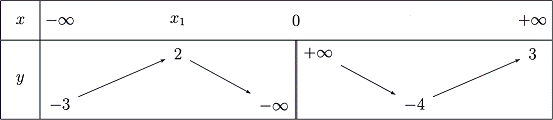
Số nghiệm của phương trình f(x)=5 là
Nghiệm của phương trình f(x)=5 là số giao điểm của đường thẳng y=5 và đồ thị hàm số.
Dựa vào bảng biến thiên ta thấy đường thẳng y=5>3 cắt đồ thị hàm số tại 1 điểm.
Vậy phương trình f(x)=5 có duy nhất 1 nghiệm.
Cho hàm số y=f(x) có đồ thị trong hình sau:
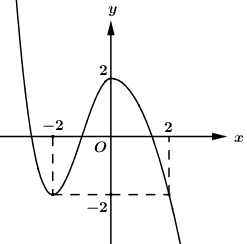
Số nghiệm của phương trình f(x3−3x)+1=0 trong khoảng (0;2) là:
Đặt t=x3−3x ta có t′=3x2−3=0⇔[x=1∈(0;2)x=−1∉(0;2).
Ta có BBT:
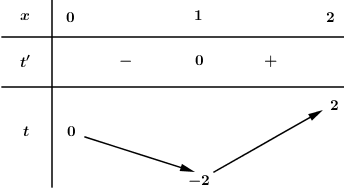
Suy ra x∈(0;2) thì t∈[−2;2).
Khi đó phương trình trở thành f(t)+1=0⇔f(t)=−1.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=−1.
Dựa vào đồ thị hàm số ta thấy đường thẳng y=−1 cắt đồ thị hàm số y=f(t) tại 3 điểm phân biệt, do đó phương trình f(t)=−1 có 3 nghiệm phân biệt [t=a∈(−∞;−2)(ktm)t=b∈(−2;0)t=c∈(0;2).
Dựa vào BBT hàm số t=x3−3x ta có:
+ Phương trình t=b∈(−2;0) có 2 nghiệm phân biệt.
+ Phương trình t=c∈(0;2) có 1 nghiệm duy nhất.
Vậy phương trình đã cho có tất cả 3 nghiệm.
Cho hàm số f(x) có bảng biến thiên sau
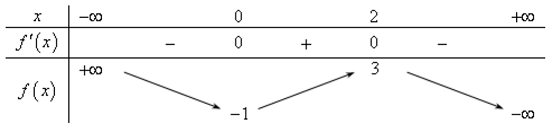
Tìm tất cả các giá trị của tham số m để phương trình f(2tanx)=2m+1 có nghiệm thuộc khoảng (0;π4)?
Đặt t=2tanx, với x∈(0;π4) thì tanx∈(0;1)⇒t∈(0;2).
Khi đó phương trình trở thành: f(t)=2m+1, số nghiệm của phương trình f(t)=2m+1 là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=2m+1 song song với trục hoành.
Quan sát BBT trên khoảng (0;2), ta thấy, phương trình có nghiệm ⇔−1<2m+1<3⇔−1<m<1.
Cho hàm số bậc bốn y=f(x) có đồ thị như hình bên. Hỏi phương trình |f(x)|=1 có bao nhiêu nghiệm?
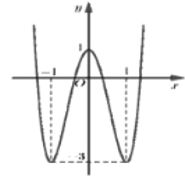
Ta có: |f(x)|=1⇔[f(x)=1(1)f(x)=−1(2).
+ Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số y = f\left( x \right) và đường thẳng y = 1, suy ra phương trình (1) có 3 nghiệm phân biệt.
+ Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số y = f\left( x \right) và đường thẳng y = - 1, suy ra phương trình (2) có 4 nghiệm phân biệt.
Dễ thấy các nghiệm trên không có nghiệm nào trùng nhau.
Vậy phương trình đã cho có 7 nghiệm phân biệt.
Có bao nhiêu giá trị nguyên dương của m để phương trình \left| {{x^3} - 3{x^2} + 2} \right| = m có đúng 6 nghiệm thực phân biệt.
Số nghiệm của phương trình \left| {{x^3} - 3{x^2} + 2} \right| = m là số giao điểm của đồ thị hàm số y = \left| {{x^3} - 3{x^2} + 2} \right| và đường thẳng y = m song song với trục hoành.
Xét hàm số y = {x^3} - 3{x^2} + 2 ta có:
+ TXĐ: D = \mathbb{R}.
+ y' = 3{x^2} - 6x, y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..
+ \left\{ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y = - 2\end{array} \right.
Ta vẽ được đồ thị hàm số y = {x^3} - 3{x^2} + 2 như sau:
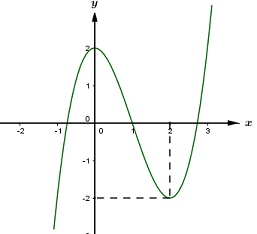
Từ đó ta vẽ được đồ thị hàm số y = \left| {{x^3} - 3{x^2} + 2} \right| như sau:
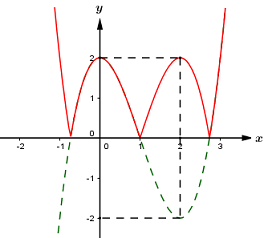
(Đường màu đỏ)
Dựa vào đồ thị hàm số ta thấy phương trình \left| {{x^3} - 3{x^2} + 2} \right| = m có 6 nghiệm phân biệt khi và chỉ khi 0 < m < 2.
Mà m nguyên dương \Rightarrow m = 1.
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hàm số y = f\left( x \right) có bảng biến thiên như sau:
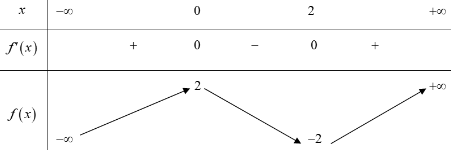
Số nghiệm thực của phương trình f\left( x \right) = f\left( 2 \right) là:
Dựa vào bảng biến thiên ta thấy f\left( 2 \right) = - 2.
Số nghiệm của phương trình f\left( x \right) = f\left( 2 \right) là số giao điểm của đồ thị hàm số y = f\left( x \right) và đường thẳng y = f\left( 2 \right) = - 2.
Dựa vào BBT ta thấy đường thẳng y = - 2 cắt đồ thị hàm số y = f\left( x \right) tại 2 điểm phân biệt.
Vậy phương trình f\left( x \right) = f\left( 2 \right) có hai nghiệm phân biệt.
Cho hàm số y = f\left( x \right) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình f\left( {x + 2019} \right) = 1 là:
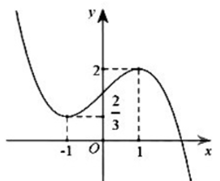
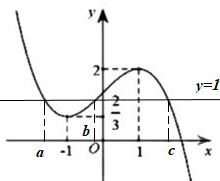
Dựa vào đồ thị hàm số ta thấy: Đường thẳng y = 1 cắt đồ thị hàm số y = f\left( x \right) tại 3 điểm phân biệt nên phương trình f\left( {x + 2019} \right) = 1 có 3 nghiệm phân biệt \left[ \begin{array}{l}x + 2019 = a\\x + 2019 = b\\x + 2019 = c\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = a - 2019\\x = b - 2019\\x = c - 2019\end{array} \right..
Cho hàm số f\left( x \right) có bảng biến thiên như sau:
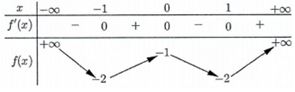
Số nghiệm thuộc đoạn \left[ { - \pi ;2\pi } \right] của phương trình 2f\left( {\sin x} \right) + 3 = 0 là:
Phương trình 2f\left( {\sin x} \right) + 3 = 0 \Leftrightarrow f\left( {\sin x} \right) = - \dfrac{3}{2}\,\,\,\,\left( * \right) có nghiệm trên \left[ { - \pi ;\,\,2\pi } \right] \Leftrightarrow đường thẳng y = - \dfrac{3}{2} cắt đồ thị hàm số y = f\left( {\sin x} \right) tại các điểm trên \left[ { - \pi ;\,\,2\pi } \right].
Đặt \sin x = t \Rightarrow x \in \left[ { - \pi ;\,\,2\pi } \right] \Rightarrow t \in \left[ { - 1;\,\,1} \right].
Ta có BBT:
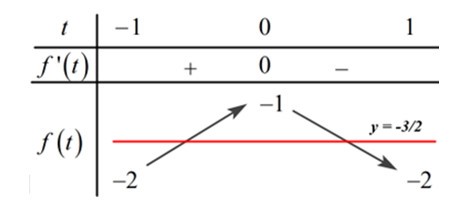
Dựa vào BBT ta có: đường thẳng y = - \frac{3}{2} cắt đồ thị hàm số y = f\left( t \right) tại hai điểm phân biệt.
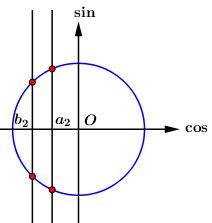
Ta có \left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sin x = {t_1} \in \left( {0;1} \right)\\\sin x = {t_2} \in \left( { - 1;0} \right)\end{array} \right..
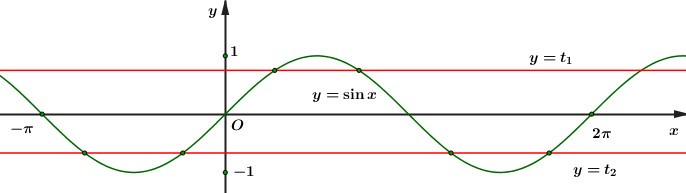
Dựa vào đồ thị hàm số ta thấy:
+) Đường thẳng y = {t_1} cắt đồ thị hàm số y = \sin x tại hai điểm phân biệt trong \left[ { - \pi ;\,\,2\pi } \right].
+) Đường thẳng y = {t_2} cắt đồ thị hàm số y = \sin x tại bốn điểm phân biệt trong \left[ { - \pi ;\,\,2\pi } \right].
Như vậy đường thẳng y = - \frac{3}{2} cắt đồ thị hàm số y = f\left( {\sin x} \right) tại 6 điểm phân biệt trên \left[ { - \pi ;\,\,2\pi } \right].
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số y = - 2{x^3} + 3{x^2} - 5 cắt trục tung tại điểm có tung độ bằng
Ta có đồ thị của hàm số y = - 2{x^3} + 3{x^2} - 5 cắt trục tung tại điểm có tung độ y = - 5
Cho hàm số y = f\left( x \right) có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình f\left( {3 - \sqrt {4 - {x^2}} } \right) = m có hai nghiệm phân biệt thuộc đoạn \left[ { - \sqrt 2 ;\sqrt 3 } \right]. Tìm tập S.
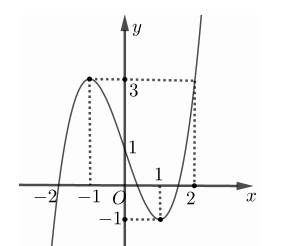
Đặt t = 3 - \sqrt {4 - {x^2}} \Rightarrow 3 - t = \sqrt {4 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = 4 - {\left( {3 - t} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = \left( {t - 1} \right)\left( {5 - t} \right) \ge 0\end{array} \right. \Rightarrow 1 \le t \le 3
Nhận thấy với t = 1 thì {x^2} = 0 \Leftrightarrow x = 0 hay với t = 1 thì ta chỉ tìm được đúng một nghiệm x (loại)
Với 1 < t \le 3 thì {x^2} > 0 nên ta sẽ tìm được hai giá trị của x đối nhau.
Do đó để phương trình có hai nghiệm phân biệt thuộc đoạn \left[ { - \sqrt 2 ;\sqrt 3 } \right] thì phương trình phải có hai nghiệm phân biệt đối nhau thuộc \left[ { - \sqrt 2 ;\sqrt 2 } \right] và x \ne 0.
Dễ thấy x \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\backslash \left\{ 0 \right\} \Rightarrow {x^2} \in \left( {0;2} \right] \Rightarrow 4 - {x^2} \in \left[ {2;4} \right)
\Rightarrow \sqrt {4 - {x^2}} \in \left[ {\sqrt 2 ;2} \right) \Rightarrow 3 - \sqrt {4 - {x^2}} \in \left( {1;3 - \sqrt 2 } \right]
\Rightarrow t \in \left( {1;3 - \sqrt 2 } \right] \Rightarrow f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right] vì f\left( t \right) đồng biến trên \left( {1;3 - \sqrt 2 } \right].
Phương trình đã cho có hai nghiệm {x_1},{x_2} phân biệt thuộc đoạn \left[ { - \sqrt 2 ;\sqrt 3 } \right] thì phương trình f\left( t \right) = m có nghiệm duy nhất t \in \left( {1;3 - \sqrt 2 } \right]
\Rightarrow m = f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right] = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right].
Vậy S = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right].
Cho hàm số y = f\left( x \right) có bảng biến thiên như sau:
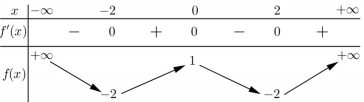
Số nghiệm thực của phương trình 2f\left( x \right) + 3 = 0 là:
Ta có: Pt \Leftrightarrow 2f\left( x \right) = - 3 \Leftrightarrow f\left( x \right) = - \dfrac{3}{2}.\;\;\left( * \right)
Số nghiệm của phương trình \left( * \right) là số giao điểm của đồ thị hàm số y = f\left( x \right) và đường thẳng y = - \dfrac{3}{2}.
Dựa vào BBT ta thấy đường thẳng y = - \dfrac{3}{2} cắt đồ thị hàm số y = f\left( x \right) tại 4 điểm phân biệt.
\Rightarrow Pt\;\;\left( * \right) có 4 nghiệm phân biệt.

