Đề thi THPT QG – 2021 lần 1– mã 104
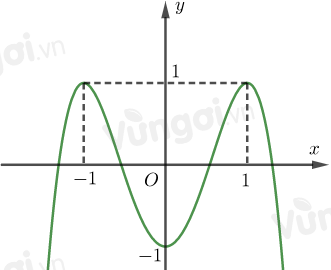
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong trong hình trên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là
Ta có: \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\,\,\,\left( {a < - 1} \right)\\f\left( x \right) = b\,\,\,\left( { - 1 < b < 0} \right)\\f\left( x \right) = c\,\,\,\left( {0 < c < 1} \right)\\f\left( x \right) = d\,\,\,\left( {d > 1} \right)\end{array} \right.\)
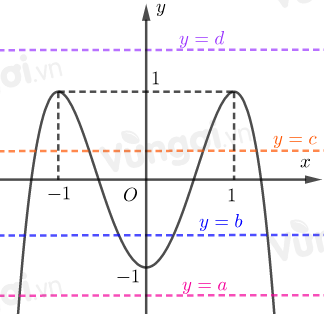
Dựa vào đồ thị ta thấy:
\(f\left( x \right) = a\) với \(a < - 1\) có \(2\) nghiệm.
\(f\left( x \right) = b\,\,\left( { - 1 < b < 0} \right)\) có \(4\) nghiệm.
\(f\left( x \right) = c\) với \(0 < c < 1\) có \(4\) nghiệm.
\(f\left( x \right) = d\) với \(d > 1\) vô nghiệm.
Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là \(10.\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
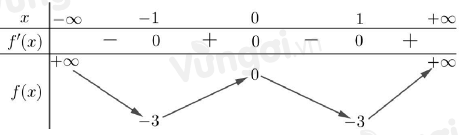
Phương trình \(f\left( {{x^2} - 1} \right) + 2 = 0\) có bao nhiêu nghiệm thực?
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
Đặt \(t = {x^2} - 1\,\,\left( {t \ge - 1} \right)\).
Phương trình đã cho trở thành: \(f\left( t \right) + 2 = 0\).
\( \Leftrightarrow f\left( t \right) = - 2\), với \(t \ge - 1\) (*).
Dựa vào bảng biến thiên, ta thấy đường thẳng \(y = - 2\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại 4 điểm phân biệt. Trong đó, có 3 điểm phân biệt có hoành độ lớn hơn hoặc bằng \( - 1\).
Suy ra phương trình (*) có 3 nghiệm thực \(t\).
Khi đó ứng với mỗi nghiệm thực \(t\) thì có 2 nghiệm thực \(x\).
Vậy phương trình đã cho có tổng cộng 6 nghiệm thực phân biệt.
Đồ thị hàm số \(y = {x^3} - 3{x^2} + 5x - 4\) đi qua điểm nào dưới đây?
Thay tọa độ điểm Q vào hàm số ta có: \( - 4 = {0^3} - {3.0^2} + 5.0 - 4\) (đúng).
Vậy điểm \(Q\left( {0; - 4} \right)\) thuộc đồ thị hàm số \(y = {x^3} - 3{x^2} + 5x - 4\).
Cho hàm số \(y=f\left( x \right)\) xác định trên R và có bảng biến thiên như sau :
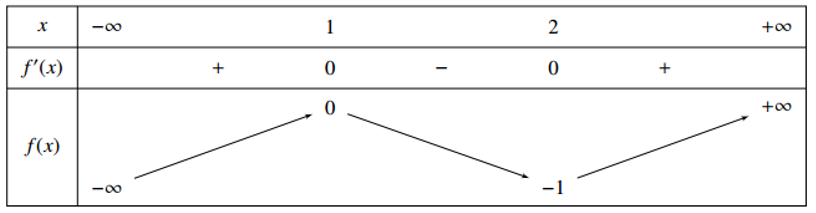
Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y=|f\left( |x| \right)+m|\) có 11 điểm cực trị
Xét đồ thị \(y=|f\left( |x| \right)+m|\) khi m thay đổi thì đồ thị hàm số sẽ tịnh tiến dọc theo trục Oy.
Từ bảng biến thiên ta thấy \(y=f\left( x \right)\) đồ thị hàm số đã có 2 điểm cực trị nằm bên phải trục Oy.
Vậy nếu giả sử \(y=f\left( x \right)+m\) cắt Ox tại 3 điểm có hoành độ dương thì đồ thị hàm số \(y=|f\left( x \right)+m|\) sẽ có 5 điểm cực trị ( theo lí thuyết phần phương pháp ).
Suy ra đồ thị hàm số \(y=|f\left( |x| \right)+m|\) sẽ có 11 điểm cực trị (theo lí thuyết phần phương pháp).
Như vậy ta tìm điều kiện của m để phương trình \(f\left( x \right)+m=0\) có 3 nghiệm dương phân biệt.
Từ bảng biến thiên dễ thấy với \(0 < m < 1\) thỏa mãn.
Cho hàm số \(f\left( x \right)={{x}^{3}}-3{{x}^{2}}.\) Có bao nhiêu giá trị nguyên của \(m\) để đồ thị hàm số \(g\left( x \right)=f\left( \left| x \right| \right)+m\) cắt trục hoành tại 4 điểm phân biệt ?
Dựa vào đồ thị hàm số \(f\left( \left| x \right| \right)={{\left| x \right|}^{3}}-3{{\left| x \right|}^{2}},\) hình vẽ bên dưới:
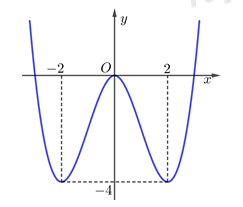
Để phương trình \(g\left( x \right)=0\Leftrightarrow f\left| \left( x \right) \right|=-\,m\) có 4 nghiệm phân biệt \(\Leftrightarrow \)\(-\,4<-\,m<0\Leftrightarrow 0<m<4.\)
Kết hợp với điều kiện \(m\in \mathbb{Z}\)\(\xrightarrow{{}}\,\,m=\left\{ 1;\,\,2;\,\,3 \right\}\) là các giá trị cần tìm.
Cho hàm số \(y={{x}^{3}}-3x+2\) có đồ thị như hình vẽ. Giá trị của m để phương trình \(\left| {{x}^{3}}-3x+2 \right|={{2}^{m}}\) có 3 nghiệm thực là
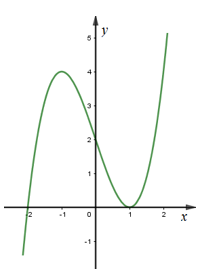
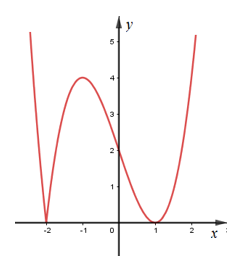
Vẽ đồ thị hàm số \(y=\left| {{x}^{3}}-3x+2 \right|\) dựa vào đồ thị hàm số \(y={{x}^{3}}-3x+2\).
Đánh giá vị trí của đường thẳng \(y={{2}^{m}}\) để đồ thị hàm số cắt đường thẳng \(y={{2}^{m}}\) tại 3 điểm phân biệt.
Kết luận giá trị của m.
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
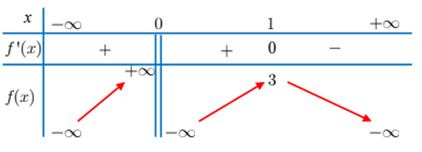
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?
Quan sát đồ thị hàm số ta thấy:
+) Với \(m < 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm phân biệt.
+) Với \(m = 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(2\) điểm phân biệt.
+) Với \(m > 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất \(1\) điểm.
Vậy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại nhiều nhất \(3\) điểm.
Do đó phương trình đã cho có nhiều nhất \(3\) nghiệm.
Tìm tập hợp tất cả các giá trị thực của m để đồ thị \(\left( {{C}_{m}} \right)\) của hàm số \(y={{x}^{4}}-m{{x}^{2}}+2m-3\) có 4 giao điểm với đường thẳng \(y=1\), có hoành độ nhỏ hơn 3.
Xét phương trình hoành độ giao điểm \({{x}^{4}}-m{{x}^{2}}+2m-3=1\) \(\Leftrightarrow {{x}^{4}}-m{{x}^{2}}+2m-4=0\,\,\left( * \right)\)
Để để đồ thị \(\left( {{C}_{m}} \right)\) của hàm số \(y={{x}^{4}}-m{{x}^{2}}+2m-3\) có 4 giao điểm với đường thẳng \(y=1\), có hoành độ nhỏ hơn 3 \(\Rightarrow \) Phương trình (*) có 4 nghiệm phân biệt nhỏ hơn 3.
Đặt \({{x}^{2}}=t\,\,\left( 0\le t<9 \right)\), khi đó \(\left( * \right)\Leftrightarrow {{t}^{2}}-mt+2m-4=0\,\,\,\left( ** \right)\) , phương trình này có 2 nghiệm phân biệt thuộc \(\left( 0;9 \right)\).
\(\left( {**} \right) \Leftrightarrow \left( {{t^2} - 4} \right) - m\left( {t - 2} \right)=0 \) \(\Leftrightarrow \left[ \begin{array}{l}t - 2 = 0\\t + 2 - m = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}t = 2\left( {tm} \right)\\t = m - 2\end{array} \right.\)
Để phương trình có 2 nghiệm phân biệt thuộc \(\left( {0;9} \right) \) \(\Rightarrow \left\{ \begin{array}{l}0 < m - 2 < 9\\m - 2 \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 < m < 11\\m \ne 4\end{array} \right.\)
Cho hàm số \(y={{x}^{3}}-2\left( m+1 \right){{x}^{2}}+\left( 5m+1 \right)x-2m-2\) có đồ thị là \(\left( {{C}_{m}} \right)\), với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn \(\left[ -10;100 \right]\) để \(\left( {{C}_{m}} \right)\) cắt trục hoành tại ba điểm phân biệt \(A\left( 2;0 \right),B,C\) sao cho trong hai điểm \(B,C\) có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình \({{x}^{2}}+{{y}^{2}}=1\) ?
Đồ thị hàm số \(y={{x}^{3}}-2\left( m+1 \right){{x}^{2}}+\left( 5m+1 \right)x-2m-2\) luôn đi qua điểm \(A\left( 2;0 \right)\)
Xét phương trình hoành độ giao điểm
\(\begin{array}{l}
\,\,\,\,{x^3} - 2\left( {m + 1} \right){x^2} + \left( {5m + 1} \right)x - 2m - 2 = 0\\
\Leftrightarrow \left( {x - 2} \right)\left( {{x^2} - 2mx + m + 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
{x^2} - 2mx + m + 1 = 0\,\,\left( * \right)
\end{array} \right.
\end{array}\)
Để phương trinh có 3 nghiệm phân biệt \(\Leftrightarrow pt\,\left( * \right)\) có 2 nghiệm phân biệt khác 2
\( \Leftrightarrow \left\{ \begin{array}{l}
\Delta ' = {m^2} - m - 1 > 0\\
{2^2} - 2m.2 + m + 1 \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m \in \left( { - \infty ;\dfrac{{1 - \sqrt 5 }}{2}} \right) \cup \left( {\dfrac{{1 + \sqrt 5 }}{2}; + \infty } \right)\\
m \ne \dfrac{5}{3}
\end{array} \right.\)
Giả sử \({{x}_{B}};{{x}_{C}}\,\,\left( {{x}_{B}}<{{x}_{C}} \right)\) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn \({{x}^{2}}+{{y}^{2}}=1\)
TH1: \({x_B} < - 1 < {x_C} < 1 \Rightarrow \left\{ \begin{array}{l}
af\left( { - 1} \right) < 0\\
af\left( 1 \right) > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3m + 2 < 0\\
- m + 2 > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m < \dfrac{{ - 2}}{3}\\
m < 2
\end{array} \right. \) \(\Leftrightarrow m < \dfrac{{ - 2}}{3}\)
TH2: \( - 1 < {x_B} < 1 < {x_C} \Leftrightarrow \left\{ \begin{array}{l}
af\left( { - 1} \right) > 0\\
af\left( 1 \right) < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3m + 2 > 0\\
- m + 2 < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m > - \dfrac{2}{3}\\
m > 2
\end{array} \right.\) \( \Leftrightarrow m > 2\)
Kết hợp điều kiện ta có: \(m\in \left( -\infty ;-\dfrac{2}{3} \right)\cup \left( 2;+\infty \right)\).
Lại có \(m\in \left[ -10;100 \right]\) \(\Rightarrow m\in \left[ -10;-\dfrac{2}{3} \right)\cup \left( 2;100 \right]\)
\(\Rightarrow \) có \(108\) giá trị m nguyên thỏa mãn yêu cầu bái toán.
Số giao điểm của đồ thị \(y={{x}^{3}}-4x+3\) với đồ thị hàm số \(y=x+3\) là
Phương trình hoành độ giao điểm của hai đồ thị là \({{x}^{3}}-4x+3=x+3\Leftrightarrow x\left( {{x}^{2}}-5 \right)=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\pm \,\sqrt{5} \\ \end{align} \right..\)
Vậy hai đồ thị cắt nhau tại 3 điểm phân biệt.
Tìm $m$ để đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ cắt đường thẳng $y = m\left( {x - 1} \right)$ tại ba điểm phân biệt có hoành độ ${x_1},{x_2},{x_3}$ thỏa mãn $x_1^2 + x_2^2 + x_3^2 = 5$.
Phương trình hoành độ giao điểm:
${x^3} - 3{x^2} + 2 = m\left( {x - 1} \right) \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - 2 - m} \right) = 0 $
$\Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ {x^2} - 2x - 2 - m = 0\left( * \right) \hfill \\ \end{gathered} \right.$
Để hai đồ thị hàm số cắt nhau tại ba điểm phân biệt thì phương trình hoành độ có 3 nghiệm phân biệt
$ \Leftrightarrow \left( * \right)$ có 2 nghiệm phân biệt khác $1 \Leftrightarrow \left\{ \begin{gathered} \Delta ' = 1 + 2 + m > 0 \hfill \\ 1 - 2 - 2 - m \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow m > - 3$
Gọi ${x_1} = 1,{x_2},{x_3}$ lần lượt là nghiệm của phương trình $\left( * \right) \Rightarrow {x_2} + {x_3} = 2;{x_2}{x_3} = - 2 - m$
Ta có: $x_1^2 + x_2^2 + x_3^2 = 5 \Leftrightarrow {\left( {{x_2} + {x_3}} \right)^2} - 2{x_2}{x_3} = 4 $
$\Leftrightarrow 4 - 2\left( { - 2 - m} \right) = 4 \Leftrightarrow m = - 2$
Đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2x-1\) cắt đồ thị hàm số \(y={{x}^{2}}-3x+1\) tại hai điểm phân biệt \(A,\,\,B.\) Tính độ dài \(AB.\)
Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(\left( P \right)\) là \({{x}^{3}}-3{{x}^{2}}+2x-1={{x}^{2}}-3x+1\)
\(\Leftrightarrow {{x}^{3}}-4{{x}^{2}}+5x-2=0\Leftrightarrow \left( x-2 \right){{\left( x-1 \right)}^{2}}=0\Leftrightarrow \left[ \begin{align} & x=1\,\,\Rightarrow \,\,y\left( 1 \right)=-\,1 \\& x=2\,\,\Rightarrow \,\,y\left( 2 \right)=-\,1 \\ \end{align} \right..\)
Khi đó \(A\left( 1;-\,1 \right),\,\,B\left( 2;-\,1 \right)\) \(\xrightarrow{{}}\,\,\overrightarrow{AB}=\left( 1;0 \right)\Rightarrow AB=1.\)
Đồ thị hàm số \(y = {x^4} - {x^2} + 1\) và đồ thị của hàm số \(y = - {x^2}\) có tất cả bao nhiêu điểm chung?
Xét phương trình hoành độ giao điểm \({x^4} - {x^2} + 1 = - {x^2} \Leftrightarrow {x^4} + 1 = 0 \)
\(\Rightarrow \) Phương trình vô nghiệm.
Vậy hai đồ thị hàm số không có điểm chung.
Đề thi THPT QG - 2021 - mã 102
Đồ thị của hàm số \(y = - {x^4} - 2{x^2} + 3\) cắt trục tung tại điểm có tung độ bằng
Đồ thị hàm số \(y = - {x^4} - 2{x^2} + 3\) cắt trục tung tại điểm có tung độ: \(y = 3\)
Số giao điểm của đồ thị hàm số $y = 2{x^3}-3{x^2}$ và đường thẳng $y = - 5$ là:
Phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng là:
$\begin{array}{l}2{x^3}-3{x^2}\; = - 5\\ \Leftrightarrow 2{x^3}-3{x^2}\; + 5 = 0\\ \Leftrightarrow x = - 1\end{array}$
Đề thi THPT QG - 2021 - mã 101
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 1\) là
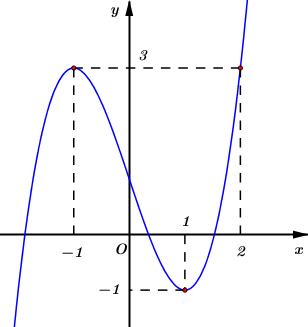
+ Để giải phương trình \(f\left( {f\left( x \right)} \right) = 1\) ta đi xét phương trình \(f\left( x \right) = 1\).
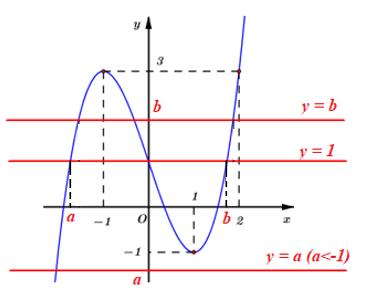
Từ đồ thị \(f\left( x \right)\) kẻ tương giao với đường thẳng \(y = 1 \Rightarrow \) Phương trình \(f\left( x \right) = 1 \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\,voi\,\,a < - 1\\x = 0\\x = b\,\,voi\,\,b \in \left( {1;2} \right)\end{array} \right.\).
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 1\)\( \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a \to ke\,\,tuong\,\,giao\,\,\left( {a < - 1} \right) \Rightarrow 1\,\,nghiem\\f\left( x \right) = 0 \to ke\,\,tuong\,\,giao \Rightarrow 3\,\,nghiem\\f\left( x \right) = b \to ke\,\,tuong\,\,giao\,\,b \in \left( {1;2} \right) \Rightarrow 3\,\,nghiem\end{array} \right.\)
\( \Rightarrow \) Phương trình \(f\left( {f\left( x \right)} \right) = 1\) có 7 nghiệm phân biệt.
Tìm số giao điểm của đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ và $y = - {x^2} + 7x - 11$
Xét phương trình
$\begin{array}{l}{x^3} - 3{x^2} + 2 = - {x^2} + 7x - 11\\ \Leftrightarrow {x^3} - 3{x^2} + 2 - \left( { - {x^2} + 7x - 11} \right) = 0\\ \Leftrightarrow {x^3} - 2{x^2} - 7x + 13 = 0\end{array}$
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} - 7x + 13\) trên tập số thực \(\mathbb{R}\) có:
\(f'\left( x \right) = 3{x^2} - 4x - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \dfrac{7}{3}\end{array} \right.\)
Bảng biến thiên
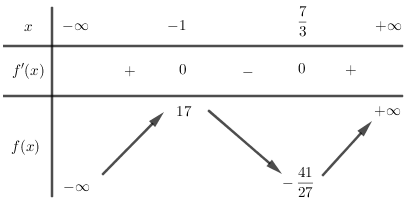
Quan sát bảng biến thiên ta thấy hàm số có \({y_{CD}}.{y_{CT}} < 0\) nên phương trình \(y = 0\) có \(3\) nghiệm phân biệt.
Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = - {x^3} + 2{x^2} - m$ cắt trục hoành tại đúng một điểm
Yêu cầu bài toán \( \Leftrightarrow \) phương trình $ - {x^3} + 2{x^2}-m\; = 0$ có đúng một nghiệm thực
\( \Leftrightarrow \) đường thẳng $y = m$ có đúng $1$ điểm chung với đồ thị hàm số: $y = f(x) = - {x^3} + 2{x^2}$
Lập bảng biến thiên của hàm số: $y = f(x) = - {x^3} + 2{x^2}$
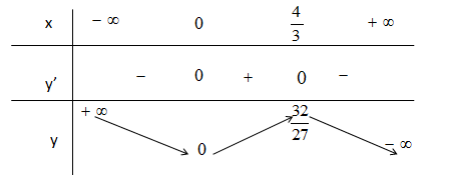
Dựa vào bảng biến thiên ta được kết quả: $m < 0$ hoặc $m > \dfrac{{32}}{{27}}$
Tìm tất cả các giá trị thực của tham số $m$ để đường thẳng $d:y = - \,mx$ cắt đồ thị của hàm số $y = {x^3} - 3{x^2} - m + 2$ $\left( C \right)$ tại ba điểm phân biệt $A,{\rm{ }}B,{\rm{ }}C$ sao cho $AB = BC$.
Phương trình hoành độ giao điểm: ${x^3} - 3{x^2} - m + 2 = - \,mx$
$ \Leftrightarrow {x^3} - 3{x^2} + 2 + m\left( {x - 1} \right) = 0 \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x + m - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x + m - 2 = 0\,\,\,\,\,\left( * \right)\end{array} \right..$
Để $d$ cắt $\left( C \right)$ tại ba điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt khác \(1\)
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{1^2} - 2.1 + m - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 - \left( {m - 2} \right) > 0\\m \ne 3\end{array} \right. \Leftrightarrow m < 3.$
Do \(B\) là trung điểm của \(AC\) nên \(A,B,C\) cùng thuộc đồ thị hàm số \(\left( C \right)\) và \(A,C\) đối xứng nhau qua \(B\)
Điều này có nghĩa là \(B\) chính là điểm uốn của \(\left( C \right)\). Bài toán trở thành tìm \(m\) để \(d\) đi qua điểm uốn của \(\left( C \right)\).
Ta xét $y = {x^3} - 3{x^2} - m + 2$ có \(y' = 3{x^2} - 6x;y'' = 6x - 6 = 0 \Leftrightarrow x = 1\) suy ra \(B\left( {1; - m} \right)\)
Dễ thấy \(B \in d\) hay \(d\) luôn đi qua \(B\) với mọi \(m\).
Kết hợp điều kiện để phương trình có ba nghiệm phân biệt ta được \(m < 3\).
Vậy với \(m < 3\) thỏa mãn yêu cầu bài toán.
Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị $\left( C \right).$ Gọi $d$ là đường thẳng đi qua $A\left( {3;20} \right)$ và có hệ số góc $m.$ Giá trị của $m$ để đường thẳng $d$ cắt $\left( C \right)$ tại $3$ điểm phân biệt
Gọi \(d:y = mx + n\).
\(d\) đi qua \(A\left( {3;20} \right)\) nên \(20 = 3m + n \Leftrightarrow n = 20 - 3m\) hay \(d:y = mx + 20 - 3m\)
Xét phương trình hoành độ giao điểm của \(d\) và \(\left( C \right)\):
\({x^3} - 3x + 2 = mx + 20 - 3m\)\( \Leftrightarrow {x^3} - \left( {m + 3} \right)x + 3m - 18 = 0\) \( \Leftrightarrow m(x - 3) = {x^3} - 3x - 18\) \( \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} + 3x + 6 - m} \right) = 0\)
Để $d$ cắt đồ thị tại $3$ điểm phân biệt thì phương trình có \(3\) nghiệm phân biệt
Suy ra phương trình ${x^2} + 3x + 6 - m = 0$ có $2$ nghiệm phân biệt khác \(3\)
Điều kiện:
$\left\{ \begin{array}{l}
\Delta = {3^2} - 4\left( {6 - m} \right) > 0\\
{3^2} + 3.3 + 6 - m \ne 0
\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}
- 15 + 4m > 0\\
24 - m \ne 0
\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}
m > \dfrac{{15}}{4}\\
m \ne 24
\end{array} \right.$

