Câu hỏi:
2 năm trước
Tìm số giao điểm của đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ và $y = - {x^2} + 7x - 11$
Trả lời bởi giáo viên
Đáp án đúng: d
Xét phương trình
$\begin{array}{l}{x^3} - 3{x^2} + 2 = - {x^2} + 7x - 11\\ \Leftrightarrow {x^3} - 3{x^2} + 2 - \left( { - {x^2} + 7x - 11} \right) = 0\\ \Leftrightarrow {x^3} - 2{x^2} - 7x + 13 = 0\end{array}$
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} - 7x + 13\) trên tập số thực \(\mathbb{R}\) có:
\(f'\left( x \right) = 3{x^2} - 4x - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \dfrac{7}{3}\end{array} \right.\)
Bảng biến thiên
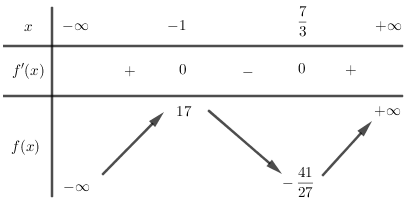
Quan sát bảng biến thiên ta thấy hàm số có \({y_{CD}}.{y_{CT}} < 0\) nên phương trình \(y = 0\) có \(3\) nghiệm phân biệt.
Hướng dẫn giải:
Số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đồ thị hàm số $y = g\left( x \right)$ bằng số nghiệm của phương trình $f\left( x \right) = g\left( x \right)$
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
