Tính thể tích khối lăng trụ ABCD⋅A′B′C′D′
Bước 1: Gọi M là trung điểm AB,I là trung điểm AM. Tính góc A’IH
Ta có SABCD=2SABC=a2√32
Gọi M là trung điểm AB,I là trung điểm AM
Khi đó HI⊥AB⇒ góc giữa (ABB′A′) và (ABCD) là góc ^A′IH=60∘
Bước 2: Tính VABCD⋅A′B′C′D′
Ta có IH=12CM=a√34⇒A′H=IH⋅tan60∘=3a4
⇒VABCD⋅A′B′C′D′=A′H⋅SABCD=3a4⋅a2√32=3a3√38.
Tính góc giữa hai mặt phẳng (ABB′A′) và (ABC)
Bước 1: Tính diện tích tam giác ABH
Hình thoi ABCD có ^BCD=120∘
⇒^ABC=60∘
Do đó ABC là tam giác đều
⇒SABC=a2√34
⇒SABH=12SABC=a2√38.
Bước 2: Sử dụng công thức liên hệ giữa diện tích hình chiếu của đa giác và đa giác ban đầu.
Tam giác ABH là hình chiếu của tam giác A′BH
Gọi góc giữa (ABB′A′) và (ABCD) là φ
Khi đó ta có SABH=SABA′cosφ⇒cosφ=SABHSABA′=12⇒φ=60∘
Cho khối lăng trụ có diện tích đáy B và chiều cao h. Thể tích V của khối lăng trụ đã cho được tính theo công thức nào dưới đây?
Thể tích V của khối lăng trụ có diện tích đáy B và chiều cao h là: V=Bh
Đề thi THPT QG 2019 – mã đề 104
Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là
Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là Bh..
Đề thi THPT QG - 2021 - mã 103
Thể tích của khối lập phương cạnh 3a bằng:
Vlapphuong=(canh)3=(3a)3=27a3.
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AA' và BB'. Đường thẳng CM cắt đường thẳng C’A' tại P, đường thẳng CN cắt đường thẳng C’B' tại Q. Thể tích của khối đa diện lồi A’MPB’NQ bằng:
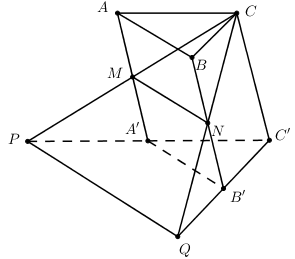
Gọi diện tích đáy, chiều cao, thể tích của hình lăng trụ ABC.A’B’C’ lần lượt là S;h;V⇒V=Sh.
Ta có: ΔA′B′C′∼ΔPQC′ theo tỉ số 12⇒SC′PQ=4SA′B′C′=4S.
⇒VC.C′PQ=13.h.4S=43V.
Ta có : SABNM=12SABB′A′⇒VC.ABNM=12VC.ABB′A′
Mà VC.ABB′A′=23V⇒VC.ABNM=12.23V=V3⇒VCC′A′B′NM=V−V3=23V
Vậy VA′MPB′NQ=43V−23V=23V.
Cho hình lăng trụ đứng ABCD⋅A′B′C′D′ với đáy là hình thoi có cạnh bằng 4a,AA′=6a,^BCD=1200. Goi M,N,K lần lượt là trung điểm của AB′,B′C,BD′. Tính thể tích khối đa diện lồi có các đỉnh là các điểm A,B,C,M,N,K.

Gọi V là thể tích của khối lăng trụ ABCD⋅A′B′C′D′.
Gọi A1,B1,C1 lần lượt là giao điểm của AA′,BB′,CC′ và mặt phẳng (MNK).
Thể tích của khối lăng trụ ABC⋅A1B1C1 là:
VABC⋅A1B1C1=14VABCD⋅A′B′C′D′=14V.
Gọi V1,V2,V3 lần lượt là thể tích của khối tứ diện A.A1MK,B.B1MN,C.C1NK.
Ta có:
+) V1=VA⋅A1MK=13⋅SΔA1MK⋅AA1
=13⋅14SΔA1B1C1⋅AA1=112⋅VABC⋅A1B1C1=112⋅14V=148V
+)V2=VB⋅B1MN=13⋅SΔB1MN⋅BB1=13⋅14SΔB1A1C1⋅BB1=112⋅VABC⋅A1B1C1=112⋅14V=148V
V3=VC.C1NK=13⋅SΔC1NK⋅CC1=13⋅14SΔC1B1A1⋅CC1=112⋅VABC⋅A1B1C1=112⋅14V=148V
V=SABCD⋅A′A=2SΔBCD⋅A′A=2⋅12⋅(4a)⋅(4a)⋅sin1200⋅(6a)=48a3√3
Do đó, thể tích khối đa diện lồi ABCMNK là:
VABCMNK=14VABCD⋅A′B′C′D′−(V1+V2+V3)=14V−3⋅148V=316V=316⋅48a3√3=9a3√3.
Vậy VABCMNK=9a3√3
Đề thi THPT QG 2019 – mã đề 104
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác đều cạnh a và AA′=√2a (minh họa như hình vẽ bên).
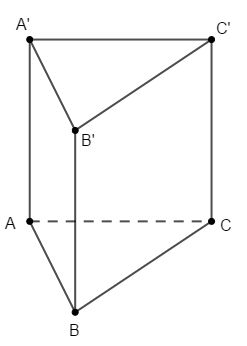
Thể tích của khối lăng trụ đã cho bằng
Tam giác ABC đều cạnh a⇒SΔABC=a2√34.
Vậy VABC.A′B′C′=AA′.SΔABC=√2a.a2√34=a3√64.
Cho hình hộp ABCD.A′B′C′D′. Gọi V1;V2 lần lượt là thể tích của khối tứ diện ACB′D′ và khối hộp ABCD.A′B′C′D′. Tỉ số V1V2 bằng
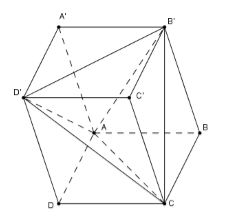
Ta thấy V1=VABCD.A′B′C′D′=h.SABCD với h=d(A′,(ABCD))
+) VD′.ADC=13d(D′,(ADC)).SΔADC=13.h.12SABCD=16V1
Tương tự ta có VC.D′C′B′=VB′.ABC=VA.A′B′D′=VD′.ADC=16V1
Lại có VC.D′C′B′+VB′.ABC+VA.A′B′D′+VD′.ADC+VACB′D′=VABCD.A′B′C′D′
⇔V2=VACB′D′=V1−4.16V1=V13⇔V1V2=13.
Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, BD=2a, góc giữa hai mặt phẳng (A′BD) và (ABCD) bằng 600. Thể tích của khối hộp chữ nhật đã cho bằng:
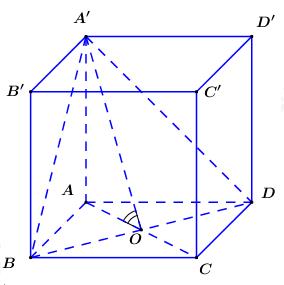
* Xác định ∠((A′BD);(ABCD)).
+ (A′BC)∩(ABCD)=BD.
+ {AA′⊥BDAO⊥BD⇒(A′AO)⊥BD.
+ {(A′AO)∩(A′BD)=A′O(A′AO)∩(ABCD)=AO
⇒∠((A′BD);(ABCD))=∠(A′O;AO)=∠A′OA.
⇒∠A′OA=600.
* Xét tam giác A′OA vuông tại A có AO=12AC=12BD=a.
⇒AA′=tan600.AO=a√3.
⇒VABCD.A′B′C′D′=SABCD.AA′=12AC.BD.AA′ =12.(2a)2.a√3=2√3a3.
Thể tích của khối hộp chữ nhật có ba kích thước lần lượt là 1,2,3 bằng:
Hình hộp chữ nhật có 3 kích thước lần lượt 1,2,3 là V=1.2.3=6.
Cho khối lăng trụ ABC.A′B′C′. Gọi E,F lần lượt là trung điểm của AA′,CC′. Mặt phẳng (BEF) chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là:
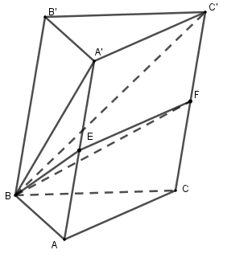
Ta có: VABC.A′B′C′=d(B;(A′B′C′)).SA′B′C′=V
VB.A′B′C′=13d(B;(A′B′C′)).SA′B′C′=13V
Suy ra VB.AA′C′C=VABC.A′B′C′−VB.A′B′C′ =V−13V=23V
Lại có: SACFE=12SAA′C′C (do E, F lần lượt là trung điểm của AA’, CC’)
Suy ra VB.AEFC=13d(B,(AA′C′C)).SACFE =13d(B,(AA′C′C)).12SAA′C′C
=12.13d(B,(AA′C′C)).SAA′C′C =12VB.AA′C′C=12.23V=13V
Suy ra VBEFA′B′C′=VABC.A′B′C′−VB.ACFE =V−13V=23V
Vậy tỉ số thể tích giữa hai phần là: VB.ACFE:VBEFA′B′C′=13V:23V=1:2
Đề thi THPT QG 2019 – mã đề 104
Cho lăng trụ ABC.A′B′C′ có chiều cao bằng 4 và đáy là tam giác đều cạnh bằng 4. Gọi M,N và P lần lượt là tâm của các mặt bên ABB′A′,ACC′A′ và BCC′B′. Thể tích của khối đa diện lồi có các đỉnh là các điểm A,B,C,M,N,P bằng
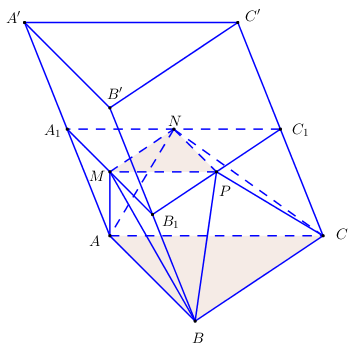
Gọi V là thể tích khối lăng trụ ABC.A′B′C′.
Gọi A1,B1,C1 lần lượt là trung điểm của AA′,BB′,CC′. Khi đó ta có (A1B1C1)//(ABC)//(A′B′C′)
Khi đó VABC.MNP=VABC.A1B1C1−VA.A1MN−VB.B1MP−VC.C1NP.
Ta có VABC.A1B1C1=12VABC.A′B′C′=12V.
VA.A1MN=13d(A;(A1B1C1)).SA1MN=13.12d((ABC);(A′B′C′)).14SABC=124V.
Chứng minh tương tự ta có VB.B1MP=VC.C1NP=V24.
⇒VABCMNP=12V−3.V24=3V8.
Ta có V=4.42√34=16√3⇒VABCMNP=3.16√38=6√3.
Cho khối lăng trụ có chiều cao h=5 và diện tích đáy S=6. Thể tích của khối lăng trụ đã cho là:
Thể tích của khối lăng trụ đã cho là: V=Sh=6.5=30.
Cho khối lăng trụ đều ABC.A′B′C′ có AB=2a,M là trung điểm của BC và A′M=3a. Thể tích khối lăng trụ đã cho bằng:
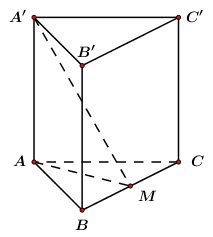
Ta có: SABC=(2a)2.√34=a2√3.
Ta có: AM là đường trung tuyến của ΔABC đều cạnh 2a ⇒AM=2a√32=a√3.
Áp dụng định lý Pitago cho ΔAA′M vuông tại A ta có: AA′=√A′M2−AM2 =√9a2−3a2=a√6
⇒VABC.A′B′C′=AA′.SABC =a√6.a2√3=3a3√2
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân tại C,A′C=a√5,BC=a,∠ACB=450. Thể tích khối lăng trụ ABC.A′B′C′ bằng:
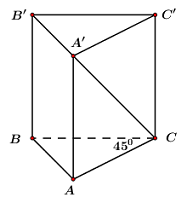
Ta có: ΔABC cân tại C ⇒AC=BC=a.
⇒SABC=12AC.BC.sinC =12.a.a.sin450=12a2.√22=a2√24.
Áp dụng định lý Pitago cho ΔAA′C vuông tại A ta có:
AA′=√A′C2−AC2 =√5a2−a2=2a
⇒VABC.A′B′C′=AA′.SABC =2a.a2√24=a3√22.
Nếu một khối lăng trụ đứng có diện tích đát bằng B và cạnh bên bằng h thì có thể tích là:
Thể tích khối lăng trụ đã cho là: V=Bh.
Thể tích của khối hộp chữ nhật có ba kích thước là 3; 4; 5 bằng:
Thể tích của khối hộp chữ nhật đã cho là:V=abc=3.4.5=60.
Khối lăng trụ đáy là hình chữ nhật có hai kích thước lần lượt là 2a,3a, chiều cao khối lăng trụ là 5a. Thể tích khối lăng trụ bằng:
Diện tích đáy của khối lăng trụ đã cho là: S=2a.3a=6a2.
⇒ Thể tích khối lăng trụ đã cho là: V=Sh=6a2.5a=30a3.
Cho khối hộp chữ nhật ABCD.A′B′C′D′ có AB=2,AD=3,AA′=4. Thể tích của khối hộp đã cho bằng:
Thể tích của khối hộp chữ nhật ABCD.A′B′C′D′ đã cho là: V=AB.AD.AA′=2.3.4=24.

