Cho khối lăng trụ có diện tích đáy \(B = 6\) và chiều cao \(h = 2.\) Thể tích của khối lăng trụ đã cho bằng:
Thể tích của khối lăng trụ đã cho là: \(V = Bh = 6.2 = 12.\)
Đề thi THPT QG - 2021 - mã 101
Thể tích của khối lập phương cạnh \(5a\) bằng
\({V_{lap\,\,phuong}} = {\left( {canh} \right)^3} = {\left( {5a} \right)^3} = 125{a^3}\).
Đề thi THPT QG - 2021 - mã 102
Thể tích của khối lập phương cạnh \(4a\) bằng
Thể tích của khối lập phương cạnh \(4a\) là \(V = {\left( {4a} \right)^3} = 64{a^3}\)
Cho khối lăng trụ tứ giác đều có cạnh đáy bằng a, chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
Khối lăng trụ tứ giác đều có đáy là hình vuông và cạnh bên vuông góc với đáy nên ta có:
Diện tích đáy \(B = {a^2}\).
Thể tích khối lăng trụ là: \(V = Bh = {a^2}.2a = 2{a^3}\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 6\), cạnh bên bằng \(\sqrt 5 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\).
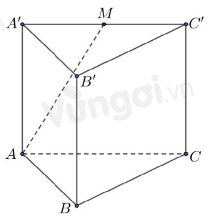
Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng \(\dfrac{{3\sqrt a }}{{47}}\). Tính $a$.
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
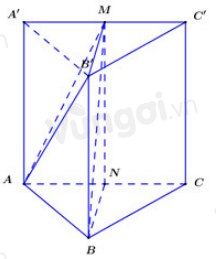
Gọi \(N\) là trung điểm \(AC\).
\( \Rightarrow \left( {BB'M} \right) \equiv \left( {BB'MN} \right)\).
Khi đó \(d\left( {A,\left( {BB'M} \right)} \right) = d\left( {A,\left( {BB'MN} \right)} \right)\).
Vì tam giác \(ABC\) đều nên \(AN \bot BN\).
Ta có \(\left\{ \begin{array}{l}AN \bot BN\\AN \bot MN\\BN,MN \subset \left( {BB'MN} \right)\end{array} \right.\)
\( \Rightarrow AN \bot \left( {BB'MN} \right)\).
\( \Rightarrow d\left( {A,\left( {BB'MN} \right)} \right) = AN = \dfrac{{AC}}{2} = \dfrac{6}{2} = 3\).
Ta lại có \(BN = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \) và \(MN = AA' = \sqrt 5 \).
\( \Rightarrow {S_{BB'MN}} = BN.MN = 3\sqrt 3 .\sqrt 5 = 3\sqrt {15} \)
\( \Rightarrow {S_{BB'M}} = \dfrac{{{S_{BB'MN}}}}{2} = \dfrac{{3\sqrt {15} }}{2}\).
\( \Rightarrow {V_{A.BB'M}} = \dfrac{1}{3}.d\left( {A,\left( {BB'M} \right)} \right).{S_{BB'M}} = \dfrac{1}{3}.3.\dfrac{{3\sqrt {15} }}{2} = \dfrac{{3\sqrt {15} }}{2} = {V_{B'.ABM}}\).
Tam giác \(AA'M\) vuông tại \(A'\): \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {5 + {3^2}} = \sqrt {14} \).
Tam giác \(BB'M\) vuông tại \(B'\): \(BM = \sqrt {B{{B'}^2} + B'{M^2}} = \sqrt {5 + {{\left( {3\sqrt 3 } \right)}^2}} = 4\sqrt 2 \).
Áp dụng công thức Hê–rông, ta có \({S_{ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} = \dfrac{{3\sqrt {47} }}{2}\)
Ta có \({V_{B'.ABM}} = \dfrac{1}{3}.d\left( {B',\left( {ABM} \right)} \right).{S_{ABM}}\)
\( \Rightarrow d\left( {B',\left( {ABM} \right)} \right) = \dfrac{{3.{V_{B'.ABM}}}}{{{S_{ABM}}}} = \dfrac{{3.\dfrac{{3\sqrt {15} }}{2}}}{{\dfrac{{3\sqrt {47} }}{2}}} = \dfrac{{3\sqrt {705} }}{{47}}\).
Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng \(\dfrac{{3\sqrt {705} }}{{47}}\).
Vậy $a=705$.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 4a\), góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^o}\). Thể tích của khối hộp chữ nhật đã cho bằng
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(\left\{ \begin{array}{l}AO \bot BD\\AA' \bot BD\end{array} \right. \Rightarrow A'O \bot BD \Rightarrow\) Góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) là góc giữa A'O và AO và bằng \( \angle AOA' = {60^o}\)
Đáy \(ABCD\) là hình vuông có \(BD = 4a \Rightarrow AB = AD = 2a\sqrt 2 \)
Ta có: \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = 2a.\)
Trong \(\Delta AOA'\) có \(AA' = AO.\tan {60^o} = 2a\sqrt 3 \)
Vậy thể tích khối hộp \(ABCD.A'B'C'D'\) là: \(V = 8{a^2}.2a\sqrt 3 = 16{a^3}\sqrt 3 \)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,\,\,AD = 2a,\,AC' = \sqrt 6 a.\) Thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) bằng:
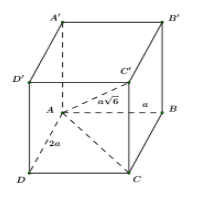
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \) (định lý Pitago)
Xét tam giác \(ACC'\) vuông tại \(C\) ta có:
\(\begin{array}{l}CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {6{a^2} - 5{a^2}} = a.\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = CC'.AB.AD = a.a.2a = 2{a^3}.\end{array}\)
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Cho \(\widehat {BAA'} = {45^0}\). Thể tích của khối lăng trụ đã cho là:
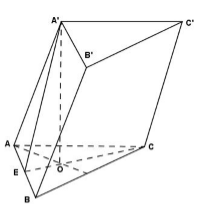
Gọi E là trung điểm của AB ta có:
\(\left\{ \begin{array}{l}OE \bot AB\\A'O \bot AB\left( {A'O \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {A'OE} \right) \Rightarrow AB \bot A'E\)
Tam giác vuông A’EA có \(\widehat {A'AE} = {45^0} \Rightarrow \Delta EAA'\)vuông cân tại E\( \Rightarrow EA' = EA = \dfrac{a}{2};AA' = \dfrac{{a\sqrt 2 }}{2}\)
Tam giác ABC đều cạnh a nên \(CE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OE = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)
\(A'O \bot \left( {ABC} \right) \Rightarrow A'O \bot OE \Rightarrow \Delta A'OE\) vuông tại O
\( \Rightarrow A'O = \sqrt {A'{E^2} - O{E^2}} = \sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{{12}}} = \dfrac{{a\sqrt 6 }}{6}\)
Tam giác ABC đều cạnh a nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'O.{S_{ABC}} = \dfrac{{a\sqrt 6 }}{6}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{8}\)
Trong các mệnh đề sau, mệnh đề nào sau đây sai ?
Thể tích của hình lập phương cạnh a là : $V = {a^3}.$
Diện tích toàn phần của hình lập phương cạnh a là : ${S_{tp}} = 6{a^2}.$
Diện tích toàn phần của hình hộp chữ nhật có các kích thước a, b, h là : ${S_{tp}} = 2h\left( {a + b} \right) + 2ab.$
Thể tích của hình hộp chữ nhật có các kích thước a, b, h là : $V = abh.$
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi cạnh $a\sqrt 3 ,{\mkern 1mu} BD = 3a,$ hình chiếu vuông góc của \(B\) trên mặt phẳng $\left( {A'B'C'D'} \right)$ trùng với trung điểm của \(A’C’\). Gọi $\alpha $ là góc tạo bởi hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {CDD'C'} \right), \cos \alpha = \dfrac{{\sqrt {21} }}{7}$ . Thể tích của khối hộp \(ABCD.A’B’C’D\) bằng
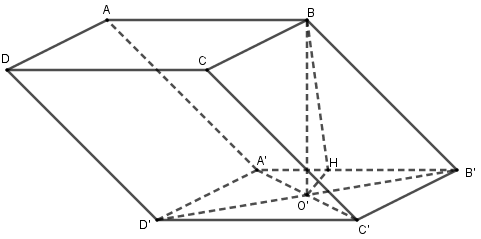
Gọi \(O'\) là trung điểm của \(A'C'\) ta có \(BO' \bot \left( {A'B'C'D'} \right)\)
Dễ thấy \(\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\) và \(\left( {CDD'C'} \right)//\left( {ABB'A'} \right)\) nên góc giữa hai mặt phẳng \(\left( {CDD'C'} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'D'} \right)\).
Xét tam giác \(ABD\) có :
\(\cos \widehat {BAD} = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2.AB.AD}}\)\( = \dfrac{{3{a^2} + 3{a^2} - 9{a^2}}}{{2.a\sqrt 3 .a\sqrt 3 }} = - \dfrac{1}{2}\)
\( \Leftrightarrow \widehat {BAD} = {120^0}\) \( \Rightarrow \widehat {ADC} = {60^0}\)
\( \Rightarrow \Delta ACD\) đều, do đó \( \Rightarrow \Delta A'C'D'\) đều cạnh \(a\sqrt 3 \)
\( \Rightarrow {S_{A'C'D'}} = \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{4}\) \( \Rightarrow {S_{A'B'C'D'}} = 2{S_{A'C'D'}} = \dfrac{{3{a^2}\sqrt 3 }}{2}\)
Kẻ \(O'H \bot A'B'\) thì \(A'B' \bot \left( {BO'H} \right)\) \( \Rightarrow A'B' \bot BH\).
Suy ra góc giữa \(\left( {A'B'C'D'} \right)\) và \(\left( {A'B'BA} \right)\) bằng \(\widehat {\left( {BH,O'H} \right)} = \widehat {BHO'} = \alpha \)
Mà \(\cos \alpha = \dfrac{{\sqrt {21} }}{7}\) nên \(\tan \alpha = \dfrac{2}{{\sqrt 3 }}\) \( \Rightarrow BO' = O'H\tan \alpha = \dfrac{{2O'H}}{{\sqrt 3 }}\)
Lại có \(O'H = A'O'\sin {60^0} = \dfrac{{A'C'}}{2}.\sin {60^0}\) \( = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{4}\) \( \Rightarrow BO' = \dfrac{{2.\dfrac{{3a}}{4}}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{2}\).
Vậy \({V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}.BO'\) \( = \dfrac{{3{a^2}\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{9{a^3}}}{4}\)
Cho hình lăng trụ tam giác \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(a\), cạnh bên tạo với đáy một góc \({60^0}\). Gọi \(M\) là trung điểm của cạnh \(BC\) và \(I\) là trung diểm của \(AM\). Biết rằng hình chiếu của điểm \(I\) lên mặt đáy \(A’B’C’\) là trọng tâm \(G \) của tam giác \(A’B’C’.\) Thể tích khối lăng trụ là:
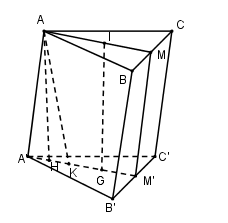
Gọi M’ là trung điểm của B’C’, \(K \in A'M'\) sao cho A’K = KG = GM’
Kẻ \(AH \bot A'M'\left( {H \in A'M'} \right) \Rightarrow AH \bot \left( {A'B'C'} \right) \Rightarrow A'H\)là hình chiếu vuông góc của AA’ trên (A’B’C’)
\( \Rightarrow \widehat {\left( {AA';\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {AA'H} = {60^0}\)
Ta có AHGI là hình chữ nhật nên
\(\begin{array}{l}AI = HG = \dfrac{1}{2}AM = \dfrac{1}{2}A'M';GM' = \dfrac{1}{3}A'M'\\ \Rightarrow A'H = A'M' - HG - GM' = A'M' - \dfrac{1}{2}A'M' - \dfrac{1}{3}A'M' = \dfrac{1}{6}A'M'\end{array}\)
Tam giác ABC đều cạnh a nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
\(A'M' = \dfrac{{a\sqrt 3 }}{2} \Rightarrow A'H = \dfrac{1}{6}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{{12}}\)
Xét tam giác vuông AA’H có: \(AH = AA'.\tan 60 = \dfrac{{a\sqrt 3 }}{{12}}.\sqrt 3 = \dfrac{a}{4}\)
Vậy \({V_{ABC.A'B'C'}} = AH.{S_{ABC}} = \dfrac{a}{4}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{16}}\)
Lăng trụ tam giác đều ABC.A’B’C’ có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng \({30^0}\). Điểm M nằm trên cạnh AA’. Biết cạnh $AB = a\sqrt 3 $, thể tích khối đa diện MBCC’B’ bằng
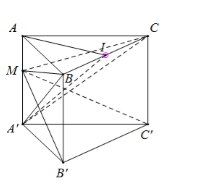
Gọi I là trung điểm BC ⇒ AI ⊥ BC⇒ BC ⊥ (AIA’)
Góc giữa (A’BC) và (ABC) là góc $\widehat {AIA'} = {30^0}$
$\begin{array}{*{20}{l}}{AI = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{3a}}{2}}\\{A'A = AI.\tan {{30}^\circ } = \dfrac{{a\sqrt 3 }}{2}}\end{array}$
Hình chóp M.BCC’B’ có diện tích đáy BCC’B’ là$S = BC.BB' = AB.A'A = \dfrac{{3{a^2}}}{2}$
Vì MA // BB’ nên MA // (BCC’B’) nên chiều cao của hình chóp M.BCC’B’ bằng khoảng cách từ A đến mặt phẳng (BCC’B’) và bằng $h = AI = \dfrac{{3a}}{2}$
Thể tích hình chóp là $V = \dfrac{1}{3}Sh = \dfrac{{3{a^3}}}{4}$
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại B với \(AB = a,AA' = 2a,\)\(A'C = 3a\) . Gọi M là trung điểm của \(A'C'\), I là giao điểm của đường thẳng AM và A’C. Tính theo a thể tích khối IABC .
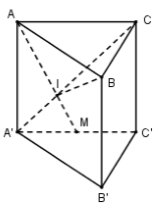
Ta có: \(A'M//AC \Rightarrow \dfrac{{A'M}}{{AC}} = \dfrac{{A'I}}{{IC}} = \dfrac{1}{2} \Rightarrow \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}\)
\(IA' \cap \left( {ABC} \right) = C \Rightarrow \dfrac{{d\left( {I;\left( {ABC} \right)} \right)}}{{d\left( {A';\left( {ABC} \right)} \right)}} = \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}\)
\(\dfrac{{{V_{I.ABC}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}d\left( {I;\left( {ABC} \right)} \right).{S_{ABC}}}}{{d\left( {A';\left( {ABC} \right)} \right).{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{2}{3} = \dfrac{2}{9} \Rightarrow {V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}}\)
$AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C$ vuông tại A\( \Rightarrow AC = \sqrt {A'{C^2} - AA{'^2}} = \sqrt {9{a^2} - 4{a^2}} = a\sqrt 5 \)
Xét tam giác vuông ABC có: $BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {5{a^2} - {a^2}} = 2a$
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2a.{a^2} = 2{a^3}\)
\( \Rightarrow {V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}} = \dfrac{2}{9}.2{a^3} = \dfrac{{4{a^3}}}{9}\)
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{a^3}\). Khi đó độ dài cạnh hình lập phương đã cho bằng
Độ dài cạnh hình lập phương đã cho bằng \(2a\).
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông \(ABC\) vuông tại \(A\), \(AC = a,\) \(\angle ACB = {60^0}\). Đường thẳng \(BC'\) tạo với mặt phẳng \(\left( {ACC'} \right)\) góc \({30^0}\). Tính thể tích khối lăng trụ \(ABC.A'B'C'\).
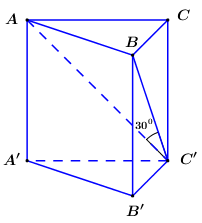
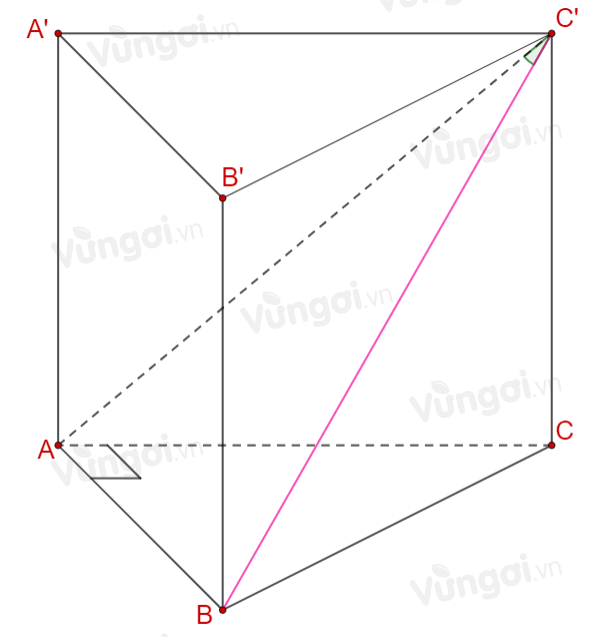
Xét tam giác vuông \(ABC\) ta có: \(AB = AC.\tan {60^0} = a\sqrt 3 \) \( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a\sqrt 3 .a = \dfrac{{\sqrt 3 {a^2}}}{2}\).
Ta có: \(\left\{ \begin{array}{l}AB \bot AC\\AB \bot AA'\end{array} \right. \Rightarrow AB \bot \left( {ACC'} \right)\) \( \Rightarrow \) \(AC'\) là hình chiếu vuông góc của \(BC'\) lên \(\left( {ACC'} \right)\).
\( \Rightarrow \angle \left( {BC';\left( {ACC'} \right)} \right) = \angle \left( {BC';AC'} \right) = \angle AC'B = {30^0}\).
Vì \(AB \bot \left( {ACC'} \right) \Rightarrow AB \bot AC' \Rightarrow \Delta ABC'\) vuông tại \(A\).
\(\begin{array}{l} \Rightarrow AC' = AB.\cot {30^0} = a\sqrt 3 .\sqrt 3 = 3a\\ \Rightarrow CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {9{a^2} - {a^2}} = 2a\sqrt 2 \end{array}\)
Vậy \({V_{ABC.A'B'C'}} = CC'.{S_{\Delta ABC}} = 2a\sqrt 2 .\dfrac{{\sqrt 3 {a^2}}}{2} = {a^3}\sqrt 6 \).
Đề thi THPT QG - 2021 - mã 102
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 4a\), góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^o}.\) Thể tích của khối hộp chữ nhật đã cho bằng
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(\left\{ \begin{array}{l}AO \bot BD\\AA' \bot BD\end{array} \right. \Rightarrow A'O \bot BD \Rightarrow \alpha = \left( {AO;A'O} \right) = \angle AOA' = {30^o}\)
Đáy \(ABCD\) là hình vuông có \(BD = 4a \Rightarrow AB = AD = 2a\sqrt 2 \)
Ta có: \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = 2a.\)
Trong \(\Delta AOA'\) có \(AA' = AO.\tan {30^o} = \dfrac{{2a\sqrt 3 }}{3}\)
Vậy thể tích khối hộp \(ABCD.A'B'C'D'\) là: \(V = 8{a^2}.\dfrac{{2a\sqrt 3 }}{3} = \dfrac{{16{a^3}\sqrt 3 }}{3}\)
Khối hộp chữ nhật có các kích thước lần lượt là \(a,2a,3a\) có thể tích bằng
Thể tích khối hộp chữ nhật là \(V = a.2a.3a = 6{a^3}\).
Công thức tính thể tích lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là:
Công thức tính thể tích lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là \(V = Sh\).
Thể tích khối hộp chữ nhật có diện tích đáy \(S\) và độ dài cạnh bên \(a\) là:
Hình hộp chữ nhật có cạnh bên vuông góc với đáy nên cạnh bên chính là đường cao.
Vì hình hộp chữ nhật cũng là hình lăng trụ nên thể tích của khối hộp cũng được tính bởi công thức \(V = Sh\), hay \(V = Sa\).
Đề thi THPT QG – 2021 lần 1– mã 104
Thể tích của khối lập phương cạnh \(2a\) bằng:
Thể tích khối lập phương cạnh \(2a\) là: \(V = {\left( {2a} \right)^3} = 8{a^3}\)

