Hàm số lũy thừa

Vì $\sqrt {2 - \sqrt 3 }  \notin \mathbb{Z} \Rightarrow$ Hàm số xác định $\Leftrightarrow {x^2} - 3x - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 4\\x <  - 1\end{array} \right.$.

Vậy TXĐ của hàm số là $D = \left( { - \infty ; - 1} \right) \cup \left( {4; + \infty } \right)$.

Hàm số $y = {x^5}$ xác định trên $\mathbb{R}$.

Hàm số $y = {x^{ - 1}}$ xác định nếu $x \ne 0$.

Hàm số $y = {x^{\sqrt 2 }}$ xác định nếu $x > 0$.

Hàm số $y = {\left( {{x^{\sqrt 2 }}} \right)^2}$ xác định nếu $x > 0$.

Vì hàm số $y = {x^{\dfrac{1}{n}}}$ có số mũ không nguyên nên cơ số phải dương, hay $x > 0$.

Ta có $\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}\,\,\left( {x > 0} \right)$ $\Rightarrow \left( {{x^{\frac{4}{3}}}} \right)' = \dfrac{4}{3}{x^{\frac{1}{3}}}$.

Ta có: $y = {\left( {2x} \right)^{\dfrac{5}{3}}}$$\Rightarrow y' = \dfrac{5}{3}\left( {2x} \right)'.{\left( {2x} \right)^{\dfrac{5}{3} - 1}} = \dfrac{{10}}{3}{\left( {2x} \right)^{\dfrac{2}{3}}}$.

Ta có: $\left( {\sqrt[n]{x}} \right)' = \left( {{x^{\dfrac{1}{n}}}} \right)' = \dfrac{1}{n}{x^{\dfrac{1}{n} - 1}} = \dfrac{1}{n}{x^{\dfrac{{1 - n}}{n}}} = \dfrac{1}{n}{x^{ - \dfrac{{n - 1}}{n}}}$

Hàm số $y = {x^{ - 4}}$ có tập xác định là $\mathbb{R}\backslash \left\{ 0 \right\}$ và có $y' =  - 4{x^{ - 5}}$ nên không đồng biến trên các khoảng xác định (đồng biến trên $\left( { - \infty ,0} \right)$ và nghịch biến trên $\left( {0, + \infty } \right)$), loại A.

Hàm số $y = {x^{ - \dfrac{3}{4}}}$ có tập xác định là $\left( {0, + \infty } \right)$ và có $y' =  - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)$ nên không đồng biến trên từng khoảng xác định, loại B.

Hàm số $y = {x^4}$ có tập xác định là $\mathbb{R}$ và có $y' = 4{x^3}$ nên không đồng biến trên các khoảng xác định, loại C.

Hàm số $y = \sqrt[3]{x}$ có tập xác định là $\mathbb{R}$ và có $y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0$ nên hàm số đồng biến trên các khoảng xác định.

Khi $\alpha  = 0$ thì $y = 1$ nên đồ thị hàm số là đường thẳng.

Khi $\alpha  = 1$ thì $y = x$ nên đồ thị hàm số là đường thẳng.

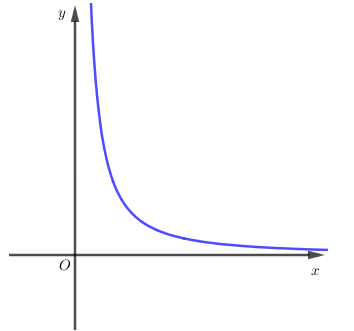
Quan sát hình vẽ các dáng đồ thị của hàm số lũy thừa ta thấy điều kiện của $\alpha$ ứng với các đồ thị bài cho là $\alpha  < 0$.

Tập xác định của hàm số $y=x^\alpha$ phụ thuộc vào $\alpha$ nên chưa chắc là $D = \left( {0; + \infty } \right)$ vì:

+ Tập xác định của hàm số là $D = \left( {0; + \infty } \right)$ khi $\alpha$ không nguyên.

+ Khi $\alpha  \in {\mathbb{N}^*}$ thì $D = \mathbb{R},\alpha  \in \mathbb{Z}\backslash {\mathbb{N}^*}$ thì $D = \mathbb{R}\backslash \left\{ 0 \right\}$.

Do $\sqrt 5$ không nguyên nên điều kiện xác định của hàm số này là $2 - 3x > 0 \Leftrightarrow x < \dfrac{2}{3}.$

Tập xác định $D = \left( { - \infty ;\dfrac{2}{3}} \right).$

Ta có: ${f_1}(x)$ và ${f_2}(x)$ là hai hàm số căn bậc chẵn nên có tập xác định là $\left[ {0; + \infty } \right).$

${f_3}(x)$ và ${f_4}(x)$ là hai hàm số mũ với số mũ không nguyên nên có tập xác định là $\left( {0; + \infty } \right).$

Điều kiện xác định của hàm số $y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}$ là: ${x^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 2\\x > 2\end{array} \right.$.

Suy ra tập xác định của hàm số là: $D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)$.

Điều kiện: ${x^2} - x - 6 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 3\\x \ne  - 2\end{array} \right.$.

Điều kiện: ${x^2} - 1 \ne 0$$\Leftrightarrow x \ne  \pm 1$.

Đây là hàm với số mũ nguyên âm nên điều kiện là ${x^3} - 6{x^2} + 11x - 6 \ne 0 \Leftrightarrow x \in \mathbb{R}\backslash \left\{ {1;2;3} \right\}$.

Với $x > 0$ thì $f\left( x \right) = {x^{\dfrac{1}{3} + \dfrac{1}{4} + \dfrac{5}{{12}}}} = x$ nên $f\left( {2,7} \right) = 2,7$.

Với $x > 0$ thì $f\left( x \right) = {x^{2 + \dfrac{2}{3}}} = {x^{\dfrac{8}{3}}} \Rightarrow f'\left( x \right) = \dfrac{8}{3}{x^{\dfrac{5}{3}}}$ nên $f'\left( 1 \right) = \dfrac{8}{3}$.

ĐK: $0 < x \ne 1$.

Ta có ${x^{{{\log }_\alpha }\left( {\alpha x} \right)}} \ge {(\alpha x)^4} \Leftrightarrow {x^{{{\log }_\alpha }x + 1}} \ge {\left( {\alpha x} \right)^4}$.

Đặt $t = {\log _\alpha }x \Rightarrow x = {\alpha ^t}$. Khi đó bất phương trình trở thành: ${\left( {{\alpha ^t}} \right)^{t + 1}} \ge {\left( {\alpha .{\alpha ^t}} \right)^4}$.

$\Leftrightarrow {\alpha ^{{t^2} + t}} \ge {\alpha ^{4t + 4}} \Leftrightarrow {t^2} + t \le 4t + 4 \Leftrightarrow {t^2} - 3t - 4 \le 0$.

$\Leftrightarrow  - 1 \le t \le 4$.

$\Rightarrow  - 1 \le {\log _\alpha }x \le 4 \Leftrightarrow {\alpha ^4} \le x \le \dfrac{1}{\alpha }$ (thoả mãn điều kiện).

Ta có $y = {\left( {1 - \cos 3x} \right)^6} \Rightarrow y = 6{\left( {1 - \cos 3x} \right)^5}.\left( {1 - \cos 3x} \right)'$.

$= 6{\left( {1 - \cos 3x} \right)^5}.3\sin 3x = 18\sin 3x{\left( {1 - \cos 3x} \right)^5}.$