Hàm số lũy thừa

$y' = \left( {\sqrt {1 - x} } \right)'{.2^{\sqrt {1 - x} }}.\ln 2 = \dfrac{{ - \ln 2}}{{2\sqrt {1 - x} }}{2^{\sqrt {1 - x} }}$.

Ta có $y' = \pi {x^{\pi  - 1}} \Rightarrow y'' = \pi \left( {\pi  - 1} \right){x^{\pi  - 2}}$ do đó $y''\left( 1 \right) = \pi \left( {\pi  - 1} \right).$.

Ta có: $\sqrt[5]{{{{\left( {{x^2} + 1} \right)}^2}}} = {\left( {{x^2} + 1} \right)^{\dfrac{2}{5}}}$

Do đó $\left[ {{{\left( {{x^2} + 1} \right)}^{\dfrac{2}{5}}}} \right]' = \dfrac{2}{5}.{\left( {{x^2} + 1} \right)^{\dfrac{2}{5} - 1}}.\left( {{x^2} + 1} \right)'$ $= \dfrac{2}{5}{\left( {{x^2} + 1} \right)^{ - \dfrac{3}{5}}}.2x = \dfrac{4}{5}x.\dfrac{1}{{{{\left( {{x^2} + 1} \right)}^{\dfrac{3}{5}}}}} = \dfrac{{4x}}{{5\sqrt[5]{{{{\left( {{x^2} + 1} \right)}^3}}}}}$

Ta có: $y' = \left( {{{\left( {{x^2} + 1} \right)}^{\dfrac{e}{2}}}} \right)' = \dfrac{e}{2}.2x{\left( {{x^2} + 1} \right)^{\dfrac{e}{2} - 1}} = ex{\left( {{x^2} + 1} \right)^{\dfrac{e}{2} - 1}} = ex\sqrt {{{\left( {{x^2} + 1} \right)}^{e - 2}}}$.

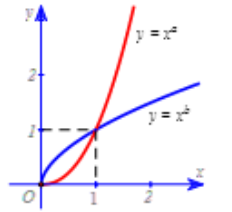
Dựa vào đồ thị ta có đồ thị hàm số $y = {x^a}$ ứng với $a > 1,$ đồ thị hàm số $y = {x^b}$ ứng với $0 < b < 1.$

Do đó $0 < b < 1 < a$.

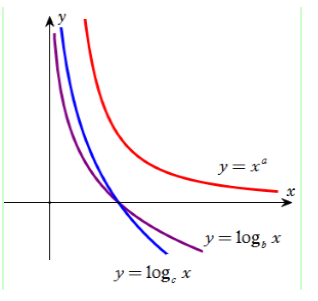
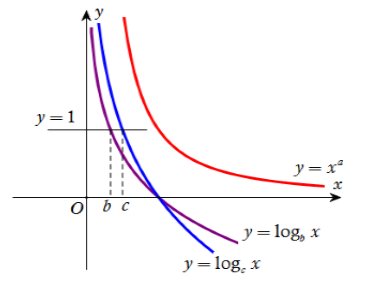
Nhận thấy hàm số $y = {x^a}$ nghịch biến $\Rightarrow a < 0.$ Do đó ta loại ngay đáp án C và D (vì $b,{\rm{ }}c$ là các số thực dương khác $1$).

Kẻ đường thẳng $y = 1$ cắt đồ thị của hai hàm số $G$, $A\left( {1; - 1; - 2} \right)$ lần lượt tại điểm có hoành độ là $x = b$ và $x = c$ như hình vẽ. Dựa vào hình vẽ ta thấy $0 < b < c.$

Vậy $a < b < c.$

Ta có: $\left( {{x^{\frac{5}{3}}}} \right)' = \dfrac{5}{3}.{x^{\frac{2}{3}}}$

Ta có: $f\left( x \right) = {x^2}\sqrt[3]{{{x^2}}} = {x^2}.{x^{\frac{2}{3}}} = {x^{\frac{8}{3}}}$.

$\Rightarrow f'\left( x \right) = \dfrac{8}{3}.{x^{\frac{5}{3}}} \Rightarrow f\left( 1 \right) = \dfrac{8}{3}$.

$\begin{array}{l}y = \dfrac{1}{{\sqrt[3]{{{x^2} + x + 1}}}} = {\left( {{x^2} + x + 1} \right)^{ - \frac{1}{3}}}\\ \Rightarrow y' =  - \dfrac{1}{3}.{\left( {{x^2} + x + 1} \right)^{ - \frac{1}{3} - 1}}.\left( {{x^2} + x + 1} \right)'\\\,\,\,\,\,\,y' =  - \dfrac{1}{3}{\left( {{x^2} + x + 1} \right)^{ - \frac{4}{3}}}.\left( {2x + 1} \right)\\\,\,\,\,\,\,y' = \dfrac{{ - 2x - 1}}{{3{{\left( {\sqrt[3]{{{x^2} + x + 1}}} \right)}^4}}}\\\,\,\,\,\,\,y' = \dfrac{{ - 2x - 1}}{{3\left( {{x^2} + x + 1} \right)\sqrt[3]{{{x^2} + x + 1}}}}\end{array}$

Hàm số $y = {\left( {\dfrac{{2x - 1}}{x}} \right)^{10}}$xác định khi và chỉ khi $\dfrac{{2x - 1}}{x}$ xác định $\Leftrightarrow x \ne 0$.

Vậy TXĐ của hàm số là $D = \mathbb{R}\backslash \left\{ 0 \right\}$.

Vì $2017 \in {\mathbb{Z}^ + }$ nên hàm số xác định khi và chỉ khi $2x - \sqrt {x + 4}$ xác định $\Leftrightarrow x \ge  - 4$.

Vậy $D = \left[ { - 4; + \infty } \right)$.

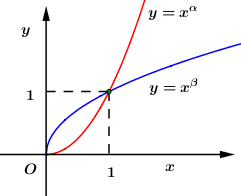
Dựa vào đồ thị hàm số ta thấy hàm số $y = {x^\alpha }$ là hàm số đồng biến trên $\left( {0; + \infty } \right) \Rightarrow \alpha  > 1.$

Hàm số $y = {x^\beta }$ nghịch biến trên $\left( {0; + \infty } \right) \Rightarrow 0 < \beta  < 1.$

$\Rightarrow 0 < \beta  < 1 < \alpha .$

TXĐ : $D = \left[ {0; + \infty } \right)$

Ta có :   

$\begin{array}{l}f\left( x \right) = m.\sqrt[3]{x} + \sqrt x  = m.{x^{\dfrac{1}{3}}} + {x^{\dfrac{1}{2}}}\\ \Rightarrow f'\left( x \right) = m.\dfrac{1}{3}.{x^{\dfrac{1}{3} - 1}} + \dfrac{1}{2}.{x^{\dfrac{1}{2} - 1}}\\ \Leftrightarrow f'\left( x \right) = \dfrac{1}{3}m.{x^{ - \dfrac{2}{3}}} + \dfrac{1}{2}.{x^{ - \dfrac{1}{2}}}\\ \Leftrightarrow f'\left( x \right) = \dfrac{m}{{3.\sqrt[3]{{{x^2}}}}} + \dfrac{1}{{2\sqrt x }}\end{array}$

Theo giả thiết,$f'\left( 1 \right) = \dfrac{3}{2}$ nên ta có :

$\begin{array}{l}\dfrac{m}{{3.\sqrt[3]{{{1^2}}}}} + \dfrac{1}{{2\sqrt 1 }} = \dfrac{3}{2}\\ \Leftrightarrow \dfrac{m}{3} + \dfrac{1}{2} = \dfrac{3}{2} \Rightarrow m = 3\end{array}$

Vậy $m = 3$

$\begin{array}{l}y = {\left( {\dfrac{{2018}}{x}} \right)^{2019}}.{\left( {\dfrac{x}{{2019}}} \right)^{2018}} = \dfrac{{{{2018}^{2019}}.{x^{2018}}}}{{{x^{2019}}{{.2019}^{2018}}}} = \dfrac{{{{2018}^{2019}}}}{{{{2019}^{2018}}}}.\dfrac{1}{x}\\ \Rightarrow y' = \dfrac{{{{2018}^{2019}}}}{{{{2019}^{2018}}}}.\left( { - \dfrac{1}{{{x^2}}}} \right) \Rightarrow y'\left( 1 \right) =  - \dfrac{{{{2018}^{2019}}}}{{{{2019}^{2018}}}}\end{array}$

Ta có $\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}\,\,\left( {x > 0} \right)$ $\Rightarrow \left( {{x^{\frac{5}{2}}}} \right)' = \dfrac{5}{2}{x^{\frac{3}{2}}}$.

Ta có: $\left( {{x^{\frac{5}{4}}}} \right)' = \dfrac{5}{4}.{x^{\frac{1}{4}}}$

Vì $-6$ là số nguyên âm nên:

Hàm số $y = {\left( {x - 3} \right)^{ - 6}}$ xác định khi $x - 3 \ne 0 \Leftrightarrow x \ne 3$

Vậy TXĐ của hàm số là $\mathbb{R}\backslash \left\{ 3 \right\}$.

+ Hàm số $y = {\left( {{x^2} + 1} \right)^{\dfrac{1}{2}}}$ có điều kiện xác định ${x^2} + 1 > 0$ (luôn đúng) nên TXĐ: $D = \mathbb{R}$

+ Hàm số $y = \sqrt {{x^2}}$ có điều kiện xác định ${x^2} \ge 0$ (luôn đúng) nên TXĐ: $D = \mathbb{R}$

+ Hàm số $y = \dfrac{x}{{x - 1}}$ có điều kiện xác định  $x - 1 \ne 0 \Leftrightarrow x \ne 1$ nên TXĐ: $D = \mathbb{R}\backslash \left\{ 1 \right\}$

+ Hàm số $y = \sqrt[3]{x}$  xác định với mọi $x$ nên TXĐ: $D = \mathbb{R}$

Hàm số lũy thừa là hàm số có số mũ là số thực.

Do $\dfrac{1}{5} \notin \mathbb{R} \Rightarrow$ Hàm số xác định $\Leftrightarrow 4 - {x^2} > 0 \Leftrightarrow  - 2 < x < 2$.

Vậy TXĐ của hàm số là $D = \left( { - 2;2} \right)$.