Biết \({x_1}\), \({x_2}\) là hai nghiệm của phương trình \({\log _7}\left( {\dfrac{{4{x^2} - 4x + 1}}{{2x}}} \right) + 4{x^2} + 1 = 6x\) và \(x{{\kern 1pt} _1} + 2{x_2} = \dfrac{1}{4}\left( {a + \sqrt b } \right)\) với \(a\), \(b\) là hai số nguyên dương. Tính \(a + b.\)
Điều kiện \(\left\{ \begin{array}{l}x > 0\\x \ne \dfrac{1}{2}\end{array} \right.\)
Ta có \({\log _7}\left( {\dfrac{{4{x^2} - 4x + 1}}{{2x}}} \right) + 4{x^2} + 1 = 6x \Leftrightarrow {\log _7}\left( {\dfrac{{{{\left( {2x - 1} \right)}^2}}}{{2x}}} \right) + 4{x^2} - 4x + 1 = 2x\)
\( \Leftrightarrow {\log _7}{\left( {2x - 1} \right)^2} + {\left( {2x - 1} \right)^2} = {\log _7}2x + 2x\left( 1 \right)\)
Xét hàm số \(f\left( t \right) = {\log _7}t + t \Leftrightarrow f'\left( t \right) = \dfrac{1}{{t\ln 7}} + 1 > 0\) với \(t > 0\)
Vậy hàm số đồng biến
Phương trình \(\left( 1 \right)\) trở thành \(f\left( {{{\left( {2x - 1} \right)}^2}} \right) = f\left( {2x} \right) \Leftrightarrow {\left( {2x - 1} \right)^2} = 2x \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{3 + \sqrt 5 }}{4}\\x = \dfrac{{3 - \sqrt 5 }}{4}\end{array} \right.\)
Vậy \({x_1} + 2{x_2} = \left[ \begin{array}{l}\dfrac{{9 - \sqrt 5 }}{4}{\rm{ }}\left( l \right)\\\dfrac{{9 + \sqrt 5 }}{4}{\rm{ }}\left( {tm} \right)\end{array} \right. \Rightarrow a = 9;b = 5 \Rightarrow a + b = 9 + 5 = 14.\)
Tính tích tất cả các nghiệm thực của phương trình \({\log _2}\left( {\dfrac{{2{x^2} + 1}}{{2x}}} \right) + {2^{\left( {x + \frac{1}{{2x}}} \right)}} = 5\).
Điều kiện: \(x > 0\).
PT: \( \Leftrightarrow {\log _2}\left( {\dfrac{{2{x^2} + 1}}{{2x}}} \right) + {2^{\left( {\frac{{2{x^2} + 1}}{{2x}}} \right)}} = 5\,\,\,\,\,\left( 1 \right)\).
Đặt \(t = \dfrac{{2{x^2} + 1}}{{2x}} = x + \dfrac{1}{{2x}} \ge 2\sqrt {x.\dfrac{1}{{2x}}} = \sqrt 2 \)
PT trở thành \({\log _2}t + {2^t} = 5{\rm{ (2)}}\).
Xét hàm \(f\left( t \right) = {\log _2}t + {2^t}\,\,\left( {t \ge \sqrt 2 } \right)\) là hàm đồng biến nên:
\(\left( 2 \right) \Leftrightarrow f\left( t \right) = f\left( 2 \right) \Leftrightarrow t = 2\)(t/m).
Với \(t = 2\) thì \(\dfrac{{2{x^2} + 1}}{{2x}} = 2 \Leftrightarrow 2{x^2} - 4x + 1 = 0\)
Vậy \({x_1}{x_2} = \dfrac{1}{2}\) (theo Viet ).
Cho \(a\), \(b\), \(c\) là các số thực thuộc đoạn \(\left[ {1;2} \right]\) thỏa mãn \(\log _2^3a + \log _2^3b + \log _2^3c \le 1.\) Khi biểu thức \(P = {a^3} + {b^3} + {c^3} - 3\left( {{{\log }_2}{a^a} + {{\log }_2}{b^b} + {{\log }_2}{c^c}} \right)\) đạt giá trị lớn nhất thì giá trị của tổng.
\(a + b + c\) là
Đặt \(x = {\log _2}a;y = {\log _2}b;z = {\log _2}c.\)
Vì \(a,b,c \in \left[ {1;\,2} \right]\) nên \(x,y,z \in \left[ {0;1} \right]\)
\(\begin{array}{l}P = {a^3} + {b^3} + {c^3} - 3\left( {{{\log }_2}{a^a} + {{\log }_2}{b^b} + {{\log }_2}{c^c}} \right)\\= {a^3} + {b^3} + {c^3} - 3\left( {a{{\log }_2}a + b{{\log }_2}b + c{{\log }_2}c} \right)\\= {a^3} + {b^3} + {c^3} - 3\left( {ax + by + cz} \right).\end{array}\)
Ta chứng minh \({a^3} - 3ax \le {x^3} + 1.\) Thật vậy:
Xét hàm số \(f\left( a \right) = a - {\log _2}a,\,a \in \left[ {1;\,\,2} \right] \Rightarrow f'\left( a \right) = 1 - \dfrac{1}{{a\ln 2}} \Rightarrow f'\left( a \right) = 0 \Leftrightarrow a = \dfrac{1}{{\ln 2}}\)
Trên đoạn \(\left[ {1;2} \right]\) ta có \(f\left( a \right) \le \max \left\{ {f\left( 1 \right),f\left( 2 \right),f\left( {\dfrac{1}{{\ln 2}}} \right)} \right\} = 1 \Rightarrow a - {\log _2}a \le 1\)
hay \(a - x \le 1 \Leftrightarrow a - x - 1 \le 0.\)
Xét: ${a^3} - 3ax - {x^3} - 1 = \left( {a - x - 1} \right)\left( {{a^2} + {x^2} + 1 + a + ax - x} \right) \le 0$
( Vì theo trên ta có \(a - x - 1 \le 0\) và \({a^2} + \left( {{x^2} - x + 1} \right) + a + ax > 0,\) \(\forall a \in \left[ {1;\,\,2} \right],\,\) \(\forall x \in \left[ {0;\,\,1} \right]\))
Vậy \({a^3} - 3ax - {x^3} - 1 \le 0\)\( \Leftrightarrow {a^3} - 3ax \le {x^3} + 1\). Tương tự \({b^3} - 3by \le {y^3} + 1;\)\({c^3} - 3cz \le {z^3} + 1\)
Do đó \(P\, = {a^3} + {b^3} + {c^3} - 3\left( {ax + by + cz} \right)\, \le {x^3} + {y^3} + {z^3} + 3 \le 1 + 3 = 4\)
Dấu bằng xảy ra khi và chỉ khi
\(\left\{ \begin{array}{l}f\left( a \right) = \max \left\{ {f\left( 1 \right),f\left( 2 \right),f\left( {\dfrac{1}{{\ln 2}}} \right)} \right\} = 1\\f\left( b \right) = \max \left\{ {f\left( 1 \right),f\left( 2 \right),f\left( {\dfrac{1}{{\ln 2}}} \right)} \right\} = 1\\f\left( b \right) = \max \left\{ {f\left( 1 \right),f\left( 2 \right),f\left( {\dfrac{1}{{\ln 2}}} \right)} \right\} = 1\\{x^3} + {y^3} + {z^3} = 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 1\\a = 2\end{array} \right.\\\left[ \begin{array}{l}b = 1\\b = 2\end{array} \right.\\\left[ \begin{array}{l}c = 1\\c = 2\end{array} \right.\\{x^3} + {y^3} + {z^3} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\\\left[ \begin{array}{l}y = 0\\y = 1\end{array} \right.\\\left[ \begin{array}{l}z = 0\\z = 1\end{array} \right.\\{x^3} + {y^3} + {z^3} = 1\end{array} \right.\)
Với \(x = 0 \Rightarrow {y^3} + {z^3} = 1\). Nếu \(y = 0\) thì \({\rm{z}} = 1\), nếu \(y = 1\) thì \({\rm{z}} = 0\)
Với \(x = 1 \Rightarrow {y^3} + {z^3} = 0 \Rightarrow y = z = 0\)( Vì y và z chỉ có thể bằng 0 hoặc bằng 1)
Vậy đẳng thức xảy ra khi và chỉ khi \(x = y = 0,z = 1\) và các hoán vị, tức là \(a = b = 1,c = 2\) và các hoán vị. Khi đó \(a + b + c = 4\).
Cho $m = {\log _a}\sqrt {ab} $ với $a,b > 1$ và $P = \log _a^2b + 54{\log _b}a$. Khi đó giá trị của $m$ để $P$ đạt giá trị nhỏ nhất là:
Ta có $P = \log _a^2b + 54{\log _b}a = \log _a^2b + \dfrac{{54}}{{{{\log }_a}b}}$
Đặt $t = {\log _a}b$ thì $P = {t^2} + \dfrac{{54}}{t}$
Vì \(a,\,\,b > 1\) nên $t = {\log _a}b > 0$.
Áp dụng bất đẳng thức Cô – si ta có
$P = {t^2} + \dfrac{{54}}{t} = {t^2} + \dfrac{{27}}{t} + \dfrac{{27}}{t} \ge 3\sqrt[3]{{{{27}^2}}} = 27.$
Đẳng thức xảy ra khi và chỉ khi ${t^2} = \dfrac{{27}}{t} \Leftrightarrow t = 3.$
Ta có $m = {\log _a}\sqrt {ab} = \dfrac{1}{2}{\log _a}\left( {ab} \right)$$ = \dfrac{1}{2}\left( {1 + {{\log }_a}b} \right) = \dfrac{1}{2}\left( {1 + t} \right) = \dfrac{1}{2}\left( {1 + 3} \right) = 2$
Tìm số giá trị nguyên của \(m\) để phương trình \({4^{x + 1}} + {4^{1 - x}} = \left( {m + 1} \right)\left( {{2^{2 + x}} - {2^{2 - x}}} \right) + 16 - 8m\) có nghiệm trên \(\left[ {0;1} \right]\) ?
\({4^{x + 1}} + {4^{1 - x}} = \left( {m + 1} \right)\left( {{2^{2 + x}} - {2^{2 - x}}} \right) + 16 - 8m\)\( \Leftrightarrow 4\left( {{4^x} + {4^{ - x}}} \right) = 4\left( {m + 1} \right)\left( {{2^x} - {2^{ - x}}} \right) + 16 - 8m\)
Đặt \(t = u\left( x \right) = {2^x} - {2^{ - x}}\), \(x \in \left[ {0;\,1} \right]\)
Ta có: \(u'\left( x \right) = {2^x}\ln 2 + {2^{ - x}}\ln 2 > 0,\) \(\forall x \in \left[ {0;\,1} \right]\)
Suy ra \(u\left( 0 \right) \le t \le u\left( 1 \right)\) hay \(t \in \left[ {0;\dfrac{3}{2}} \right]\)
\( \Rightarrow {t^2} = {4^x} + {4^{ - x}} - {2.2^x}{.2^{ - x}} \Rightarrow {4^x} + {4^{ - x}} = {t^2} + 2\)
Phương trình trở thành :
$4\left( {{t^2} + 2} \right) = 4t\left( {m + 1} \right) + 16 - 8m$$ \Leftrightarrow {t^2} + 2 = t\left( {m + 1} \right) + 4 - 2m$
$ \Leftrightarrow {t^2} + 2 = mt + t + 4 - 2m$$ \Leftrightarrow {t^2} - t - 2 = m\left( {t - 2} \right)$$ \Leftrightarrow m = \dfrac{{{t^2} - t - 2}}{{t - 2}} = t + 1$
Vì \(t \in \left[ {0;\;\;\dfrac{3}{2}} \right]\) nên \(m = t + 1 \in \left[ {1;\dfrac{5}{2}} \right]\)
Vậy có \(2\) giá trị của \(m\) thỏa mãn.
Xét bất phương trình \(\log _2^22x - 2\left( {m + 1} \right){\log _2}x - 2 < 0\). Tìm tất cả các giá trị của tham số \(m\) để bất phương trình có nghiệm thuộc khoảng \(\left( {\sqrt {2;} + \infty } \right)\).
Điều kiện: \(x > 0\)
\(\log _2^2 2x - 2\left( {m + 1} \right){\log _2}x - 2 < 0\)
\( \Leftrightarrow {\left( {1 + {{\log }_2}x} \right)^2} - 2\left( {m + 1} \right){\log _2}x - 2 < 0{\rm{ }}\left( 1 \right)\).
Đặt \(t = {\log _2}x\). Vì $x > \sqrt 2 $ nên ${\log _2}x > {\log _2}\sqrt 2 = \dfrac{1}{2}$.
Do đó $t \in \left( {\dfrac{1}{2}; + \infty } \right)$
\(\left( 1 \right)\) thành \({\left( {1 + t} \right)^2} - 2\left( {m + 1} \right)t - 2 < 0\)\( \Leftrightarrow {t^2} - 2mt - 1 < 0\) \(\left( 2 \right)\)
Yêu cầu bài toán tương đương tìm \(m\) để bpt $(2)$ có nghiệm thuộc \(\left( {\dfrac{1}{2}; + \infty } \right)\).
Xét bất phương trình $(2)$ có: $\Delta ' = {m^2} + 1 > 0,{\rm{ }}\forall m \in \mathbb{R}$.
\(f\left( t \right) = {t^2} - 2mt - 1 = 0\) có \(ac < 0\) nên $f(t)$ luôn có $2$ nghiệm phân biệt \({t_1} < 0 < {t_2}\) nên tập nghiệm của $(2)$ là $(t_1;t_2)$
Khi đó cần \(\dfrac{1}{2} < {t_2} \Leftrightarrow m + \sqrt {{m^2} + 1} > \dfrac{1}{2} \Leftrightarrow m > - \dfrac{3}{4}\)
Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty Bảo Việt với thể lệ như sau: Cứ đến tháng $9$ hàng năm người đó đóng vào công ty là $12$ triệu đồng với lãi suất hàng năm không đổi là $6\% $ / năm. Hỏi sau đúng $18$ năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân.
Gọi số tiền đóng hàng năm là $A = 12$ (triệu đồng), lãi suất là $r = 6\% = 0,06$.
Sau \(1\) năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là \({A_1} = A\left( {1 + r} \right)\). (nhưng người đó không rút mà lại đóng thêm $A$ triệu đồng nữa, nên số tiền gốc để tính lãi năm sau là \({A_1} + A\)).
Sau \(2\) năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\({A_2} = \left( {{A_1} + A} \right)\left( {1 + r} \right) = \left[ {A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right) = A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\)
Sau \(3\) năm, nếu người đó đi rút tiền thì sẽ nhận được số tiền là:
\({A_3} = \left( {{A_2} + A} \right)\left( {1 + r} \right) = \left[ {A{{\left( {1 + r} \right)}^2} + A\left( {1 + r} \right) + A} \right]\left( {1 + r} \right) = A{\left( {1 + r} \right)^3} + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)\)
…
Sau \(18\) năm, người đó đi rút tiền thì sẽ nhận được số tiền là:
${A_{18}} = A{\left( {1 + r} \right)^{18}} + A{\left( {1 + r} \right)^{17}} + ... + A{\left( {1 + r} \right)^2} + A\left( {1 + r} \right)$
Tính: ${A_{18}} = A\left[ {{{\left( {1 + r} \right)}^{18}} + {{\left( {1 + r} \right)}^{17}} + ... + {{\left( {1 + r} \right)}^2} + \left( {1 + r} \right) + 1 - 1} \right]$
$ \Rightarrow {A_{18}} = A\left[ {\dfrac{{{{\left( {1 + r} \right)}^{19}} - 1}}{{\left( {1 + r} \right) - 1}} - 1} \right] = A\left[ {\dfrac{{{{\left( {1 + r} \right)}^{19}} - 1}}{r} - 1} \right] = 12\left[ {\dfrac{{{{\left( {1 + 0,06} \right)}^{19}} - 1}}{{0,06}} - 1} \right] \approx 393,12$
Cho hai số thực $a$, $b$ thỏa mãn $a > b > \dfrac{4}{3}$ và biểu thức $P = 16{\log _a}\left( {\dfrac{{{a^3}}}{{12b - 16}}} \right) + 3\log _{\frac{a}{b}}^2a$ có giá trị nhỏ nhất. Tính $a + b.$
Ta có: $P = 16{\log _a}\left( {\dfrac{{{a^3}}}{{12b - 16}}} \right) + 3\log _{\frac{a}{b}}^2a$. Vì số hạng thứ hai chứa ${\log _{\frac{a}{b}}}a$ nên ta cố gắng đưa ${\log _a}\left( {\dfrac{{{a^3}}}{{12b - 16}}} \right)$ về ${\log _a}\dfrac{a}{b}$. Điều này buộc ta cần đánh giá $12b - 16 \le {b^3}$. Thật vậy:
Ta có: $12b - 16 \le {b^3} \Leftrightarrow {\left( {b - 2} \right)^2}\left( {b + 4} \right) \ge 0$ (Đúng).
Suy ra: $\dfrac{{{a^3}}}{{12b - 16}} \ge \dfrac{a}{b} > 1$ $ \Rightarrow {\log _a}\left( {\dfrac{{{a^3}}}{{12b - 16}}} \right) \ge {\log _a}{\left( {\dfrac{a}{b}} \right)^3} = 3{\log _a}\dfrac{a}{b} > 0$
Do đó:
$P \ge 48{\log _a}\dfrac{a}{b} + 3\log _{\frac{a}{b}}^2a$ $ = 3\left( {8{{\log }_a}\dfrac{a}{b} + 8{{\log }_a}\dfrac{a}{b} + \log _{\frac{a}{b}}^2a} \right)$
Áp dụng bất đẳng thức Cauchy cho $3$ số dương $8{\log _a}\dfrac{a}{b}$, $8{\log _a}\dfrac{a}{b}$, $\log _{\frac{a}{b}}^2a$ ta được:
$P \ge 3 \cdot 3 \cdot \sqrt[3]{{\left( {8{{\log }_a}\dfrac{a}{b} \cdot 8{{\log }_a}\dfrac{a}{b} \cdot \log _{\frac{a}{b}}^2a} \right)}} = 9\sqrt[3]{{64}} = 36.$
Đẳng thức xảy ra khi và chỉ khi
$\left\{ \begin{array}{l}b = 2\\8{\log _a}\dfrac{a}{b} = \log _{\frac{a}{b}}^2a = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2\\{\log _a}\dfrac{a}{b} = \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2\\{\log _a}2 = \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2\\a = 4\end{array} \right..$
Vậy $a + b = 6.$
Giá trị nào của \(m\) để phương trình \(\log _3^2x + \sqrt {\log _3^2x + 1} - 2m - 1 = 0\) có ít nhất một nghiệm thuộc đoạn \(\left[ {1\,;\,\,{3^{\sqrt 3 }}} \right]\).
Điều kiện \(x > 0\).
Đặt \(t = \sqrt {\log _3^2x + 1} \ge 1\), ta được phương trình \({t^2} + t - 2m - 2 = 0\,\,\,\left( * \right)\)
Ta có \(x \in \left[ {1\,;\,\,{3^{\sqrt 3 }}} \right]\) \( \Leftrightarrow \) \(0 \le {\log _3}x \le \sqrt 3 \) \( \Leftrightarrow \) \(1 \le t = \sqrt {\log _3^2x + 1} \le 2\).
Phương trình đã cho có nghiệm $x \in \left[ {1\,;\,\,{3^{\sqrt 3 }}} \right]$ $\Leftrightarrow$ \(\left( * \right)\) có nghiệm \(t \in \left[ {1\,;\,2} \right]\).
Đặt \(f\left( t \right) = {t^2} + t\), với \(t \in \left[ {1\,;\,\,2} \right]\).
Hàm số \(f\left( t \right)\) là hàm đồng biến trên đoạn \(\left[ {1\,;\,\,2} \right]\).
Ta có \(f\left( 1 \right) = 2\) và \(f\left( 2 \right) = 6\).
Phương trình \({t^2} + t = 2m + 2\) \( \Leftrightarrow \) \(f\left( t \right) = 2m + 2\) có nghiệm \(t \in \left[ {1\,;\,\,2} \right]\) \( \Leftrightarrow \) \(f\left( 1 \right) \le 2m + 2 \le f\left( 2 \right)\)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}f\left( 1 \right) \le 2m + 2\\2m + 2 \le f\left( 2 \right)\end{array} \right.\) \( \Leftrightarrow \) \(\left\{ \begin{array}{l}2 \le 2m + 2\\2m + 2 \le 6\end{array} \right.\) \( \Leftrightarrow \) \(0 \le m \le 2\).
Tìm \(m\) để tồn tại duy nhất cặp \(\left( {x;\,y} \right)\) thỏa mãn \({\log _{{x^2} + {y^2} + 2}}\left( {4x + 4y - 4} \right) \ge 1\) và \({x^2} + {y^2} + 2x - 2y + 2 - m = 0\).
Điều kiện \(4x + 4y - 4 > 0\)
Ta có \({\log _{{x^2} + {y^2} + 2}}\left( {4x + 4y - 4} \right) \ge 1\) \( \Leftrightarrow 4x + 4y - 4 \ge {x^2} + {y^2} + 2\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} \le 2\,\,\,\,\left( {{C_1}} \right)\)
Miền nghiệm của bất phương trình là hình tròn (cả bờ) \(\left( {{C_1}} \right)\) có tâm \({I_1}\,\left( {2;\,\,2} \right)\) bán kính \({R_1} = \sqrt 2 \)
Mặt khác: \({x^2} + {y^2} + 2x - 2y + 2 - m = 0\)\( \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = m\,\,\,\left( * \right)\)
Với \(m = 0\) \( \Rightarrow x = - 1;\,\,y = 1\) không thỏa mãn: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} \le 2\).
Với \(m > 0\) thì \(\,\left( * \right)\) là đường tròn\(\,\left( {{C_2}} \right)\) có tâm \({I_2}\,\left( { - 1;\,\,1} \right)\) bán kính \({R_2} = \sqrt m \).
Để tồn tại duy nhất cặp \(\left( {x;\,y} \right)\) thì \(\,\left( {{C_1}} \right)\) và \(\,\left( {{C_2}} \right)\) tiếp xúc với nhau.
Trường hợp 1: \(\,\left( {{C_1}} \right)\) và\(\,\left( {{C_2}} \right)\) tiếp xúc ngoài.
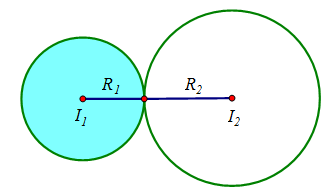
Khi đó: \({R_1} + {R_2} = {I_1}{I_2}\)\(\Leftrightarrow\sqrt m + \sqrt 2 = \sqrt {10} \)\( \Leftrightarrow m = {\left( {\sqrt {10} - \sqrt 2 } \right)^2}\)
Trường hợp 2: \(\,\left( {{C_1}} \right)\) nằm trong \(\,\left( {{C_2}} \right)\) và hai đường tròn tiếp xúc trong.
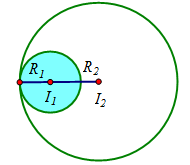
Khi đó: \({R_2} - {R_1} = {I_1}{I_2}\)\( \Leftrightarrow \sqrt m - \sqrt 2 = \sqrt {10} \) \( \Leftrightarrow m = {\left( {\sqrt {10} + \sqrt 2 } \right)^2}\)
Vậy \(m = {\left( {\sqrt {10} - \sqrt 2 } \right)^2}\) và \(m = {\left( {\sqrt {10} + \sqrt 2 } \right)^2}\) thỏa mãn yêu cầu bài toán.
Tìm tất cả các giá trị của $m$ để hệ sau có nghiệm $\left\{ \begin{array}{l}{3^{2x + \sqrt {x + 1} }} - {3^{2 + \sqrt {x + 1} }} + 2017x \le 2017\\{x^2} - \left( {m + 2} \right)x + 2m + 3 \ge 0\end{array} \right.$.
Điều kiện $x \ge - 1$.
Xét ${3^{2x + \sqrt {x + 1} }} - {3^{2 + \sqrt {x + 1} }} + 2017x \le 2017$$ \Leftrightarrow {3^{2x}}{.3^{\sqrt {x + 1} }} - {3^2}{.3^{\sqrt {x + 1} }} \le 2017 - 2017x$
$ \Leftrightarrow $$\left( {{9^x} - 9} \right){3^{\sqrt {x + 1} }} \le 2017\left( {1 - x} \right)$. Dễ thấy $x = 1$ là một nghiệm.
Nếu $x > 1$ thì $VT = \left( {{9^x} - 9} \right){3^{\sqrt {x + 1} }} > 0$, $VP = 2017\left( {1 - x} \right) < 0$
Suy ra $\left( {{9^x} - 9} \right){3^{\sqrt {x + 1} }} \le 2017\left( {1 - x} \right)$ vô nghiệm.
Nếu $ - 1 \le x < 1$ thì $VT = \left( {{9^x} - 9} \right){3^{\sqrt {x + 1} }} < 0$, $VP = 2017\left( {1 - x} \right) > 0$
Suy ra $\left( {{9^x} - 9} \right){3^{\sqrt {x + 1} }} \le 2017\left( {1 - x} \right)$ có nghiệm với $ - 1 \le x < 1$
Vậy bpt ${3^{2x + \sqrt {x + 1} }} - {3^{2 + \sqrt {x + 1} }} + 2017x \le 2017$ có nghiệm với $ - 1 \le x \le 1$
Bài toán trở thành tìm $m$ để bpt ${x^2} - \left( {m + 2} \right)x + 2m + 3 \ge 0$ có nghiệm $ - 1 \le x \le 1$
BPT \( \Leftrightarrow m\left( {x - 2} \right) \le {x^2} - 2x + 3\) \( \Leftrightarrow m \ge \dfrac{{{x^2} - 2x + 3}}{{x - 2}} = f\left( x \right)\) \(\left( * \right)\) (Do $ - 1 \le x \le 1$)
\(f'\left( x \right) = \dfrac{{{x^2} - 4x + 1}}{{{{\left( {x - 2} \right)}^2}}}\)
Xét \(f'\left( x \right) = 0 \Leftrightarrow x = 2 - \sqrt 3 \in \left[ { - 1;1} \right]\)
Để bpt \(\left( * \right)\) có nghiệm thì \(m \ge \mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 1;1} \right]} .\)
Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên \(\left[ { - 1;1} \right]\) ta có \(m \ge f\left( 1 \right) = f\left( { - 1} \right) = - 2\)
Vậy \(m \ge - 2\).
Cho phương trình 4 \({4^{ - |x - m|}} \cdot {\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}} \cdot {\log _{\frac{1}{2}}}(2|x - m| + 2) = 0\) với \(m\) là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là
3
3
3
Bước 1: Biến đổi phương trình để đưa về dạng xét hàm đặc trưng
Phương trình đã cho tương đương với phương trình
\({2^{ - 2}}|x - m| + 1 \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( - {2^{2x - {x^2}}} \cdot {\log _2}(2|x - m| + 2) = 0\) \( \Leftrightarrow {2^{ - 2}}|x - m| + 1 \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( = {2^{2x - {x^2}}} \cdot {\log _2}(2|x - m| + 2)\)
\( \Leftrightarrow {2^{{x^2} - 2x}} \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( = {2^2}|x - m| - 1 \cdot {\log _2}(2|x - m| + 2)\)
Bước 2: Xét hàm đặc trưng \(f(t) = {2^{t - 3}} \cdot {\log _2}t\) với \(t \ge 2\) rồi cô lập m, \(m = g\left( x \right)\)
Xét hàm số \(f(t) = {2^{t - 3}} \cdot {\log _2}t\) với \(t \ge 2\). Do \(t \ge 2\) suy ra \({\log _2}t \ge 1\).
Ta có: \({f^\prime }(t) = {2^{t - 3}} \cdot \dfrac{1}{{t.\ln 2}} + {2^{t - 3}} \cdot \ln 2 \cdot {\log _2}t > 0\) với \(t \ge 2\).
Do đó hàm số \(f(t)\) đồng biến trên \([2; + \infty )\)
\( \Rightarrow f\left( {{x^2} - 2x + 3} \right) = f(2|x - m| + 2)\)\( \Leftrightarrow {x^2} - 2x + 3 = 2|x - m| + 2\)\( \Leftrightarrow |x - m| = \dfrac{{{x^2}}}{2} - x + \dfrac{1}{2}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}}\\{m = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}}\end{array}(*)} \right.\)
Bước 3: Tìm tổng các giá trị m để phương trình có 3 nghiệm
Vẽ đồ thị các hàm số \(y = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}\) và \(y = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}\) trên cùng một hệ trục tọa độ.
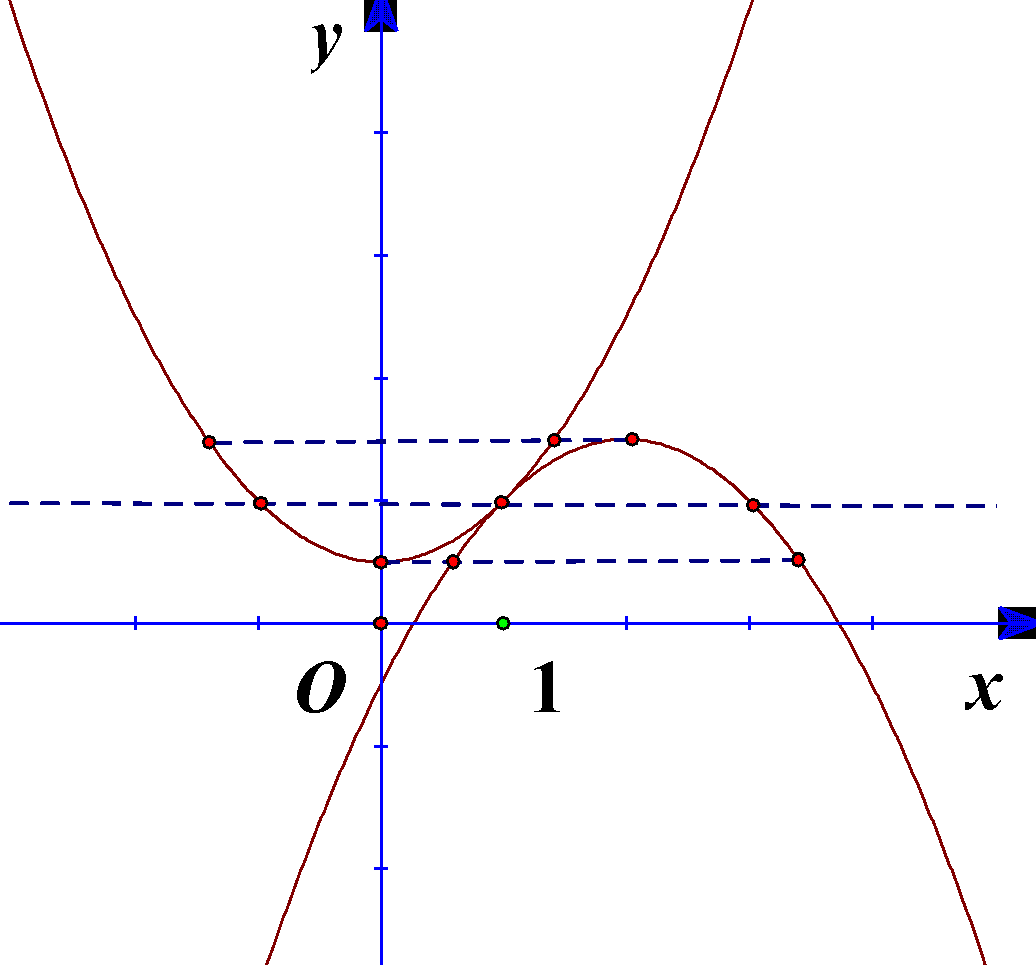
Đồ thị hai hàm số tiếp xúc với nhau tại điểm \((1;1)\). Điểm cực trị của đồ thị hàm số \(y = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}\) là \(\left( {0;\dfrac{1}{2}} \right)\), điểm cực trị của đồ thị hàm số \(y = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}\) là \(\left( {2;\dfrac{3}{2}} \right)\). Dựa vào đồ thị, để (*) có ba nghiệm phân biệt thì \(m \in \left\{ {\dfrac{1}{2};1;\dfrac{3}{2}} \right\}\). Tổng tất cả các giá trị của tham số \(m\) thỏa mãn là \(\dfrac{1}{2} + 1 + \dfrac{3}{2} = 3\).
