Bát diện đều có mấy đỉnh ?
Hình bát diện đều có \(6\) đỉnh.
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).
Ta có \(SA = a,{\rm{ }}{{\rm{S}}_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Suy ra thể tích \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
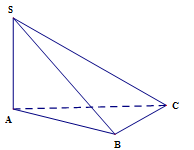
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C,\)\(AB = a\sqrt 5 ,\)\(AC = a.\) Cạnh bên \(SA = 3a\) và vuông góc với mặt phẳng đáy. Thể tích của khối chóp \(S.ABC\) bằng
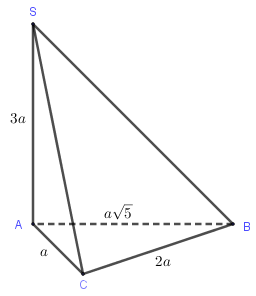
Vì \(\Delta ABC\) vuông nên áp dụng pitago.
\(CB = \sqrt {A{B^2} - A{C^2}} = \sqrt {5{a^2} - {a^2}} = 2a.\).
Diện tích đáy \({S_{\Delta ABC}} = \dfrac{1}{2}.a.2a = {a^2}\).
Thể tích khối chóp: \({V_{S.ABC}} = \dfrac{1}{3}.{S_{\Delta ABC}}.SA = \dfrac{1}{3}.{a^2}.3a = {a^3}.\)
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(2a\) và thể tích bằng \({a^3}\). Tính chiều cao \(h\) của hình chóp đã cho.
Do đáy là tam giác đều nên \({S_{\Delta ABC}} = \dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Mà \(V = \dfrac{1}{3}{S_{\Delta ABC}}.h \) \(\Rightarrow h = \dfrac{{3V}}{{{S_{\Delta ABC}}}} = \dfrac{{3{a^3}}}{{{a^2}\sqrt 3 }} = \sqrt 3 a\)
Cho tứ diện \(ABCD\) có thể tích bằng $12$ và \(G\) là trọng tâm tam giác \(BCD\). Tính thể tích \(V\) của khối chóp \(A.GBC\).

Tứ diện \(ABCD\) và khối chóp \(A.GBC\) có cùng đường cao là khoảng cách từ \(A\) đến mặt phẳng $\left( {BCD} \right)$. Do \(G\) là trọng tâm tam giác \(BCD\) nên ta có \({S_{\Delta BGC}} = {S_{\Delta BGD}} = {S_{\Delta CGD}}\)\( \Rightarrow {S_{\Delta BCD}} = 3{S_{\Delta BGC}}\)
Áp dụng công thức thể tích hình chóp ta có:
\(\left. \begin{array}{l}{V_{A.BCD}} = \dfrac{1}{3}h.{S_{\Delta BCD}}\\{V_{A.GBC}} = \dfrac{1}{3}h.{S_{\Delta GBC}}\end{array} \right\} \) \(\Rightarrow \dfrac{{{V_{A.BCD}}}}{{{V_{A.GBC}}}} = \dfrac{{\dfrac{1}{3}h.{S_{\Delta BCD}}}}{{\dfrac{1}{3}h.{S_{\Delta GBC}}}} = \dfrac{{{S_{\Delta BCD}}}}{{{S_{\Delta GBC}}}} = 3\)\( \Rightarrow {V_{A.GBC}} = \dfrac{1}{3}{V_{ABCD}} = \dfrac{1}{3}.12 = 4\).
Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).
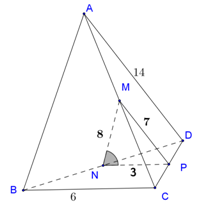
Gọi \(P\) là trung điểm của cạnh \(CD\), ta có \(\alpha = \widehat {\left( {MN,BC} \right)} = \widehat {\left( {MN,NP} \right)}\).
Trong tam giác \(MNP\), ta có \(\cos \widehat {MNP} = \dfrac{{M{N^2} + P{N^2} - M{P^2}}}{{2MN.NP}} = \dfrac{1}{2}\). Suy ra \(\widehat {MNP} = 60^\circ \).
Suy ra \(\sin \alpha = \dfrac{{\sqrt 3 }}{2}\).
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, \(SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Thể tích của khối chóp $S.ABCD$ bằng
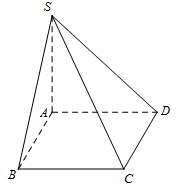
${V_{S.ABCD}} = \dfrac{1}{3}SA \cdot {S_{ABCD}} = \dfrac{1}{3} \cdot a\sqrt 6 \cdot {a^2} = \dfrac{{{a^3}\sqrt 6 }}{3}$.
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, \(SD = \dfrac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc $H$ của $S$ lên mặt $\left( {ABCD} \right)$ là trung điểm của đoạn $AB$. Tính chiều cao của khối chóp $H.SBD$ theo $a$.
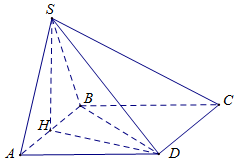
Ta có \(\Delta SHD\) vuông tại $H$$ \Rightarrow SH = \sqrt {S{D^2} - H{D^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt {17} }}{2}} \right)}^2} - \left( {{a^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} \right)} = a\sqrt 3 $.
\(V_{S.ABCD }= \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{{\sqrt 3 }}{3}{a^3}\) \( \Rightarrow \) ${V_{H.SBD}} = \dfrac{1}{2}{V_{A.SBD}} = \dfrac{1}{2}{V_{S.ABD}} = \dfrac{1}{4}{V_{S.ABCD}} = \dfrac{{\sqrt 3 }}{{12}}{a^3}$
Tam giác \(\Delta SHB\) vuông tại $H$$ \Rightarrow SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {3{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {13} }}{2}$
Tam giác \(\Delta SBD\) có $SB = \dfrac{{a\sqrt {13} }}{2};BD = a\sqrt 2 ;SD = \dfrac{{a\sqrt {17} }}{2}$ \( \Rightarrow \) \({S_{\Delta SBD}} = \dfrac{{5{a^2}}}{4}\)
\( \Rightarrow \)\(d\left( {H,\left( {SBD} \right)} \right) = \dfrac{{3{V_{S.HBD}}}}{{{S_{\Delta SBD}}}} = \dfrac{{a\sqrt 3 }}{5}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, $AB = a$, $\widehat {BAD} = 60^\circ $, $SO \bot \left( {ABCD} \right)$ và mặt phẳng $\left( {SCD} \right)$ tạo với mặt đáy một góc $60^\circ $. Tính thể tích khối chóp $S.ABCD$
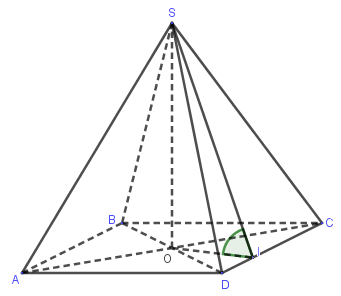
${S_{ABCD}} = 2{S_{ABD}} = AB.AD.\sin \widehat {BAD} = a.a.\sin 60^\circ = \dfrac{{{a^2}\sqrt 3 }}{2}$
Trong $\left( {ABCD} \right)$, dựng $OI \bot CD$.
Ta có $\left. \begin{array}{l}CD \bot OI\\CD \bot SO\end{array} \right\} \Rightarrow CD \bot \left( {SOI} \right) \Rightarrow CD \bot SI$
Do đó, $\left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SI,OI} \right) = \widehat {SIO} = 60^\circ $
Tam giác $OCI$ vuông tại $I$ nên
$\sin \widehat {OCI} = \dfrac{{OI}}{{OC}} \Leftrightarrow OI = OC.\sin \widehat {OCI} = \dfrac{{a\sqrt 3 }}{2}.\sin 30^\circ = \dfrac{{a\sqrt 3 }}{4}$
Tam giác $SOI$ vuông tại $O$ nên $\tan \widehat {SIO} = \dfrac{{SO}}{{OI}} \Rightarrow SO = OI.\tan \widehat {SIO} = \dfrac{{a\sqrt 3 }}{4}.\tan 60^\circ = \dfrac{{3a}}{4}$
Vậy ${V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{2}.\dfrac{{3a}}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}$
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(V\) là thể tích khối chóp \(S.ABCD\). Lấy điểm \(A'\) trên cạnh \(SA\)sao cho \(SA = 4SA'\). Mặt phẳng qua \(A'\) và song song với đáy của hình chóp cắt các cạnh \(SB\), \(SC\), \(SD\) lần lượt tại các điểm \(B'\), \(C'\), \(D'\). Thể tích khối chóp \(S.A'B'C'D'\)bằng:
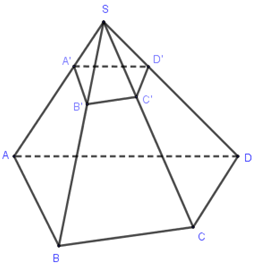
\(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}} = \dfrac{1}{{64}}\).
\(\dfrac{{{V_{S.A'D'C'}}}}{{{V_{S.ADC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SD'}}{{SD}}.\dfrac{{SC'}}{{SC}} = \dfrac{1}{{64}}\).
Suy ra \({V_{S.A'B'C'}} + {V_{S.A'D'C'}} = \dfrac{1}{{64}}\left( {{V_{S.ABC}} + {V_{S.ADC}}} \right)\).
hay \({V_{S.A'B'C'D'}} = \dfrac{1}{{64}}{V_{S.ABCD}} = \dfrac{V}{{64}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Nếu khối chóp có chiều cao bằng \(a\sqrt 3 \) và thể tích là \(3{a^3}\sqrt 3 \) thì cạnh đáy có độ dài là:
Gọi độ dài cạnh đáy là \(x\).
Có \({V_{S.ABCD}} = \dfrac{1}{3}{x^2}.a\sqrt 3 \Leftrightarrow 3{a^3}\sqrt 3 = \dfrac{1}{3}{x^2}.a\sqrt 3 \)\( \Leftrightarrow {x^2} = 9{a^2} \Leftrightarrow x = 3a.\)
Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là \(15{\rm{cm}}\) và \(5{\rm{cm}}\). Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho cây nến nằm khít trong hộp ( có đáy tiếp xúc như hình vẽ). Thể tích của chiếc hộp đó bằng.
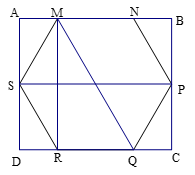
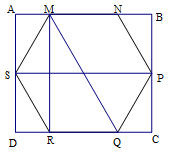
Ta có \(AB = SP = 2MN = 10cm\).
\(AD = MR = 2.\sqrt {{5^2} - {{\left( {\dfrac{5}{2}} \right)}^2}} = 5\sqrt 3 \)
\( \Rightarrow {S_{ABCD}} = AB.AD = 50\sqrt 3 \,\,c{m^2}\).
$V = {S_{ABCD}}.h = 50\sqrt 3 .15 = 750\sqrt 3 \,c{m^3}$.
Một khối chóp có đáy là đa giác $n$ cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?
Khối chóp có đáy là đa giác \(n\) cạnh thì có \(n + 1\) đỉnh và \(n + 1\) mặt, \(2n\) cạnh nên chỉ có A đúng.
Một hình chóp tứ giác đều có mấy mặt đối xứng:
Hình chóp tứ giác đều $S.ABCD$ có đáy là hình vuông, hình chiếu của đỉnh $S$ trên đáy trùng với tâm đáy.
Hình chóp $S.ABCD$ có các mặt đối xứng là $(SAC), (SBD), (SGI), (SHJ)$ với $G, H, I, J$ lần lượt là trung điểm $AB, BC, CD, DA$
Cho lăng trụ tam giác \(ABC.A'B'C'\) có đáy \(ABC\) là đều cạnh \(AB = 2a\sqrt 2 \). Biết \(AC' = 8a\) và tạo với mặt đáy một góc \({45^0}\). Thể tích khối đa diện \(ABCC'B'\) bằng
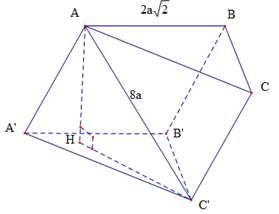
Gọi \(H\) là hình chiếu của \(A\) lên \(mp\left( {A'B'C'} \right)\).
\( \Rightarrow \widehat {HC'A} = {45^0}\).
\( \Rightarrow \Delta AHC'\) vuông cân tại $H.$
\( \Rightarrow AH = AC'.\sin 45^0=AC'.\dfrac{{\sqrt 2}}{{2}} = 4a\sqrt 2 .\)
Diện tích tam giác $ABC$ là: $S_{ABC}=\dfrac{(2a\sqrt{2})^2\sqrt{3}}{4}$
NX: \({V_{A.BCC'B'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}AH.{S_{ABC}} = \dfrac{2}{3}.4a\sqrt 2 .\dfrac{{{{\left( {2a\sqrt 2 } \right)}^2}.\sqrt 3 }}{4} = \dfrac{{16{a^3}\sqrt 6 }}{3}.\)
Cho hình lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(V\). Các điểm \(M\), \(N\), \(P\) lần lượt thuộc các cạnh $AA'$, $BB'$, $CC'$ sao cho $\dfrac{{AM}}{{AA'}} = \dfrac{1}{2}$, $\dfrac{{BN}}{{BB'}} = \dfrac{{CP}}{{CC'}} = \dfrac{2}{3}$. Thể tích khối đa diện \(ABC.MNP\) bằng
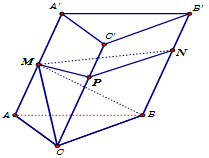
Có ${V_{A'.B'C'CB}} = \dfrac{2}{3}V = {V_{M.B'C'CB}}$
Đặt: ${V_1} = {V_{M.NPCB}} = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{NPCB}}$
$ = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).\dfrac{2}{3}{S_{CC'B'B}}$ $ = \dfrac{2}{3}.\dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{CC'B'B}} $ $= \dfrac{2}{3}{V_{M.CC'B'B}} = \dfrac{2}{3}.\dfrac{2}{3}.V = \dfrac{4}{9}V$
$\begin{array}{l}{V_2} = {V_{M.ABC}} = \dfrac{1}{3}d\left( {M,\left( {ABC} \right)} \right).{S_{ABC}}\\ = \dfrac{1}{3}.\dfrac{1}{2}d\left( {A',\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{6}V\end{array}$
Vậy \({V_{ABC.MNP}} = {V_1} + {V_2} = \dfrac{4}{9}V + \dfrac{1}{6}V = \dfrac{{11}}{{18}}V\)
Hình đa diện nào dưới đây không có tâm đối xứng ?
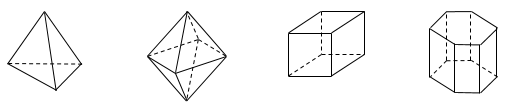
Dễ dàng thấy bát diện đều, hình lập phương và lăng trục lục giác đều có tâm đối xứng. Còn tứ diện đều không có tâm đối xứng.
Thật vậy, giả sử tứ diện đều ABCD có tâm đối xứng O. Nhận thấy các đỉnh A,B,C,D không thể là tâm đối xứng của tứ diện ABCD, nên ảnh của A qua đối xứng tâm O là một trong ba đỉnh còn lại, nếu $D_O(A)=B$ thì O là trung điểm của AB, nhưng trung điểm của AB cũng không thể là tâm đối xứng của ABCD
Cho tứ diện đều \(ABCD\) có cạnh bằng $3.$ Gọi \(M,\,N\) lần lượt là trung điểm các cạnh \(AD,\,BD.\) Lấy điểm không đổi \(P\) trên cạnh \(AB\) (khác \(A,\,B\)). Thể tích khối chóp \(P.MNC\) bằng
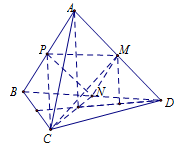
Do \(AB\parallel \left( {CMN} \right)\) nên \(d\left( {P,\,\left( {CMN} \right)} \right) = d\left( {A,\,\left( {CMN} \right)} \right) = d\left( {D,\,\left( {CMN} \right)} \right)\).
Vậy \({V_{PCMN}} = {V_{DMNC}} = {V_{MCND}} = \dfrac{1}{4}{V_{ABCD}}\).
(Do diện tích đáy và chiều cao đều bằng một nửa).
Mặt khác \({V_{ABCD}} = \dfrac{1}{3}\dfrac{{{a^2}\sqrt 3 }}{4}.\sqrt {{a^2} - {{\left( {\dfrac{a}{{\sqrt 3 }}} \right)}^2}} = \dfrac{{{a^3}\sqrt 2 }}{{12}} = \dfrac{{27\sqrt 2 }}{{12}}\) nên \({V_{P.MNC}} = \dfrac{1}{4}.\dfrac{{27\sqrt 2 }}{{12}} = \dfrac{{9\sqrt 2 }}{{16}}\).
Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều

Bát diện đều có $8$ mặt là các tam giác đều.
Nhị thập diện đều có $20$ mặt là các tam giác đều.
Tứ diện đều có $4$ mặt là các tam giác đều.
Thập nhị diện đều có $12$ mặt là các ngũ giác đều.
Có tất cả bao nhiêu khối đa diện đều?
Có $5$ và chỉ $5$ khối đa diện đều: Khối tứ diện đều, khối lập phương, khối bát diện đều, khối $12$ mặt đều, khối $20$ mặt đều.

