Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, \(SD = \dfrac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc $H$ của $S$ lên mặt $\left( {ABCD} \right)$ là trung điểm của đoạn $AB$. Tính chiều cao của khối chóp $H.SBD$ theo $a$.
Trả lời bởi giáo viên
Đáp án đúng: a
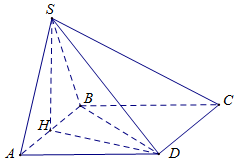
Ta có \(\Delta SHD\) vuông tại $H$$ \Rightarrow SH = \sqrt {S{D^2} - H{D^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt {17} }}{2}} \right)}^2} - \left( {{a^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} \right)} = a\sqrt 3 $.
\(V_{S.ABCD }= \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{{\sqrt 3 }}{3}{a^3}\) \( \Rightarrow \) ${V_{H.SBD}} = \dfrac{1}{2}{V_{A.SBD}} = \dfrac{1}{2}{V_{S.ABD}} = \dfrac{1}{4}{V_{S.ABCD}} = \dfrac{{\sqrt 3 }}{{12}}{a^3}$
Tam giác \(\Delta SHB\) vuông tại $H$$ \Rightarrow SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {3{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {13} }}{2}$
Tam giác \(\Delta SBD\) có $SB = \dfrac{{a\sqrt {13} }}{2};BD = a\sqrt 2 ;SD = \dfrac{{a\sqrt {17} }}{2}$ \( \Rightarrow \) \({S_{\Delta SBD}} = \dfrac{{5{a^2}}}{4}\)
\( \Rightarrow \)\(d\left( {H,\left( {SBD} \right)} \right) = \dfrac{{3{V_{S.HBD}}}}{{{S_{\Delta SBD}}}} = \dfrac{{a\sqrt 3 }}{5}.\)
Hướng dẫn giải:
- Tính thể tích \(V\) của khối chóp \(H.SBD\)
- Tính chiều cao của khối chóp \(H.SBD\) (hay khoảng cách từ \(H\) đến \(mp\left( {SBD} \right)\)) theo công thức \(h = \dfrac{{3V}}{S}\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
