Khái niệm về khối đa diện (sự bằng nhau của các khối đa diện)

Phép đối xứng qua mặt phẳng \(\left( P \right)\) là phép biến hình biến mỗi điểm thuộc \(\left( P \right)\) thành chính nó nên \(A \equiv A'\).

Phép đối xứng qua mặt phẳng bảo toàn khoảng cách giữa hai điểm nên A, D đúng.

Phép đối xứng qua mặt phẳng biến một đường thẳng song song với mặt phẳng thành đường thẳng song song và cách đều mặt phẳng so với đường thẳng ban đầu nên B đúng và C sai.

Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến \(A\) thành \(A'\) nên \(A'A \bot \left( P \right)\).

Mặt phẳng \(\left( P \right)\) là mặt phẳng trung trực của \(AB\) thì \(A,B\) đối xứng nhau qua \(\left( P \right)\).

Hình chóp tam giác đều có mặt phẳng đối xứng (các mặt phẳng đi qua cạnh bên hình chóp và trung điểm cạnh đối diện)

Do đó có hai hình có mặt phẳng đối xứng là tứ diện đều và hình chóp tam giác đều.

Phép dời hình bảo toàn khoảng cách giữa hai điểm.

Phép dời hình biến mặt phẳng thành mặt phẳng.

Hai hình tứ diện có tất cả các cạnh bằng nhau và bằng \(a\) thì chúng bằng nhau.

Hai hình chóp đều có chung đáy là các tam giác đều nên muốn bằng nhau chỉ cần các cạnh bên bằng nhau. Do đó khoảng cách từ hai đỉnh đến mặt đáy cũng bằng nhau.

Vậy hai đỉnh đối xứng nhau qua mặt đáy.

Phép đối xứng qua mặt phẳng là phép dời hình nên nếu nó biến hình lập phương \(ABCD.A'B'C'D'\) thành hình lập phương \(MNPQ.M'N'P'Q'\) thì hai hình này bằng nhau hay chúng có các cạnh bằng nhau.

Vậy \(AB = M'N'\).

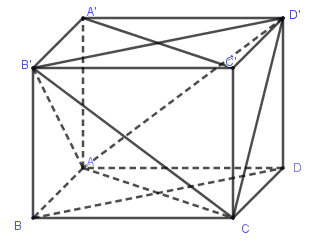
Hai hình chóp \(B'.ABC\) và \(D'.ADC\) bằng nhau vì tồn tại phép đối xứng qua mặt phẳng \(\left( {ACC'A'} \right)\) biến \(B'.ABC\) thành \(D'.ADC\).

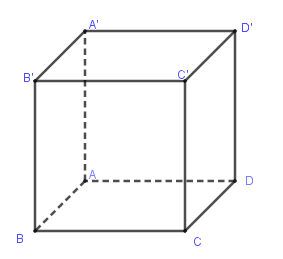
Dễ thấy, các phép tịnh tiến theo mỗi véc tơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\) nên B, C đúng, D sai.

Phép đối xứng qua tâm \(O\) của hình lập phương biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\) nên A đúng.

Phép đối xứng qua mặt phẳng \(\left( P \right)\) là phép biến hình biến mỗi điểm thuộc \(\left( P \right)\) thành chính nó.

Phép đối xứng qua mặt phẳng bảo toàn khoảng cách giữa 2 điểm bất kì nên \(M'N' = MN\).

Phép đối xứng qua mặt phẳng \(\left( P \right)\) là phép biến hình biến mỗi điểm thuộc \(\left( P \right)\) thành chính nó và biến mỗi điểm \(M\) không thuộc \(\left( P \right)\) thành điểm \(M'\) sao cho \(\left( P \right)\) là mặt phẳng trung trực của \(MM'\).

Do đó \(MM' \bot \left( P \right)\).

Vì \(\left( P \right)\) là mặt phẳng trung trực của \(BB'\) nên mọi điểm thuộc \(\left( P \right)\) sẽ cách đều \(B,B' \Rightarrow AB = AB'\).

Do đó \(\Delta ABB'\) cân tại \(A\).

Hình chóp tam giác đều có mặt phẳng đối xứng (các mặt phẳng đi qua cạnh bên hình chóp và trung điểm cạnh đối diện)

Tứ diện đều có mặt phẳng đối xứng là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện. Vì tứ diện đều có 6 cạnh nên có 6 mặt phẳng đối xứng.

Mọi mặt phẳng đi qua tâm của mặt cầu đều là mặt phẳng đối xứng của mặt cầu.

Vậy có vô số mặt phẳng đối xứng.

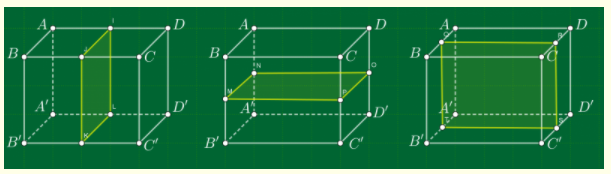
Hình hộp chữ nhật có \(3\) mặt phẳng đối xứng, đó là mặt phẳng đi qua trung điểm các cạnh đối diện.