Cho các hình sau: hình chóp tam giác đều, hình hộp đứng, hình lăng trụ tam giác đều, hình chóp tứ giác có đáy là hình thoi, hình hộp có đáy là hình thoi. Số hình có mặt phẳng đối xứng là:
Các hình có mặt phẳng đối xứng là:
+ Hình chóp tam giác đều có \(3\) mặt phẳng đối xứng.
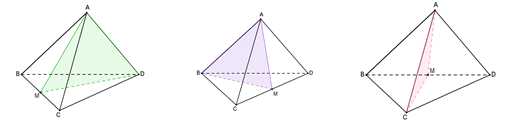
+ Hình hộp đứng có \(1\) mặt phẳng đối xứng.
+ Hình lăng trụ tam giác đều có \(4\) mặt phẳng đối xứng.
+ Hình hộp có đáy là hình thoi không có mặt phẳng đối xứng.
+ Hình chóp tứ giác có đáy là hình thoi không có mặt phẳng đối xứng.
Vậy có \(3\) hình có mặt phẳng đối xứng.
Số mặt phẳng đối xứng của hình bát diện đều là:
Hình bát diện đều có \(9\) mặt phẳng đối xứng.

Phép dời hình biến đoạn thẳng thành:
Phép dời hình bảo toàn khoảng cách giữa \(2\) điểm nên đoạn thẳng sẽ có độ dài bằng đoạn thẳng đã cho.
Phép dời hình biến đường thẳng thành:
Phép dời hình biến đường thẳng thành đường thẳng.
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
Hai tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.
Cho hai hình chóp tam giác đều cạnh đáy bằng \(a\). Cần bổ sung thêm điều kiện gì để hai hình chóp đó bằng nhau?
Vì cả hai hình chóp tam giác đều có cách cạnh đáy bằng nhau và bằng \(a\) nên chúng chỉ cần có các cạnh bên bằng nhau là đủ.
Chọn mệnh đề đúng:
- Nếu có một phép dời hình biến hình \(H'\) thành \(H\) thì hai hình bằng nhau và phép tịnh tiến cũng là một phép dời hình nên B đúng.
- Các đáp án A, C, D đều sai vì hai hình bằng nhau có thể là hợp thành của một số phép dời hình chứ không nhất thiết là chỉ một phép dời hình.
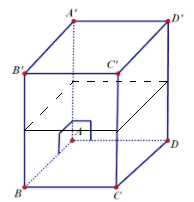
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Hình nào dưới đây bằng hình chóp \(A'.ABCD\)?
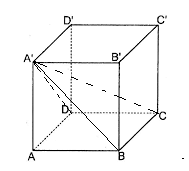
Xét hai hình chóp \(A'.ABCD\) và \(C'.ABCD\) có:
Tồn tại phép đối xứng qua mặt phẳng \(\left( {B{\rm{D}}D'B'} \right)\) biến hình chóp \(A'.ABCD\) thành \(C'.ABCD\) nên chúng bằng nhau.
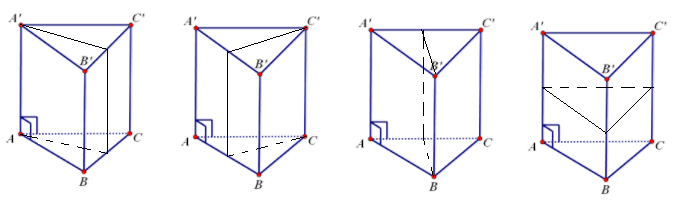
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Hình nào dưới đây bằng hình lăng trụ \(ABC.A'B'C'\)?
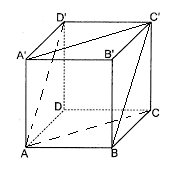
Ta thấy hai lăng trụ đứng \(ABC.A'B'C'\) và \(AA'D'.BB'C'\) có một phép đối xứng qua mặt phẳng \(\left( {AB'C'D} \right)\) nên hai lăng trụ này bằng nhau.
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng như hình vẽ dưới:
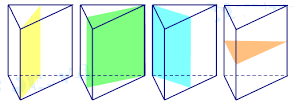
Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
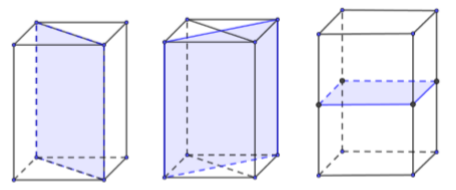
Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có 3 mặt phẳng đối xứng.
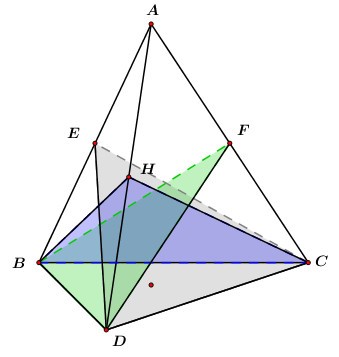
Cho tứ diện \(ABCD\) có ba mặt \(ABC,\,\,ACD,\,\,ADB\) là ba tam giác bằng nhau và cân tại định \(A.\) Số mặt phẳng đối xứng của tứ diện đó là:
Ta có: Ba mặt \(ABC,\,\,ACD,\,\,ADB\) là ba tam giác bằng nhau và cân tại định \(A\)
\( \Rightarrow \left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\)
TH1: Ta có: \(\left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\) và các cạnh bên không bằng các cạnh đáy
Khi đó ta có các mặt phẳng đối xứng là: \(\left( {ABN} \right),\,\,\left( {ACM} \right),\,\,\left( {ADP} \right)\) với \(M,\,\,N,\,\,P\) lần lượt là trung điểm của các cạnh \(BD,\,\,DC,\,\,BC.\)
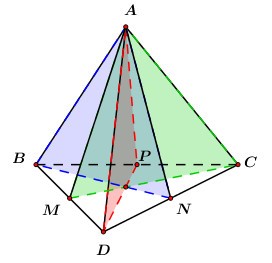
TH2: Ta có: \(\left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\) và các cạnh bên bằng các cạnh đáy
Khi đó ta có các mặt đối xứng như TH1 và thêm các mặt phẳng \(\left( {EDC} \right),\,\,\left( {FBD} \right),\,\,\left( {HBC} \right)\) với \(E,\,\,F,\,\,H\) lần lượt là trung điểm của các cạnh \(AB,\,\,AC,\,\,AD.\)