Cho hình phẳng \(\left( H \right)\) giới hạn bởi parabol \(y = a{x^2} + 1\,\,\,\left( {a > 0} \right)\), trục tung và đường thẳng \(x = 1\). Quay \(\left( H \right)\) quanh trục Ox được một khối tròn xoay có thể tích bằng \(\dfrac{{28}}{{15}}\pi \). Mệnh đề nào dưới đây đúng?
\(\begin{array}{l}V = \dfrac{1}{2}.\left( {\int\limits_0^1 {\dfrac{{\sqrt 3 .4{{\left( {1 - x} \right)}^2}}}{4} + \int\limits_{ - 1}^0 {\dfrac{{\sqrt 3 .4{{\left( {x + 1} \right)}^2}}}{4}} } } \right)\\ = \dfrac{{\sqrt 3 }}{2}.\left( {\dfrac{1}{3} + \dfrac{1}{3}} \right) = \dfrac{\sqrt 3 }{3} \end{array}\)
Vậy \(0 < a < 2\)
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {\dfrac{x}{{4 - {x^2}}}} \), trục Ox và đường thẳng \(x = 1\). Khối tròn xoay sinh ra khi cho \(\left( H \right)\) quay quanh trục Ox có thể tích bằng
ĐKXĐ: \(\left\{ \begin{array}{l}\dfrac{x}{{4 - {x^2}}} \ge 0\\4 - {x^2} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < - 2\\0 \le x < 2\end{array} \right.\)
Hoành độ giao điểm của đồ thị hàm số \(y = \sqrt {\dfrac{x}{{4 - {x^2}}}} \) và trục hoành là \(\sqrt {\dfrac{x}{{4 - {x^2}}}} = 0 \Leftrightarrow x = 0\,\,\left( {tm} \right)\)
Thể tích khối tròn xoay khi quay hình \(\left( H \right)\) quanh trục Ox là \(V = \pi \int\limits_0^1 {\dfrac{x}{{4 - {x^2}}}dx} = \dfrac{\pi }{2}\ln \dfrac{4}{3}.\)
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
Ta có \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\Leftrightarrow {{\left( y-3 \right)}^{2}}=4-{{x}^{2}}\Leftrightarrow \left[\begin{align} & y=f\left( x \right)=\sqrt{4-{{x}^{2}}}+3 \\ & y=g\left( x \right)=-\,\sqrt{4-{{x}^{2}}}+3 \\\end{align} \right.\)
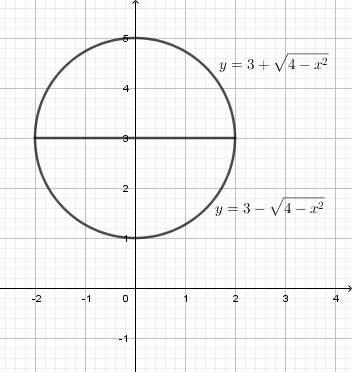
Vậy thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{-\,2}^{2}{{{f}^{2}}\left( x \right)\,\text{d}x}-\pi \int\limits_{-\,2}^{2}{{{g}^{2}}\left( x \right)\,\text{d}x}\)
\(\begin{align} & =\pi \int\limits_{-\,2}^{2}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\,\text{d}x} \\ & =\pi \int\limits_{-\,2}^{2}{\left( {{\left( \sqrt{4-{{x}^{2}}}+3 \right)}^{2}}-{{\left( 3-\sqrt{4-{{x}^{2}}} \right)}^{2}} \right)\,\text{d}x} \\ & =\pi \,\int\limits_{-\,2}^{2}{12\sqrt{4-{{x}^{2}}}\,\text{d}x}=24{{\pi }^{2}}. \\\end{align}\)
Vậy thể tích cần tính là \(V=24{{\pi }^{2}}.\)
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y = \sqrt {6 - {x^2}} \) \(\left( -\,\sqrt{6}\le x\le \sqrt{6} \right)\) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay sinh bởi khi quay hình phẳng \(D\) quanh trục \(Ox\).
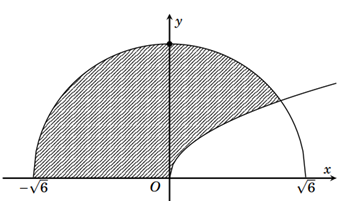
Cung tròn khi quay quanh \(Ox\) tạo thành một khối cầu có thể tích \(V=\frac{4}{3}\pi {{\left( \sqrt{6} \right)}^{3}}=8\pi \sqrt{6}\).
Thể tích nửa khối cầu là \({{V}_{1}}=4\pi \sqrt{6}\). Xét phương trình:
\(\sqrt x = \sqrt {6 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
{x^2} + x - 6 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
\left[ \begin{array}{l}
x = 2\\
x = - 3
\end{array} \right.
\end{array} \right. \Leftrightarrow x = 2.\)
Thể tích khối tròn xoay có được khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị các hàm số \(y=\sqrt{x}\), cung tròn có phương trình \(y=\sqrt{6-{{x}^{2}}}\), và hai đường thẳng \(x=0,\,\,x=2\) quanh \(Ox\) là:
\({{V}_{2}}=\pi \int\limits_{0}^{2}{\left( 6-{{x}^{2}}-x \right)\text{d}x}=\left. \pi \left( 6x-\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2} \right) \right|_{0}^{2}=\frac{22\pi }{3}.\)
Vậy thể tích vật thể tròn xoay cần tìm là \(V={{V}_{1}}+{{V}_{2}}=4\pi \sqrt{6}+\frac{22\pi }{3}\).
Trong mặt phẳng tọa độ Oxy, gọi \(\left( {{H_1}} \right)\) là hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2}}}{4};\,\,y = - \frac{{{x^2}}}{4};\,\,x = - 4;\,\,x = 4\) và \(\left( {{H_2}} \right)\) là hình gồm tất cả các điểm \(\left( {x;y} \right)\) thỏa \({x^2} + {y^2} \le 16;\,\,{x^2} + {\left( {y - 2} \right)^2} \ge 4;\,\,{x^2} + {\left( {y + 2} \right)^2} \ge 4\)
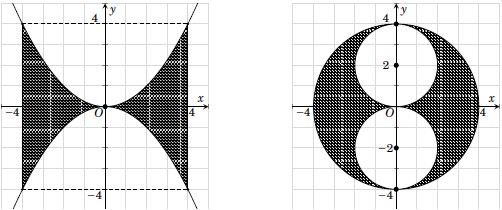
Cho \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\) quanh quanh trục Oy ta được các vật thể có thể tích là \({V_1},\,\,{V_2}\). Đẳng thức nào sau đây đúng ?
\({V_1}\) là hiệu thể tích khối trụ có bán kính đáy bằng $4$, chiều cao bằng $8$ với hai lần thể tích của vật thể tròn xoay tạo thành khi vật thể bị giới hạn bởi các đường \(x = 2\sqrt y ;\,\,x = 0;\,\,y = 0;\,\,x = 4\) quay quanh trục $Oy$.
\( \Rightarrow {V_1} = \pi {.4^2}.8 - 2\pi \int\limits_0^4 {4ydy} = 64\pi \)
\({V_2}\) là hiệu thể tích khối cầu có bán kính bằng $4$ với $2$ lần thể tích khối cầu có bán kính bằng $2$.
\( \Rightarrow {V_2} = \dfrac{4}{3}\pi \left( {{4^3} - {{2.2}^3}} \right) = 64\pi \)
Vậy \({V_1} = {V_2}\).
Cho nửa đường tròn đường kính \(AB=4\sqrt{5}\). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
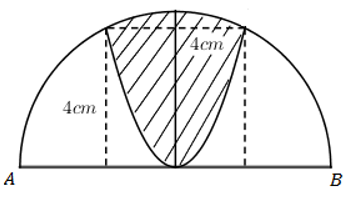
Gắn hệ trục tọa độ Oxy như hình vẽ:
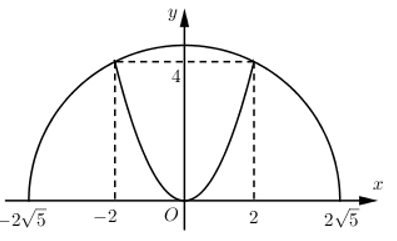
Ta có:
Đường tròn tâm \(O(0;0)\) bán kính $R = 2\sqrt 5 $ có phương trình: \({{x}^{2}}+{{y}^{2}}=20\Rightarrow y=\sqrt{20-{{x}^{2}}}\)
Parabol $y = a{x^2} + bx + c$ có đỉnh \(O(0;0)\) và đi qua điểm \((2;4)\) nên:
$\left\{ \begin{array}{l}
- \dfrac{b}{{2a}} = 0\\
a{.0^2} + b.0 + c = 0\\
a{.2^2} + b.2 + c = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b = 0\\
c = 0\\
a = 1
\end{array} \right.$
Vậy phương trình parabol: \(y={{x}^{2}}\)
Thể tích khối cầu \(V=\dfrac{4}{3}\pi {{\left( 2\sqrt{5} \right)}^{3}}=\dfrac{160\sqrt{5}}{3}\pi \)
Thể tích khi quay phần tô đậm quanh trục $Ox$ là: \(V'=\pi \int\limits_{-2}^{2}{\left( 20-{{x}^{2}}-{{x}^{4}} \right)dx}=\dfrac{928}{15}\pi \)
\(\Rightarrow \) Thể tích cần tính \({{V}_{1}}=V-V'=\dfrac{160\sqrt{5}}{3}\pi -\dfrac{928}{15}\pi =\dfrac{\pi }{15}\left( 800\sqrt{5}-928 \right)\)
Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\) và các đường thẳng \(y=0;\,\,x=1;\,\,x=4\). Tính thể tích V của khối tròn xoay sinh ra khi cho hình (H) quanh xung quanh trục Ox.
\(V = \pi \int\limits_1^4 {\frac{{dx}}{{{x^2}}}} = \pi \left( {\left. { - \frac{1}{x}} \right|_1^4} \right) = \pi \left( { - \frac{1}{4} + 1} \right) = \frac{{3\pi }}{4}\)
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y={{x}^{2}}\) và đường thẳng \(y=2x\). Tính thể tích $V$ của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục hoành.
Phương trình hoành độ giao điểm : \({{x}^{2}}=2x\Leftrightarrow \left[ \begin{align} x=0 \\ x=2 \\ \end{align} \right.\)
Thể tích cần tìm : \(V=~\pi \int_{0}^{2}{\left| {{\left( {{x}^{2}} \right)}^{2}}-{{\left( 2x \right)}^{2}} \right|dx}=\pi \int_{0}^{2}{\left| {{x}^{4}}-4{{x}^{2}} \right|dx}=\left| \pi \int_{0}^{2}{\left( {{x}^{4}}-4{{x}^{2}} \right)dx} \right|=\left| \pi \left. \left( \frac{1}{5}{{x}^{5}}-\frac{4}{3}{{x}^{3}} \right) \right|_{0}^{2} \right|=\left| \pi \left( \frac{32}{5}-\frac{32}{3} \right) \right|=\frac{64\pi }{15}\)
Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = - 1\) và \(x = 1\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) có hoành độ \(x\left( { - 1 \le x \le 1} \right)\) là một tam giác vuông cân với cạnh huyền bằng \(\sqrt {1 - {x^4}} \).
Diện tích tam giác vuông cân có cạnh huyền bằng \(\sqrt {1 - {x^4}} \) là \(S\left( x \right) = \dfrac{1}{2}{\left( {\dfrac{{\sqrt {1 - {x^4}} }}{{\sqrt 2 }}} \right)^2} = \dfrac{{1 - {x^4}}}{4}\).
Thể tích cần tìm là: \(V = \;\int_{ - 1}^1 {S\left( x \right)dx} = \dfrac{1}{4}\int_{ - 1}^1 {\left( {1 - {x^4}} \right)dx} = \left. {\dfrac{1}{4}\left( {x - \dfrac{1}{5}{x^5}} \right)} \right|_{ - 1}^1 = \dfrac{1}{4}\left( {\dfrac{4}{5} + \dfrac{4}{5}} \right) = \dfrac{2}{5}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm \(A\left( 2;4 \right),\) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng \(\left( H \right)\) khi quay xung quanh trục \(Ox.\)
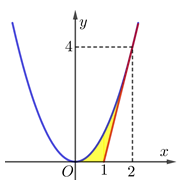
Vì \(\left( P \right)\) đi qua ba điểm \(O\left( 0;0 \right),\,\,A\left( 2;4 \right)\)
\(\Rightarrow \,\,\) Phương trình parabol là \(\left( P \right):y={{x}^{2}}.\) Tiếp tuyến của \(\left( P \right)\) tại điểm \(A\left( 2;4 \right)\) có phương trình là \(\left( d \right):y=4x-4.\)
Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm phương trình: \({{x}^{2}}=4x-4\Leftrightarrow x=2.\)
Thể tích khối tròn xoay khi quay hình phẳng \(\left( {{H}_{1}} \right)\) giới hạn bởi \(\left( P \right),\,\,y=0,\,\,x=0,\,\,x=2\) là \({{V}_{1}}=\pi \int\limits_{0}^{2}{{{f}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{0}^{2}{{{x}^{4}}\,\text{d}x}=\left. \frac{\pi {{x}^{5}}}{5} \right|_{0}^{2}=\frac{32\pi }{5}.\)
Thể tích khối tròn xoay khi quay hình phẳng \(\left( {{H}_{2}} \right)\) giới hạn bởi \(\left( d \right),\,\,y=0,\,\,x=1,\,\,x=2\) là \({{V}_{2}}=\pi \int\limits_{1}^{2}{{{g}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{1}^{2}{{{\left( 4x-4 \right)}^{2}}\,\text{d}x=}\pi \int\limits_{1}^{2}{16{{\left( x-1 \right)}^{2}}\,\text{d}x=}\left. \frac{16\pi {{\left( x-1 \right)}^{3}}}{3} \right|_{1}^{2}=\frac{16\pi }{3}.\)
Vậy thể tích khối tròn xoay cần tính là \(V={{V}_{1}}-{{V}_{2}}=\frac{32\pi }{5}-\frac{16\pi }{3}=\frac{16\pi }{15}.\)
Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm \(y=\tan x\), trục \(Ox\), đường thẳng \(x=0\), đường thẳng \(x=\frac{\pi }{3}\) quanh trục \(Ox\) là
Thể tích của vật tròn xoay là
\(V=\pi \int\limits_{0}^{\frac{\pi }{3}}{{{\tan }^{2}}x\text{d}x}\)\(=\pi \int\limits_{0}^{\frac{\pi }{3}}{\left( \frac{1}{{{\cos }^{2}}x}-1 \right)\text{d}x}\)\(=\pi \left. \left( \tan x-x \right) \right|_{0}^{\frac{\pi }{3}}\)\(=\pi \left( \tan \frac{\pi }{3}-\frac{\pi }{3} \right)\)\(=\pi \sqrt{3}-\frac{{{\pi }^{2}}}{3}\).
Thể tích vật thể nằm giữa hai mặt phẳng \(x=0\) và \(x=2\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( 0\le x\le 2 \right)\) là một nửa đường tròn đường kính \(\sqrt{5}{{x}^{2}}\) bằng :
Diện tích nửa hình tròn đường kính \(\sqrt{5}{{x}^{2}}\) là \(S\left( x \right)=\frac{1}{2}.\pi {{\left( \frac{\sqrt{5}{{x}^{2}}}{2} \right)}^{2}}=\frac{5\pi {{x}^{4}}}{8}\).
Vậy \(V=\int\limits_{0}^{2}{S\left( x \right)dx}=\int\limits_{0}^{2}{\frac{5\pi {{x}^{4}}}{8}dx}=\frac{5\pi }{8}\left. \frac{{{x}^{5}}}{5} \right|_{0}^{2}=4\pi \).
Viết công thức tính thể tích $V$ của phần vật thể nằm giữa hai mặt phẳng $x = 0$ và $x = \ln 4$, biết khi cắt vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ $x$ \(\left( 0\le x\le \ln 4 \right)\) , ta được thiết diện là một hình vuông có độ dài cạnh là \(\sqrt{x.{{e}^{x}}}\)
Diện tích thiết diện là \(S=x.{{e}^{x}}\)
Như vậy theo trên ta có thể tích \(V=\int\limits_{0}^{\ln 4}{x{{e}^{x}}dx}\)
Cho vật thể có mặt đáy là hình tròn bán kính bằng $1$ (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ \(\left( -1\le x\le 1 \right)\) thì thiết diện là một tam giác đều. Tính thể tích $V$ của vật thể đó.
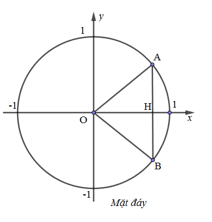
Ở mặt đáy, tam giác $OHB$ vuông tại $H$ \(\Rightarrow HB=\sqrt{O{{B}^{2}}-O{{H}^{2}}}=\sqrt{1-{{x}^{2}}}\)
\(\Rightarrow AB=2\sqrt{1-{{x}^{2}}}\)
Diện tích của mặt cắt khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ \(\left( -1\le x\le 1 \right)\)là:
\(S(x)=\frac{A{{B}^{2}}\sqrt{3}}{4}=\frac{{{\left( 2\sqrt{1-{{x}^{2}}} \right)}^{2}}.\sqrt{3}}{4}=\sqrt{3}(1-{{x}^{2}})\)
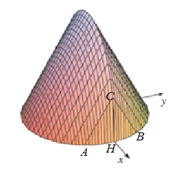
Thể tích cần tìm : \(V=\int\limits_{-1}^{1}{S(x)dx}=\int\limits_{-1}^{1}{\sqrt{3}(1-{{x}^{2}})dx}=\sqrt{3}\left. \left( x-\frac{1}{3}{{x}^{3}} \right) \right|_{-1}^{1}=\sqrt{3}.\frac{4}{3}=\frac{4\sqrt{3}}{3}\)
Viết công thức tính thể tich $V$ của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với $Ox$ tại các điểm \(x=a,x=b\,\,\left( a<b \right)\), có diện tích thiết diện bị cắt bởi hai mặt phẳng vuông với trục $Ox$ tại điểm có hoành độ \(x\,\,\left( a\le x\le b \right)\) là \(S\left( x \right)\).
Tính thể tích của vật thể giới hạn bởi các mặt phẳng \(x = a,x = b\) biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục $Ox$ là \(S = S\left( x \right)\).
Công thức tính: \(V = \int\limits_a^b {S\left( x \right)dx} \).
Trong không gian $Oxyz$, cho vật thể được giới hạn bởi 2 mặt phẳng \((P),\,\,(Q)\) vuông góc với $Ox$ lần lượt tại \(x = a,\,\,x = b,\,\,(a < b)\). Một mặt phẳng tùy ý vuông góc với $Ox$ tại điểm có hoành độ $x$, \((a \le x \le b)\) cắt vật thể theo thiết diện có diện tích là \(S(x)\), với \(y = S(x)\) là hàm số liên tục trên \(\left[ {a;b} \right]\). Thể tích $V$ của vật thế đó được tính theo công thức:
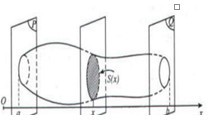
Thể tích $V$ của vật thế đó được tính theo công thức: \(V = \int\limits_a^b {S(x)dx} \).
Đề minh họa ĐGNL HN 2021
Cho (H) là hình phẳng giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) Thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox.
ĐKXĐ: \(x \ge 0.\)
Xét phương trình hoành độ giao điểm
\(\begin{array}{l}\sqrt x = {x^2} \Leftrightarrow \sqrt x \left( {x\sqrt x - 1} \right) = 0\\ \Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\\sqrt x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array}\)
Thể tích V của một vật tròn xoay tạo thành khi quay quanh hình phẳng (H) giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) quanh trục Ox là:
\(V=~\pi \int_{0}^{1}{\left| {{\left( {{x}^{2}} \right)}^{2}}-{{\left( \sqrt{x} \right)}^{2}} \right|dx=}\pi \int_{0}^{1}{\left| {{x}^{4}}-x \right|dx=}-\pi \int_{0}^{1}{({{x}^{4}}-x)dx=}=-\pi \left. \left( \dfrac{{{x}^{5}}}{5}-\dfrac{{{x}^{2}}}{2} \right)\,\, \right|_{o}^{1}=\dfrac{3\pi }{10}\)
Trong mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường \(4y={{x}^{2}}\) và \(y=x\). Thể tích của vật thể tròn xoay khi quay hình (H) quanh trục hoành một vòng bằng
Phương trình hoành độ giao điểm của \(4y={{x}^{2}}\) và \(y=x\) là: \(\frac{{{x}^{2}}}{4}=x\Leftrightarrow {{x}^{2}}-4x=0\Leftrightarrow \left[ \begin{align} x=0 \\ x=4 \\ \end{align} \right.\)
\(V=\pi \int\limits_{0}^{4}{\left| \left( \frac{{{x}^{2}}}{4} \right)^2-{{x}^{2}} \right|dx}=\frac{\pi }{16}\int\limits_{0}^{4}{\left| {{x}^{4}}-16{{x}^{2}} \right|dx=}-\frac{\pi }{16}\int\limits_{0}^{4}{\left( {{x}^{4}}-16{{x}^{2}} \right)dx=-}\frac{\pi }{16}\left. \left( \frac{{{x}^{5}}}{5}-\frac{16}{3}{{x}^{3}} \right) \right|_{0}^{4}=-\frac{\pi }{16}\left( \frac{{{4}^{5}}}{5}-\frac{16}{3}{{.4}^{3}} \right)=\frac{128}{15}\pi \)
Gọi D là phần hình phẳng giới hạn bởi các đường thẳng \(x = - 1,\,\,y = 0,\,\,y = {x^3}\). Thể tích khối tròn xoay tạo nên khi quay D quanh trục Ox bằng:
Xét phương trình hoành độ giao điểm \({x^3} = 0 \Leftrightarrow x = 0\).
Vậy \(V = \pi \int\limits_{ - 1}^0 {\left| {{x^6}} \right|dx} = \pi \left. {\frac{{{x^7}}}{7}} \right|_{ - 1}^0 = \pi \left( {0 + \frac{1}{7}} \right) = \frac{\pi }{7}\)
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục \(Ox\) hình phẳng giới hạn bởi các đường \(y = 0,y = \sqrt x ,y = x - 2.\)
Hoành độ giao điểm của \(\left( C \right)\) và \(d\) là nghiệm phương trình: \(\sqrt x = x - 2 \Leftrightarrow x = 4.\)
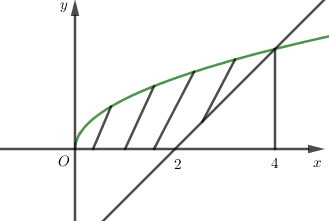
Khi đó, thể tích khối tròn xoay cần tính là \(V = \pi \int\limits_0^4 {{{\left( {\sqrt x } \right)}^2}\,{\rm{d}}x} - \pi \int\limits_2^4 {{{\left( {x - 2} \right)}^2}\,{\rm{d}}x} = \frac{{16\pi }}{3}.\)

