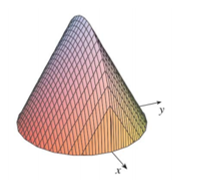
Cho vật thể có mặt đáy là hình tròn bán kính bằng $1$ (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ \(\left( -1\le x\le 1 \right)\) thì thiết diện là một tam giác đều. Tính thể tích $V$ của vật thể đó.
Trả lời bởi giáo viên
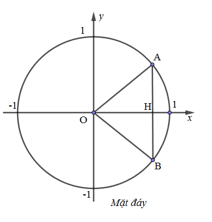
Ở mặt đáy, tam giác $OHB$ vuông tại $H$ \(\Rightarrow HB=\sqrt{O{{B}^{2}}-O{{H}^{2}}}=\sqrt{1-{{x}^{2}}}\)
\(\Rightarrow AB=2\sqrt{1-{{x}^{2}}}\)
Diện tích của mặt cắt khi cắt vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ \(\left( -1\le x\le 1 \right)\)là:
\(S(x)=\frac{A{{B}^{2}}\sqrt{3}}{4}=\frac{{{\left( 2\sqrt{1-{{x}^{2}}} \right)}^{2}}.\sqrt{3}}{4}=\sqrt{3}(1-{{x}^{2}})\)
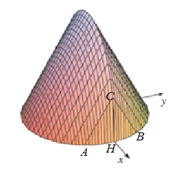
Thể tích cần tìm : \(V=\int\limits_{-1}^{1}{S(x)dx}=\int\limits_{-1}^{1}{\sqrt{3}(1-{{x}^{2}})dx}=\sqrt{3}\left. \left( x-\frac{1}{3}{{x}^{3}} \right) \right|_{-1}^{1}=\sqrt{3}.\frac{4}{3}=\frac{4\sqrt{3}}{3}\)
Hướng dẫn giải:
Ứng dụng tích phân vào tính thể tích khối tròn xoay \(V=\int\limits_{a}^{b}{S(x)dx}\), trong đó \(S(x)\)là diện tích của mặt cắt tại mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x.