Câu hỏi:
3 năm trước
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục \(Ox\) hình phẳng giới hạn bởi các đường \(y = 0,y = \sqrt x ,y = x - 2.\)
Trả lời bởi giáo viên
Đáp án đúng: b
Hoành độ giao điểm của \(\left( C \right)\) và \(d\) là nghiệm phương trình: \(\sqrt x = x - 2 \Leftrightarrow x = 4.\)
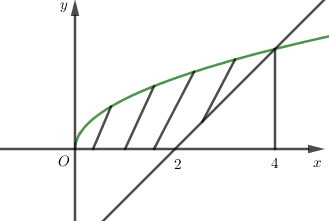
Khi đó, thể tích khối tròn xoay cần tính là \(V = \pi \int\limits_0^4 {{{\left( {\sqrt x } \right)}^2}\,{\rm{d}}x} - \pi \int\limits_2^4 {{{\left( {x - 2} \right)}^2}\,{\rm{d}}x} = \frac{{16\pi }}{3}.\)
Hướng dẫn giải:
Vẽ hình, xác định hình phẳng giới hạn bởi ba đồ thị hàm số và áp dụng công thức tính thể tích khối tròn xoay \(V = \pi \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \)