Khảo sát sự biến thiên và vẽ đồ thị của hàm đa thức (hàm bậc bốn trùng phương)

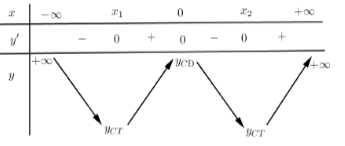
Từ bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to  \pm \infty } y =  + \infty$ nên $a > 0$.

Hàm bậc bốn trùng phương có $a > 0$ và $3$ điểm cực trị thì có $1$ điểm cực đại và $2$ điểm cực tiểu.

Nếu hàm số bậc bốn trùng phương có $y' = 0$ có $3$ nghiệm phân biệt thì nó có $3$ điểm cực trị.

Hàm số bậc bốn trùng phương luôn có ít nhất $1$ điểm cực trị.

Dễ thấy hàm số bậc bốn trùng phương có cực đại, cực tiểu thì ${y_{CT}} < {y_{CD}}$ nên nếu ${y_{CT}} > 0$ thì ${y_{CD}} > 0$.

Ta có: $y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right)$.

Hàm số có 1 cực trị $\Leftrightarrow y' = 0$ có $3$ nghiệm phân biệt $\Leftrightarrow 2a{x^2} + b = 0$ có $2$ nghiệm phân biệt khác $0$$\Leftrightarrow ab < 0$.

Đồ thị hàm bậc 4 trùng phương luôn cắt trục tung tại điểm $\left( {0;c} \right)$ chính là cực trị của đồ thị hàm số.

Ngoài ra, đồ thị hàm số bậc 4 trùng phương cũng có thể không cắt $Ox$ nên A sai.

Đồ thị nhận trục tung làm trục đối xứng nên C sai.

Đồ thị không có tâm đối xứng nên D sai.

Đồ thị hàm số bậc bốn trùng phương có ba cực trị và hệ số $a > 0$ có dạng:

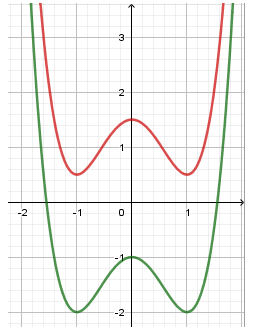
Quan sát đồ thị ta thấy nếu ${y_{CD}} < 0$ thì đồ thị hàm số cắt trục hoành tại đúng $2$ điểm phân biệt.

Hàm số chỉ có 1 cực trị thì $y' = 0$ có 1 nghiệm $\Leftrightarrow ab \ge 0$, khi đó đồ thị có dạng:

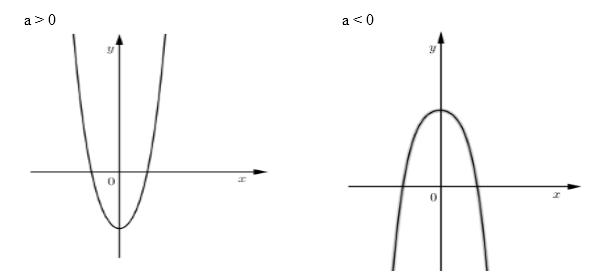
Trong hai trường hợp trên ta thấy nếu đồ thị hàm số nằm hoàn toàn phía dưới trục hoành thì chỉ xảy ra trường hợp $a < 0$, do đó $b \le 0$ và điểm cực tiểu $\left( {0;c} \right)$ cũng phải nằm phía dưới trục hoành hay $c < 0$.

Hàm số $y = a{x^4} + b{x^2} + c$ có $a < 0,b = 0,c > 0$ nên có $1$ cực trị và chính là điểm cực đại.

Đồ thị có dạng như sau:

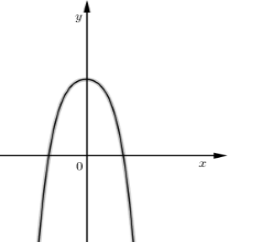
Quan sát đồ thị ta thấy:

- Đồ thị hàm số cắt trục hoành tại $2$ điểm phân biệt nên A đúng, B sai.

- Đồ thị hàm số chỉ có $1$ điểm cực đại và nó nằm ở phía trên của trục hoành nên C đúng.

- Đồ thị hàm số đi qua điểm $\left( {0;c} \right)$ và $c > 0$ nên nó không đi qua gốc tọa độ.

+ TH1: $a > 0,b < 0$, đồ thị có dạng:

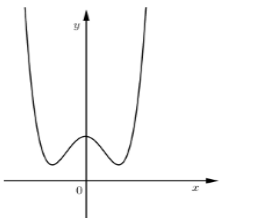
Khi đó, đồ thị hàm số có $2$ điểm chung với $Ox$ nếu điểm cực đại $\left( {0;c} \right)$ nằm hoàn toàn phía dưới $Ox$ hay $c < 0$.

Do đó $c < 0$ .

+TH2: $a > 0,b \ge 0$, đồ thị có dạng:

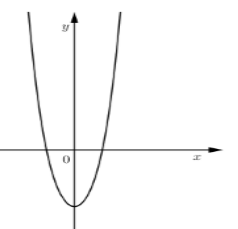
Khi đó, đồ thị hàm số có $2$ điểm chung với $Ox$ nếu điểm cực tiểu $\left( {0;c} \right)$ nằm hoàn toàn phía dưới $Ox$ hay $c < 0$.

Vậy trong cả hai trường hợp trên ta đều thấy, nếu $c < 0$ thì đồ thị hàm số sẽ có hai giao điểm với $Ox$.

Hàm số bậc bốn luôn có $\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  - \infty } y$.

Hàm số bậc bốn trùng phương xác định trên $R$.

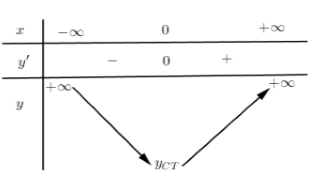
Hàm số đồng biến trên $\left( {0; + \infty } \right)$ và nghịch biến trên $\left( { - \infty ;0} \right)$ hay hàm số tăng trên $\left( {0; + \infty } \right)$ và giảm trên $\left( { - \infty ;0} \right)$

Hàm số $y = \left( {2\sqrt 2  - 3} \right){x^4} + \sqrt 2 {x^2} - 1$ có $a = 2\sqrt 2  - 3 < 0$ nên$\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \left( {\left( {2\sqrt 2  - 3} \right){x^4} + \sqrt 2 {x^2} - 1} \right) =  - \infty$

Hàm số bậc bốn trùng phương xác định trên $\mathbb{R}$ nên A đúng.

Vì $a > 0$ nên $\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  - \infty } y =  + \infty$.

Hàm số $y = \sqrt 2 {x^4} - {x^2}$ có $a = \sqrt 2  > 0$ nên $\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt 2 {x^4} - {x^2}} \right) =  + \infty$

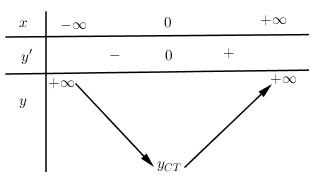
Hàm số đồng biến trên $\left( {0; + \infty } \right)$ và nghịch biến trên $\left( { - \infty ;0} \right)$.

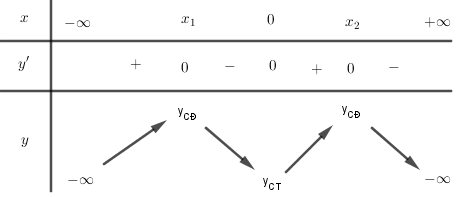
Từ bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to  \pm \infty } y =  - \infty$ nên $a < 0$.