Trả lời bởi giáo viên
Đáp án đúng: b
Hàm số y=ax4+bx2+c có a<0,b=0,c>0 nên có 1 cực trị và chính là điểm cực đại.
Đồ thị có dạng như sau:
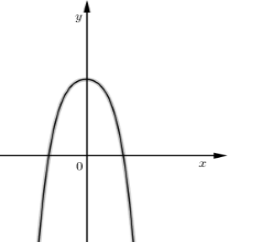
Quan sát đồ thị ta thấy:
- Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt nên A đúng, B sai.
- Đồ thị hàm số chỉ có 1 điểm cực đại và nó nằm ở phía trên của trục hoành nên C đúng.
- Đồ thị hàm số đi qua điểm (0;c) và c>0 nên nó không đi qua gốc tọa độ.
Hướng dẫn giải:
Vẽ dạng đồ thị hàm số thỏa mãn điều kiện đề bài và xét tính đúng sai của từng đáp án.