Trong không gian \(Oxyz\), cho điểm \(A\left( {3;2;0} \right)\) và đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}\). Đường thẳng đi qua \(A\), vuông góc và cắt \(\Delta \) có phương trình là:
Gọi đường thẳng cần tìm là \(d\). Gọi \(B = d \cap \Delta \).
Vì \(B \in \Delta \Rightarrow B\left( {1 + t;\,\,t;\,\, - 1 + 2t} \right)\).
Ta có: \(\overrightarrow {AB} = \left( {t - 2;\,\,t - 2;\,\,2t - 1} \right)\).
Đường thẳng \(\Delta \) có 1 VTCP là \(\overrightarrow {{u_\Delta }} = \left( {1;1;2} \right)\).
Vì \(d \bot \Delta \) nên \(\overrightarrow {AB} \bot \overrightarrow {{u_\Delta }} \).
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} .\overrightarrow {{u_\Delta }} = 0\\ \Leftrightarrow 1.\left( {t - 2} \right) + 1.\left( {t - 2} \right) + 2.\left( {2t - 1} \right) = 0\\ \Leftrightarrow 6t - 6 = 0 \Leftrightarrow t = 1\end{array}\)
\( \Rightarrow B\left( {2;1;1} \right)\) và \(\overrightarrow {AB} = \left( { - 1; - 1;1} \right)\).
Vậy đường thẳng \(d\) đi qua \(A\left( {3;2;0} \right)\) và có 1 VTCP \(\overrightarrow u = - \overrightarrow {AB} = \left( {1;1; - 1} \right)\) có phương trình là: \(\dfrac{{x - 3}}{1} = \dfrac{{y - 2}}{1} = \dfrac{z}{{ - 1}}\).
Trong không gian \(Oxyz,\) vị trí tương đối giữa hai đường thẳng \(\left( {{d_1}} \right):\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = - 4 - 3t\\z = 3 + 2t\end{array} \right.\) và \(\left( {{d_2}} \right):\,\,\,\dfrac{{x - 5}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 3}}\) là:
Ta có: \(\left( {{d_1}} \right):\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = - 4 - 3t\\z = 3 + 2t\end{array} \right.\) có VTCP là: \(\overrightarrow {{u_1}} = \left( {2; - 3;\,\,2} \right)\) và đi qua \({M_1}\left( {1; - 4;\,\,3} \right)\)
\(\left( {{d_2}} \right):\,\,\,\dfrac{{x - 5}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 3}}\) có VTCP là: \(\overrightarrow {{u_2}} = \left( {3;\,\,2; - 3} \right)\) và đi qua \({M_2}\left( {5; - 1;\,\,2} \right)\)
\( \Rightarrow \left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right] = \left( {5;\,\,12;\,\,13} \right) \ne \overrightarrow 0 \) \( \Rightarrow \) \({d_1}\) và \({d_2}\) cắt nhau hoặc chéo nhau.
Ta có: \(\overrightarrow {{M_1}{M_2}} = \left( {4;\,\,3;\, - 1} \right)\)
\( \Rightarrow \left[ {\overrightarrow {{u_1}} ,\,\,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = 4.5 + 3.12 - 13 = 43 \ne 0\)
\( \Rightarrow {d_1}\) và \({d_2}\) chéo nhau.
Trong không gian với hệ trục tọa độ \(\left( {Oxyz} \right)\). Cho đường thẳng \(\left( d \right):\dfrac{{x - 4}}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{1}\). Đường thẳng \(\left( d_1 \right)\) đi qua điểm \(A\left( {0;1;2} \right),\)\(\left( {{d_1}} \right)\) cắt và vuông góc với \(\left( d \right).\)\(\left( {{d_1}} \right)\) có phương trình là
Gọi mặt phẳng \(\left( P \right)\)là mặt phẳng đi qua \(A\left( {0;1;2} \right)\) và vuông góc với đường thẳng \(\left( d \right):\dfrac{{x - 4}}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{1}\)
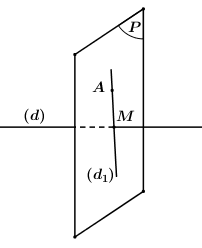
Khi đó mặt phẳng \(\left( P \right)\) có 1 vectơ pháp tuyến là \(\overrightarrow n = \overrightarrow {{u_d}} = \left( {2; - 1;1} \right)\).
\( \Rightarrow \) Phương trình mặt phẳng \(\left( P \right)\) là: \(2\left( {x - 0} \right) - 1\left( {y - 1} \right) + 1\left( {z - 2} \right) = 0\) \( \Leftrightarrow 2x - y + z - 1 = 0\).
Gọi \(M = d \cap \left( P \right)\).
\(\begin{array}{l}M \in d \Rightarrow M\left( {4 + 2t;\,\,1 - t;\,\,t} \right)\\M \in \left( P \right):\,\,2x - y + z - 1 = 0\\ \Rightarrow 2\left( {4 + 2t} \right) - \left( {1 - t} \right) + t - 1 = 0\\ \Leftrightarrow 6t + 6 = 0 \Leftrightarrow t = - 1\\ \Rightarrow M\left( {2;2; - 1} \right)\end{array}\)
Khi đó đường thẳng \(\left( {{d_1}} \right)\) đi qua \(A\left( {0;1;2} \right),\,\,M\left( {2;2; - 1} \right)\) nhận \(\overrightarrow {AM} = \left( {2;1; - 3} \right)\) là 1 VTCP.
Vậy phương trình đường thẳng \({d_1}\) là: \(\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{{ - 3}}\).
Trong không gian Oxyz, cho ba điểm \(A(2; - 2;3),B(1;3;4)\) và \(C(3; - 1;5)\). Đường thẳng đi qua \(A\) và song song với $B C$ có phương trình là:
Ta có \(\overrightarrow {BC} (2; - 4;1)\) nên phương trình đường thẳng đi qua \(A\) và song song với $B C$ là: \(\dfrac{{x - 2}}{2} = \dfrac{{y + 2}}{{ - 4}} = \dfrac{{z - 3}}{1}.\)
Trong không gian \(Oxyz,\) cho hai đường thẳng \({\Delta _1}:\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y + 2}}{1} = \dfrac{{z - 3}}{2}\) và \({\Delta _2}:\,\,\dfrac{{x + 3}}{1} = \dfrac{{y - 1}}{1} = \dfrac{{z + 2}}{{ - 4}}.\) Góc giữa hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) bằng:
Ta có: \({\Delta _1}\) có VTCP là: \(\overrightarrow {{u_1}} = \left( { - 2;\,\,1;\,\,2} \right),\,\,\Delta \) có VTCP là: \(\overrightarrow {{u_2}} = \left( {1;\,\,1; - 4} \right).\)
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\left( {{\Delta _1};\,\,{\Delta _2}} \right)\) ta có:
\(\begin{array}{l}\cos \alpha = \dfrac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \dfrac{{\left| { - 2.1 + 1.1 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + 1 + {2^2}} .\sqrt {1 + 1 + {{\left( { - 4} \right)}^2}} }} = \dfrac{9}{{3.3\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\\ \Rightarrow \alpha = {45^0}.\end{array}\)
Trong không gian \(Oxyz,\) cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = - 1 + t\\y = 3 + 2t\\z = - 1 - t\end{array} \right.\) và\({d_2}:\left\{ \begin{array}{l}x = 7 + 3s\\y = 1 - s\\z = 5 - s\end{array} \right.\) . Khoảng cách giữa hai đường thẳng đã cho bằng
Ta có đường thẳng \({d_1}\) đi qua \({M_1}\left( { - 1;3; - 1} \right)\) và nhận \(\overrightarrow {{u_1}} = \left( {1;2; - 1} \right)\) làm VTCP
Đường thẳng \({d_2}\) đi qua \({M_2}\left( {7;1;5} \right)\) và nhận \(\overrightarrow {{u_2}} = \left( {3; - 1; - 1} \right)\) làm VTCP
Xét \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( { - 3; - 2; - 7} \right);\,\overrightarrow {{M_1}{M_2}} = \left( {8; - 2;6} \right)\) \( \Rightarrow \overrightarrow {{M_1}{M_2}} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( { - 3} \right).8 + \left( { - 2} \right).\left( { - 2} \right) + \left( { - 7} \right).6 = - 62 \ne 0\)
Nên \({d_1};{d_2}\) chéo nhau.
Suy ra khoảng cách \(d\left( {{d_1};{d_2}} \right) = \dfrac{{\left| {\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right|}} = \dfrac{{\left| { - 62} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 7} \right)}^2}} }} = \sqrt {62} \)
Cho \(d,d'\) là các đường thẳng có VTCP lần lượt là \(\overrightarrow u ,\overrightarrow {u'} \). Nếu \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \overrightarrow 0 \) thì:
Ta có:
Nếu \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \overrightarrow 0 \) thì \(\overrightarrow u \) cùng phương \(\overrightarrow {u'} \) nên \(d//d'\) hoặc \(d \equiv d'\).
Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng
\({d_1}:\left\{ \begin{array}{l}x = - 1 + 2t\\y = - t\\z = 1 + t\end{array} \right.\) và \({d_2}:\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y + 1}}{1} = \dfrac{{z - 2}}{{ - 1}}\).
Vị trí tương đối của \({d_1}\) và \({d_2}\) là:
Đường thẳng \({d_1}\) đi qua \({M_1}\left( { - 1;0;1} \right)\) và có VTCP \(\overrightarrow {{u_1}} = \left( {2; - 1;1} \right)\).
Đường thẳng \({d_2}\) đi qua \({M_2}\left( {1; - 1;2} \right)\) và có VTCP \(\overrightarrow {{u_2}} = \left( { - 2;1; - 1} \right)\).
Ta có \(\dfrac{2}{{ - 2}} = \dfrac{{ - 1}}{1} = \dfrac{1}{{ - 1}}\) nên \(\overrightarrow {{u_1}} //\overrightarrow {{u_2}} \). \(\left( 1 \right)\)
\(\dfrac{{ - 1 - 1}}{{ - 2}} = \dfrac{{0 + 1}}{1} = \dfrac{{1 - 2}}{{ - 1}}\) nên \(M \in {d_2}\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \({d_1}\) và \({d_2}\) trùng nhau.
Khi xét hệ phương trình giao hai đường thẳng, nếu hệ có nghiệm duy nhất thì:
Nếu hệ phương trình giao điểm hai đường thẳng có nghiệm duy nhất thì hai đường thẳng cắt nhau.
Khi xét hệ phương trình giao điểm hai đường thẳng, nếu hệ vô nghiệm và hai véc tơ \(\overrightarrow u ,\overrightarrow {u'} \) cùng phương thì hai đường thẳng:
Nếu hệ phương trình giao điểm hai đường thẳng vô nghiệm thì \(d\) và \(d'\) không có điểm chung thì hoặc song song hặc chéo nhau.
Hơn nữa \(\overrightarrow u ,\overrightarrow {u'} \) cùng phương thì hai đường thẳng song song.
Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng
\({d_1}:\dfrac{x}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{{ - 3}}\) và \({d_2}:\left\{ \begin{array}{l}x = 2t\\y = - 3 - t\\z = 0\end{array} \right.\). Mệnh đề nào sau đây đúng:
Đường thẳng \({d_1}\) qua \({M_1}\left( {0;0;2} \right)\) và có VTCP \(\overrightarrow {{u_1}} = \left( {1;2; - 3} \right)\),
\({d_2}\) qua \({M_2}\left( {0; - 3;0} \right)\) và có VTCP \(\overrightarrow {{u_2}} = \left( {2; - 1;0} \right)\).
+) \(\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 2 - 2 = 0 \Rightarrow {d_1} \bot {d_2}\)\(\left( 1 \right)\)
+) \(\left[ {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right] = \left( { - 3; - 6; - 5} \right),\,\,\,\overrightarrow {{M_1}{M_2}} = \left( {0; - 3; - 2} \right) \Rightarrow \overrightarrow {{M_1}{M_2}} .\left[ {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right] = 18 + 10 \ne 0\)
Vậy \({d_1}\) vuông góc \({d_2}\) và không cắt nhau.
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x + 2}}{2} = \dfrac{y}{{ - 1}} = \dfrac{{z + 1}}{2}\). Trong các đường thẳng sau, đường thẳng nào song song với \(d\)?
Đường thẳng \({d_3}\) qua \(M\left( { - 2; - 3;1} \right)\) và có VTCP \({\overrightarrow u _{_3}} = \left( { - 4;2; - 4} \right)\).
Đường thẳng \(d\) có VTCP \({\overrightarrow u _{_d}} = \left( {2; - 1;2} \right)\). Ta có \({\overrightarrow u _{_3}} = - 2\left( {2; - 1;2} \right) = - 2{\overrightarrow u _{_d}}\).
Thay tọa độ điểm \(M\left( { - 2; - 3;1} \right)\) vào \(d:\dfrac{{ - 2 + 2}}{2} = \dfrac{{ - 3}}{{ - 1}} = \dfrac{{1 + 1}}{2}\) không thỏa mãn.
Cho hình vẽ dưới đây, công thức nào không dùng để tính khoảng cách từ điểm \(A\) đến đường thẳng \(d'\)?
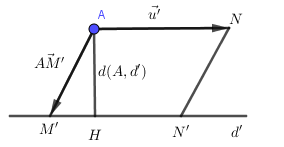
Quan sát hình vẽ ta thấy: \({S_{AM'N'N}} = \left| {\left[ {\overrightarrow {AN} ,\overrightarrow {AM'} } \right]} \right| = AH.\left| {\overrightarrow {M'N'} } \right| \Rightarrow AH = \dfrac{{\left| {\left[ {\overrightarrow {AN} ,\overrightarrow {AM'} } \right]} \right|}}{{\left| {\overrightarrow {M'N'} } \right|}}\) nên các đáp án A, B, D đều đúng.
Đáp án C sai vì \(\dfrac{{\left| {\left[ {\overrightarrow {AM'} ,\overrightarrow {u'} } \right]} \right|}}{{\left| {\overrightarrow {NN'} } \right|}} = \dfrac{{{S_{AM'N'N}}}}{{\left| {\overrightarrow {NN'} } \right|}} = d\left( {A,NN'} \right)\)
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + 2t\\y = 2\\z = - t\end{array} \right.\).
Khoảng cách từ \(A\left( {0; - 1;3} \right)\) đến đường thẳng \(\Delta \) bằng:
Gọi \(M\left( {1 + 2t;2; - t} \right) \in \Delta \).
Ta có \(A{M^2} = {\left( {1 + 2t} \right)^2} + 9 + {\left( { - t - 3} \right)^2} = 5{\left( {t + 1} \right)^2} + 14 \ge 14.\)
Suy ra \(d\left[ {A,\Delta } \right] = A{M_{\min }} \Leftrightarrow t = - 1 \Leftrightarrow AM = \sqrt {14} .\)
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{1} = \dfrac{{z - 1}}{2}\). Khoảng cách từ $A\left( {1;0;3} \right)$ đến \(\Delta \) bằng:
Đường thẳng \(\Delta \) đi qua \(M\left( {1; - 1;1} \right)\) và có VTCP \(\overrightarrow {{u_\Delta }} = \left( {2;1;2} \right)\).
Ta có \(\overrightarrow {AM} = \left( {0; - 1; - 2} \right)\), suy ra \(\left[ {\overrightarrow {AM} ,\overrightarrow {{u_\Delta }} } \right] = \left( {0; - 4;2} \right)\).
Khi đó \(d\left( {A,\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow {AM} ,\overrightarrow {{u_\Delta }} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}} = \dfrac{{2\sqrt 5 }}{3}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm $A\left( {1; - 1;0} \right),\,\,B\left( {1;0; - 2} \right),$ $C\left( {3; - 1; - 1} \right)$. Tính khoảng cách từ điểm $A$ đến đường thẳng $BC$.
Ta có $\overrightarrow {AB} = \left( {0;1; - 2} \right)$ và $\overrightarrow {BC} = \left( {2; - 1;1} \right)$. Suy ra $\left[ {\overrightarrow {AB} ,\overrightarrow {BC} } \right] = \left( { - 1; - 4; - 2} \right)$.
Khi đó \(d\left( {A,BC} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {BC} } \right]} \right|}}{{\left| {\overrightarrow {BC} } \right|}} = \dfrac{{\sqrt {21} }}{{\sqrt 6 }} = \dfrac{{\sqrt {14} }}{2}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\left( {2; - 1;1} \right)\) và hai đường thẳng \({d_1}:\dfrac{{x - 2}}{1} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z - 1}}{2}\), \({d_2}:\dfrac{{x - 2}}{2} = \dfrac{{y + 3}}{1} = \dfrac{{z - 1}}{{ - 1}}\). Đường thẳng \(\Delta \) cắt \({d_1}\), \({d_2}\) lần lượt tại \(A\) và \(B\) sao cho \(M\) là trung điểm của \(AB\) có phương trình:
Do \(A = \Delta \cap {d_1}\) suy ra \(A\in \Delta\) nên \(A\left( {2 + t;1 - 2t;1 + 2t} \right)\).
Vì \(M\) là trung điểm \(AB\), suy ra:
$\begin{array}{l}
\left\{ \begin{array}{l}
{x_M} = \frac{{{x_A} + {x_B}}}{2}\\
{y_M} = \frac{{{y_A} + {y_B}}}{2}\\
{z_M} = \frac{{{z_A} + {z_B}}}{2}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{x_B} = 2{x_M} - {x_A}\\
{y_B} = 2{y_M} - {y_A}\\
{z_B} = 2{z_M} - {z_A}
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
{x_B} = 2.2 - \left( {2 + t} \right) = 2 - t\\
{y_B} = 2.\left( { - 1} \right) - \left( {1 - 2t} \right) = - 3 + 2t\\
{z_B} = 2.1 - \left( {1 + 2t} \right) = 1 - 2t
\end{array} \right.\\
\Rightarrow B\left( { - t + 2;2t - 3; - 2t + 1} \right)
\end{array}$
Theo giả thiết, \(B \in {d_2}\) nên \(\dfrac{{ - t + 2 - 2}}{2} = \dfrac{{2t - 3 + 3}}{1} = \dfrac{{ - 2t + 1 - 1}}{{ - 1}} \)
\(\Leftrightarrow t = 0 \Rightarrow \left\{ \begin{array}{l}A\left( {2;1;1} \right)\\B\left( {2; - 3;1} \right)\end{array} \right.\)
Đường thẳng \(\Delta \) đi qua hai điểm \(A\left( {2;1;1} \right)\), \(B\left( {2; - 3;1} \right)\) nên \(\Delta :\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 1\end{array} \right.\)
Khoảng cách giữa hai đường thẳng \({d_1}:\dfrac{x}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{z}{3},{d_2}:\dfrac{{x + 1}}{1} = \dfrac{y}{3} = \dfrac{{z + 1}}{{ - 2}}\) là:
Đường thẳng \({d_1}\) đi qua điểm \({M_1}\left( {0;1;0} \right)\) và có VTCP \(\overrightarrow {{u_1}} = \left( {2; - 1;3} \right)\).
Đường thẳng \({d_2}\) đi qua điểm \({M_2}\left( { - 1;0; - 1} \right)\) và có VTCP \(\overrightarrow {{u_2}} = \left( {1;3; - 2} \right)\).
Khi đó \(\overrightarrow {{M_1}{M_2}} = \left( { - 1; - 1; - 1} \right),\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}\begin{array}{l} - 1\\3\end{array}&\begin{array}{l}3\\ - 2\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}3\\ - 2\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l} - 1\\3\end{array}\end{array}} \right|} \right) = \left( { - 7;7;7} \right)\)
Vậy \(d\left( {{d_1},{d_2}} \right) = \dfrac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}} = \dfrac{{\left| {\left( { - 7} \right).\left( { - 1} \right) + 7.\left( { - 1} \right) + 7.\left( { - 1} \right)} \right|}}{{\sqrt {{7^2} + {7^2} + {7^2}} }} = \dfrac{1}{{\sqrt 3 }}\)
Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {1;0;2} \right)\) và đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}\). Viết phương trình đường thẳng \(\Delta \) đi qua \(A,\) vuông góc và cắt \(d\).
Gọi \(B = \Delta \cap d\), suy ra \(B \in d\) nên $B\left( {1 + t;t; - 1 + 2t} \right)$.
Khi đó \(\Delta \) có VTCP là $\overrightarrow {AB} = \left( {t;t;2t - 3} \right)$. Đường thẳng \(d\) có VTCP \(\overrightarrow {{u_d}} = \left( {1;1;2} \right)\).
Theo đề bài: \(\Delta \bot d \Leftrightarrow \overrightarrow {AB} .\overrightarrow {{u_d}} = t + t + 4t - 6 = 0 \Leftrightarrow t = 1 \Rightarrow B\left( {2;1;1} \right)\).
Đường thẳng \(\Delta \) cần tìm đi qua hai điểm \(A,{\rm{ }}B\) nên \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z - 2}}{{ - 1}}\).
Trong không gian với hệ tọa độ Oxyz , tính góc giữa hai đường thẳng \({d_1}:\dfrac{x}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 1}}{2}\) và \({d_2}:\dfrac{{x + 1}}{{ - 1}} = \dfrac{y}{1} = \dfrac{{z - 3}}{1}\)
\({d_1}\) có vecto chỉ phương \(\overrightarrow {{u_1}} = \left( {1; - 1;2} \right)\); \({d_2}\) có vecto chỉ phương \(\overrightarrow {{u_2}} = \left( { - 1;1;1} \right)\)
\(\cos \left( {\widehat {{d_1},{d_2}}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right| = \dfrac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \dfrac{{\left| {1.( - 1) + ( - 1).1 + 2.1} \right|}}{{\sqrt {1 + 1 + 1} .\sqrt {1 + 1 + {2^2}} }} = 0 \Rightarrow \left( {\widehat {{d_1},{d_2}}} \right) = {90^0}\)

